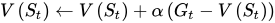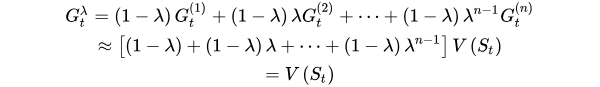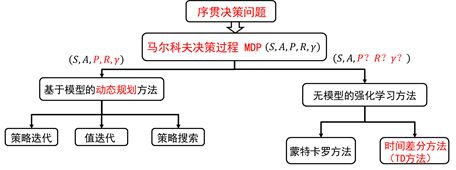
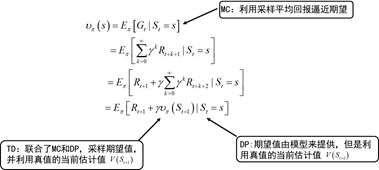
时间差分方法结合了蒙特卡罗的采样方法(即做试验)和动态规划方法的bootstrapping(利用后继状态的值函数估计当前值函数)。
蒙特卡罗要等到实验结束才能有Gt,太慢。
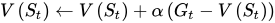

其中
Rt+1+γV(St+1)称为TD目标,与(4.2)中的
Gt相对应,两者不同之处是TD目标利用了bootstrapping方法估计当前值函数。
δt=Rt+1+γV(St+1)−V(St)称为TD偏差。
比较:
蒙特卡罗的方法使用的是值函数最原始的定义,该方法利用所有回报的累积和估计值函数。DP方法和TD方法则利用一步预测方法计算当前状态值函数。其共同点是利用了bootstrapping方法,不同的是,DP方法利用模型计算后继状态,而TD方法利用试验得到后继状态。
TD如何利用实验得到后续状态?
- 优点:
蒙特卡罗方法每次得到的G_t 值要等到最终状态出现,在这个过程中要经历很多随机的状态和动作,因此每次得到的G_t随机性很大,所以尽管期望等于真值,但方差无穷大。
具体实现:
在更新当前值函数时,用到了下一个状态的值函数。那么我们可以以此推理,能不能利用后继第二个状态的值函数来更新当前状态的值函数呢?
答案是肯定的,那么如何利用公式计算呢?
我们用
Gt(1)=Rt+1+γV(St+1)表示TD目标,
则利用第二步值函数来估计当前值函数可表示为:
Gt(2)=Rt+1+γRt+2+γ2V(St+1)
以此类推,利用第n步的值函数更新当前值函数可表示为:
Gt(n)=Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n)
对这n个估计值利用加权的方法进行融合一下呢?这就是
TD(λ)的方法。
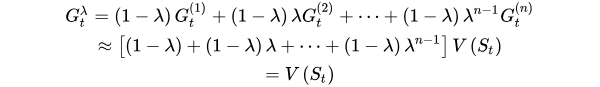
V(St)←V(St)+α(Gt(λ)−V(St))(4.4)
其中
Gtλ=(1−λ)n=1∑∞λn−1Gt(n),而
Gt(n)=Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n)
但是,
Gtλ 的计算用到了将来时刻的值函数,因此需要等到整个试验结束之后。这跟蒙塔卡罗方法相似.

假设当前状态为
st,TD偏差为
δt ,那么
st−1处的值函数更新应该乘以一个衰减因子
γλ ,状态
st−2 处的值函数更新应该乘以
(γλ)2 ,以此类推。
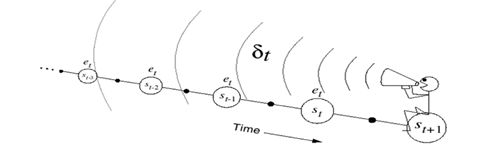
Sarsa既是这种算法。