梯度下降（gradient descent）原理

目标：解决多变量函数的最优化问题

例如神经网络中的损失函数（loss function）：
$C(w,b)=\frac{1}{2n}\sum_{x}\|y(x)-a\|^2$

其中 $w$和 $b$为网络的参数， $x$为训练样本， $n$为训练样本的数目， $y(x)$为网络的期望输出， $a$为网络的实际输出， $a$是 $x,w,b$的函数。
为了让网络的输出尽可能接近期望输出，即求令损失函数最小化的网络参数 $w^*$和 $b^*$：
$\min \limits_{w,b} \frac{1}{2n}\sum_{x}\|y(x)-a\|^2$

我们可以采用梯度下降（gradient descent）求解该问题。

梯度下降法

1. 为什么用梯度下降法?

• 对于多变量问题，常用的微积分解法效果有限；
• 对于神经网络而言，常常包含大量的变量，采用微积分最小化的方法失效

2. 梯度下降法的灵感来源

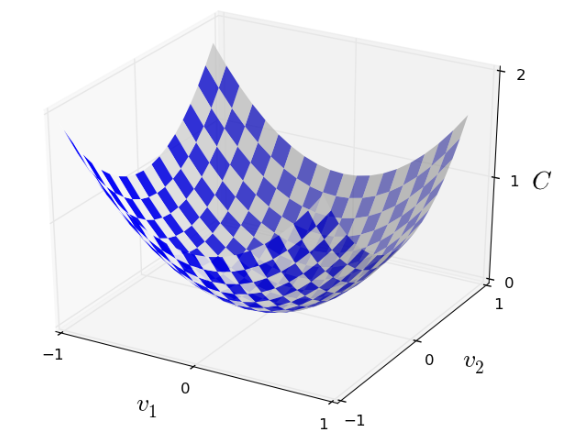
我们假设 $C(v)$是包含两个变量 $v_1,v_2$的函数，大概长这样

为了找到 $C(v)$的最小值，我们可以将 $C(v)$想象成一个山谷，假设某一个位置处有一个球沿着斜坡往下滚，则最后这个球一定会到达谷底。根据这一思想，我们可以随机选取一个起始点，然后模拟球往下滚的过程，最终找到 $C(v)$的最小值点（即谷底）。

为了实现这一过程，我们先假设沿 $v_1$方向移动 $\Delta{v_1}$，沿 $v_2$方向移动 $\Delta{v_2}$，我们可以计算出 $C(v)$的变化：
$\Delta{C}\approx\frac{\partial C}{\partial v_1}\Delta{v_1}+\frac{\partial C}{\partial v_2}\Delta v_2$

假设我们选择 $\Delta v_1$和 $\Delta v_2$使得 $\Delta C<0$，重复这一过程，就能让球滚到谷底（求得 $C$的最小值点）。现在的重点是我们如何选择这样的 $\Delta v=(\frac{\partial C}{\partial v_1},\frac{\partial C}{\partial v_2})^T$使得 $\Delta C<0$呢？

3. 梯度下降原理

这里我们首先来改写一下 $\Delta C$的公式。令
$\Delta C\approx \nabla C \cdot \Delta v$

其中 $\nabla C \equiv (\frac{\partial C}{\partial v_1},\frac{\partial C}{\partial v_2})^T$。采用逐元素乘法（向量内积）。 $\nabla C$ 被称作 gradient vector，用于描述 $C$相对于 $v$的变化率。

为了选取合适的 $\Delta v$使得 $\Delta C<0$，我们可以选取
$\Delta v=-\eta \nabla C$

where $\eta$ is a small, positive parameter (known as the learning rate). 此时， $\Delta C \approx -\eta \| \nabla C \|^2<=0$，这样每次改变 $v$， $C$总是减小的。因此我们的学习规则为：
$v \rightarrow v^{'}=v-\eta \nabla C$

Then we’ll use this update rule again, to make another move. If we keep doing this, over and over, we’ll keep decreasing $C$ until - we hope - we reach a global minimum.

Summing up, the way the gradient descent algorithm works is to repeatedly compute the gradient $\Delta C$, and then to move in theopposite direction, “falling down” the slope of the valley.

关于learning rate $\eta$的选择：(1) $\eta$需要足够小; (2) $\eta$太小会导致学习速度慢。因此需要在两者之间寻找一个平衡。

使用梯度下降法训练神经网络

训练神经网络的目标是找到weights $w_k$ 和biases $b_l$ 使得损失函数 $C$的值最小化。我们可以得到梯度下降的更新规则：
$w_k \rightarrow w_k^{'}=w_k- \eta \frac{\partial C}{\partial w_k}$

$b_l \rightarrow b_l^{'}- \eta \frac{\partial C}{\partial b_l}$

随机梯度下降法(stochastic gradient descent)

标准梯度下降法导致学习太慢的问题：损失函数 $C(w,b)=\frac{1}{2n}\sum_x\|y(x)-a\|^2$可以写作 $C=\frac{1}{n}\sum_xC_x$，其中 $C_x \equiv \frac{\|y(x)-a\|^2}{2}$。
计算梯度 $\nabla C=\frac{1}{n}\sum_x \nabla C_x$时，需要对每个样本都分别计算其梯度，由于训练数据集通常较大，计算会消耗大量的时间。

随机梯度下降可以用来加速学习： 其策略是，通过计算随机选取的一小部分训练样本的 $\nabla C_x$，并计算其平均值来估算整体的梯度 $\nabla C$。
首先随机选取 $m$个训练样本 $X_1, X_2,...,X_m$，视为一个 mini-batch。当 $m$足够大 $m\approx n$时，可以将部分样本梯度的平均值作为 $\nabla C$的估计： $\nabla C \approx \frac{1}{m} \sum_j^m \nabla C_{X_i}$

因此，随机梯度下降的更新规则是：
$w_k \rightarrow w_k^{'}=w_k - \frac{\eta}{m}\sum_j \frac{\partial C_{X_j}}{\partial w_k}$

$b_l \rightarrow b_l^{'} = b_l - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l}$

具体执行过程是：先将数据集随机打乱然后均分成 $k$个mini-batch，对每个mini-batch依次采用上述更新规则，直至遍历完整个数据集（完成k个mini-batch的更新），称之为完成 an epoch of training。然后开始一个新的training epoch。

标准梯度下降与随机梯度下降的比较：
（1）标准梯度下降每次计算完整个数据集的梯度，才进行一次参数更新；随机梯度下降在一轮训练中（遍历完一次数据集）采用多次小批量更新策略，对每个mini-batch都进行一次参数更新。
（2）随机梯度下降的优点：加速学习（不需要等到计算完整个数据集的梯度才进行参数更新）；计算梯度时加入了随机因素，有利于跳出局部极小（机器学习，周志华，P107）。

参考文献：

1. Neural Networks and Deep Learning by Michael A. Nielsen
2. 机器学习，周志华