fireworks-“浪潮杯”第八届山东省ACM省赛C题
onlinejudge:
http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Index/problemdetail/pid/3895.html
Problem Description
Hmz likes to play fireworks, especially when they are put regularly.
Now he puts some fireworks in a line. This time he put a trigger on each firework. With that trigger, each firework will explode and split into two parts per second, which means if a firework is currently in position x, then in next second one part will be in position x−1 and one in x+1. They can continue spliting without limits, as Hmz likes.
Now there are n fireworks on the number axis. Hmz wants to know after T seconds, how many fireworks are there in position w?

Input
Input contains multiple test cases.
For each test case:
The first line contains 3 integers n,T,w(n,T,|w|≤10^5)
In next n lines, each line contains two integers xi and ci, indicating there are ci fireworks in position xi at the beginning(ci,|xi|≤10^5).
Output
For each test case, you should output the answer MOD 1000000007.
Sample Input
1 2 0
2 2
2 2 2
0 3
1 2
Sample Output
2
3
题意
Hmz喜欢放烟花,现在他把烟花放在一排。这一次他在每一支烟花上都扣上了触发器。有了这个触发器,每一个烟花都会爆炸并每秒分裂成两部分,这意味着如果一个烟花当前位于位置X,那么在下一秒,一部分将位于位置X-1,一部分位于X+1。他们可以不受限制地继续分裂,就像Hmz喜欢的那样。
现在数字轴上有n个烟花。嗯,想知道T秒后,W位置有多少烟花?
输入包含多个测试用例。
对于每个测试用例:
第一行包含3个整数n,t,w(n,t,w≤105)
在n行中,每行包含两个整数Xi和Ci,表示在起始位置处有Ci烟花(Ci,Xi=105)。
对于每个测试用例,您应该输出答案mod 10000007。
---------------------------------------------------------------------------------------------------------------------------------------------------------------
以下参考自:https://blog.csdn.net/baidu_36227831/article/details/75948045
我们假设在0的位置有一个烟花
下面这个图给出了在1,2,3,秒时,各个坐标点产生的烟花的数量(蓝色为烟花数量)

仔细观察我们就可以发现这是一个我们很熟悉的数学定理,杨辉三角
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……………………
有了这个之后就很好办了,只要能确定C(n,m)其中的n和m就可以了,不懂得可以参考下面链接,大佬请直接跳过 https://wenku.baidu.com/view/b38a326052d380eb63946d57.html
在这里我们可以看出来n就是题目中给出的T,
要求m需要略作思考,这里我们设一个temp代表所求位置到烟花的绝对值,这里我们以图为例子推演一下,假设所求位置是-1,时间限制是3秒,烟花的初始位置是0,那么两点之间的绝对值temp=1,我们可以发现这里我们要求的m=(T/2)-(temp/2),或者是m=(T+1/2)-(temp+1/2),严格来说第二种是准确的,但是因为这道题目,T和temp只有是同奇同偶的情况下才代表该点有烟花(大家可以对着图演示一下就会发现这个规律),因为同奇同偶导致了两个式子结果是一样的。
上面提到了同奇同偶,但是怎么来确定同奇同偶?我这里是设了两个变量tomd(代表T的奇偶性),temp(所求到烟花的绝对值,这里只需要对temp%2与tmod判等就可以验证是否是同奇同偶)。
这个题用到的主要算法是逆元组合数,用来求组合数的还有lucas,但是而这还有有区别的,逆元求组合数适用于数较小且mod较大时,还要保证mod必须为素数,lucas适用于数较大且mod较小时的组合数
这两个算法这里不展开细讲,要想深入学习,可以看一下其他大牛的讲解
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
上面提到逆元组合数,是为了帮助求比较大的数的取模运算,以下参考自http://www.cnblogs.com/dupengcheng/p/5487362.html
和https://blog.csdn.net/weixin_40149887/article/details/79861045
首先看之前需要了解几个算法:
-
快速幂
百度百科上的解释快速幂就是不同于平时一个数一个数相乘求幂的方法,举个例子,求ab(a的b次方):
a11 = a^( 20 + 21 + 23) = a ^ (20) + a ^ (21) + a ^ (23)
也就是把右上角的次方:11拆成二进制表达方式: 20 + 21 + 23 == 1011
-
快速幂取模算法
这里的快速幂需要知道以下公式:
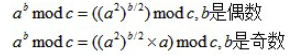
// 依照上面公式,不考虑取模的写法如下:
// a^b
int power_mod(int a, int b) {
int ans = 1;
while (b) {
if (b%2) {
ans *= a;
}
b /= 2;
a *= a;
}
return ans;
}
// 或者用位运算
int power_mod(int a, int b) {
int ans = 1;
while (b) {
if (b & 1) {
ans *= a;
}
b >>= 1;
a *= a;
}
return ans;
}
// 取模版本:
int power_mod(int a, int b, int c) {
int ans = 1;
a %= c;
while (b) {
if (b & 1) {
ans *= a;
ans %= c;
}
b >>= 1;
a *= a;
a %= c;
}
return ans;
}
-
逆元
逆元:对于a和p(a和p互素),若a*b%p≡1,则称b为a%p的逆元。 -
费马小定理
假如a是一个整数,p是一个质数,那么 a^p-a 是p的倍数:
这里写图片描述
如果a不是p的倍数:
这里写图片描述=> a(p-2) * a % p = 1
=> a * a(p-2) % p = 1因此, a(p-2)也是
-
求组合数取模
组合数的求法: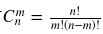
除法的取模和乘法不同,逆元和费马小定理可以帮助求组合数的取模。求(a/b)%p,若已知b%p的逆元是c=> b*c%p = 1,
(a/b)%p = ((ac%p)/(bc%p))%p = (a*c%p)%p = (a%p) (c%p)%p
求解方法:
先算出n!%p、m!%p、(n-m)!%p,用fac[i]表示 i!%p 的值
因为组合数取模是(n!)/(m!(n-m)!)%p,因此需要计算出m!%p、(n-m)!%p的逆元,根据费马小定理,m!%p、(n-m)!%p的逆元分别是(m!)(p-2) 、((n-m)!)(p-2)
快速幂取模求出(m!)(p-2)%p、((n-m)!)(p-2)%p,分别记为M、NM
最后求一下(n!)%p * M * NM % p
还有一篇文章写的也挺好的,在这就不再赘述:http://www.cnblogs.com/dupengcheng/p/5487362.html
有兴趣也可以看一下
下面放出AC代码:
代码
#include <iostream>
#include <algorithm>
#define ll long long
#define inf 0x3f3f3f3f
#define mod 1000000007
using namespace std;
ll dat[100005];
void start() {
dat[0] = 1;
for (ll i = 1; i <= 100000; i++) {
dat[i] = dat[i - 1] * i % mod;
}
}
ll quickpow(ll a, ll b) {
ll base = a, ans = 1;
if (b < 0) return 0;
a %= mod;
while (b) {
if (b % 2) ans = ans * base % mod;
base = base * base % mod;
b /= 2;
}
return ans;
}
ll inv(ll a)
{
return quickpow(a, mod - 2);
}
ll C(ll n, ll m)
{
if (n < m) return 0;
return dat[n] * inv(dat[m]) % mod*inv(dat[n - m]) % mod;
}
int main() {
//freopen("input.txt", "r", stdin);
start();
ll n, t, w;
while (cin >> n >> t >> w) {
ll x, c, sum = 0, tmod = t % 2;
for (ll i = 0; i < n; i++) {
cin >> x >> c;
ll temp = abs(x - w);
if (temp % 2 == tmod && temp <= t) {
sum = (sum + c * C(t, (t - temp) / 2)) % mod;
}
}
cout << sum << '\n';
}
return 0;
}