A - Problem A. Return of the Nim
题型:
博弈
题意:
有n堆石子,两个人进行游戏,每一步有两种操作方式
操作1:从任意堆里拿任意个,
操作2:从所有堆里拿走x个,其中x不小于最小的那堆石子的个数
保证n是质数
题解:
1.威佐夫博弈:有两堆各若干个物品,两个人轮流从任一堆取或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
2.Nim博弈:有N堆物品,每堆有M[i](1 <= i <= N)个物品,两个人轮流从任意一堆上取任意多的物品,最后取光者胜。两人都采取最优策略,问,是先手赢还是后手赢?
3.关于本题,当n=2时,也就是两堆石子的时候,完全符合威佐夫博弈,这一部分可以考虑到。但是当n>2时,这并不是一个严格的尼姆博弈,因为尼姆博弈规定了只能从一堆中选取。这就需要灵活的考虑这个为什么加上操作二也就是从所有堆中取k个仍然是尼姆博弈。这里从网上抄一部分内容。
而进行这个取k个操作会产生什么影响呢,举个例子,(偷挪网上大佬的例子..)
有3堆石子,分别是15,6,9 然后转换为二进制形式
1 1 1 1
0 1 1 0
1 0 0 1
此时为P态,进行普通Nim操作肯定会破会P态转移到N态,所以此时不会选取这种操作,那么只能尝试对每堆进行取任意满足条件的k个石子,发现不管怎么取完之后P态也必定会被破坏。原因是,假如对每堆取K个它们二进制最小的位代表的个数个,则取完之后此位的二进制值都会被取反,所以破坏了P态,而且题目的要求是素数个堆(除2外都是奇数),对其他满足条件的二进制位进行取也是如此。所以当>2堆时,对P态进行取同k个操作只会破坏P态,而不会得到想要的P态——>P态,而当为N态时,只需进行普通的Nim操作就可使N态转化为P态,故加入同取k个操作之后也是满足普通Nim堆的。
代码:
#include<bits/stdc++.h> using namespace std; double _=(sqrt(5)+1)/2.0; double eps=1e-5; int main() { int g,n,a[100],i; cin>>g; while(g--) { cin>>n; for(i=0; i<n; i++) cin>>a[i]; if(n==2) { int a1=min(a[0],a[1]); int a2=max(a[0],a[1]); if(floor((a2-a1)*_)==a1) cout<<"Watson"<<endl; else cout<<"Sherlock"<<endl; } else { int ans=0; for(i=0; i<n; i++) ans^=a[i]; if(ans) cout<<"Sherlock"<<endl; else cout<<"Watson"<<endl; } } return 0; }
B - Problem B. Quadrat
题型:
规律
题意:
求满足以下条件
①.这个数为n位(可以有前导零)
②.取它的平方的后n位,与它本身每一位对应之差≤d(这里的差指的是数字之间的距离,而这个距离是将数字按圈排列,0与9相邻所求得的)
的数字的个数。
题解:
这个题个人觉得数据量不算大, 可以考虑本地打表存入数组(我没看清是否能存下来),当然也可以打表找规律,再写标准代码。(所谓的本地打表就是暴力的情况,直接根据题意来写程序,然后将运行出来的结果存到数组中)
本地打表代码
#include <bits/stdc++.h> using namespace std; typedef long long LL; const int MAX = 10005; const int MOD = 1e9+7; const int INF = 0x3f3f3f3f; int a[15][15]; LL mypow[] = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000}; int main() { memset(a, 0, sizeof(a)); for(int i = 0; i <= 9; ++i) { for(int j = 0; j <= 9; ++j) { a[i][j] = abs(i-j); if(a[i][j] > 5) a[i][j] = 10 - a[i][j]; //cout << a[i][j] << " "; } //puts(""); } for(int n = 1; n <= 7; ++n) { for(int eps = 0; eps <= 3; ++eps) { int tot = 0; for(int i = 0; i < mypow[n]; ++i) { //cout << "i=" << i << endl; int tt = i; LL tm = (i%mypow[n])*(i%mypow[n]); tm %= mypow[n]; int j; for(j = 0; j < n; ++j) { if(a[tm%10][tt%10] > eps) break; tm /= 10; tt /= 10; } if(j == n) { ++tot; // cout << i << endl; } } cout << tot << " "; //cout << "tot=" << tot << endl; } puts(""); } return 0; }
本地打表运行结果:
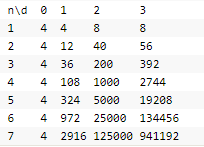
观察发现,对应的【第i行的第j列的值】等于【第i-1行第j列的值】*【(j*2)+1】
代码:
#include <bits/stdc++.h> using namespace std; typedef long long LL; const int MAX = 10005; const int MOD = 1e9+7; const int INF = 0x3f3f3f3f; LL ans[20][5]; void init() { ans[1][0] = ans[1][1] = 4; ans[1][2] = ans[1][3] = 8; for(int n = 2; n <= 18; ++n) for(int d = 0; d <= 3; ++d) ans[n][d] = ans[n-1][d] * (d * 2 + 1); } int main() { init(); int t; int n, d; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&d); printf("%lld\n", ans[n][d]); } return 0; }
C - Problem C. fireworks
题型:
杨辉三角+逆元
题意:
有一种特殊的烟花,他每一秒可以向自己的左右两边分裂相同数量的烟花
求所给位置在T时间后有多少个烟花
要求输入n(烟花的数量),T(烟花的持续时间),w(所求的位置)
接下来n行每一行输入两个数xi(烟花的初始位置) ci(该点的烟花数量)
题解:
我们假设在0的位置有一个烟花
下面这个图给出了在1,2,3,秒时,各个坐标点产生的烟花的数量(蓝色为烟花数量)
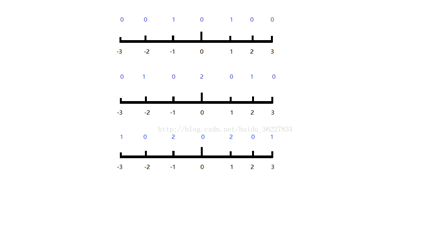
仔细观察我们就可以发现这是一个我们很熟悉的数学定理,杨辉三角
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……………………
杨辉三角的计算过程就是C(n,m)。例如第五行第二个就是C(4,1);
有了这个之后就很好办了,只要能确定C(n,m)其中的n和m就可以了
在这里我们可以看出来n就是题目中给出的T。
要求m需要略作思考,这里我们设一个temp代表所求位置到烟花的绝对值,这里我们以图为例子推演一下,假设所求位置是-1,时间限制是3秒,烟花的初始位置是0,那么两点之间的绝对值temp=1,我们可以发现这里我们要求的m= (T+1/2)-(temp+1/2)。
同时我们看下图,只是将杨辉三角里面填上了0;

这个题用到的主要算法是逆元组合数。
#include <bits/stdc++.h> typedef long long LL; const long long mod = 1e9+7; const int maxn = 1e5+10; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; LL fac[maxn]; void init() { fac[0] = 1; for(int i = 1; i < maxn; i++) { fac[i] = (fac[i-1]*i)%mod; } } LL inv1(LL a) { return a==1?1:(mod-mod/a)*inv1(mod%a)%mod; } LL C(int a,int b) { if(a<b) return 0; return fac[a]*inv1(fac[b]*fac[a-b]%mod)%mod; } int main() { IO; int n,t,w; init(); while(cin>>n>>t>>w) { long long ans=0; for(int i=0; i<n; i++) { int x,c; cin>>x>>c; int l=x-t; int r=x+t; int te=w-l; if(w<l||w>r||te%2!=0) { continue; } else { ans+=(c*C(t,te/2))%mod; ans=ans%mod; } } cout<<ans<<endl; } return 0; }
D - Problem D. HEX
题型:
组合数+逆元+思维
题意:
给你一个类似于蜂巢型的东西,每一次只能向左下,中间和右下走一步,给定你(x,y),问你从(1,1)走到(x,y)这个为位置有多少种情况。
题解:
我们通过观察可以看得出来从(1,1)到(A,B)有两种主要的方式
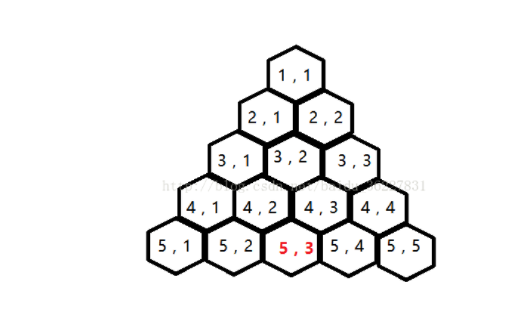
方式一:走的方式中不包括垂直向下
方式二:走的方式中有垂直向下
这里用一个例子来展开
我们假设所求为(1,1)到(5,3)的路径数
我们可以看到,
方式一:需要走两次左下和两次右下。
方式二:①一次左下一次右下,一次垂直向下 ②两次垂直向下
通过比较方式一和方式二我们发现了一件有趣的事,一次垂直向下操作相当于一次左下加一次右下操作
这里我们先来讨论方式一,方式一的路径数是
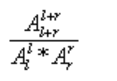
l是左下的次数,r是右下的次数,A代表全排列也就是阶乘
为什么要采用这个公式呢?这个可以看成是一个排列组合的问题,先把所有的步骤全排列然后去掉其中重复的组合数
方式二的求法只要枚举就可以了,枚举方式是,每次left--,right--,down++,这个时候的公式就变成了
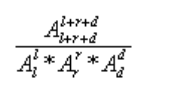
枚举到right或者left其中一个为0,这就代表没有办法再抵消成一个down了
因为本题要求我们mod1e9+7,所以就想到了逆元。
#include <bits/stdc++.h> typedef long long LL; const long long mod = 1e9+7; const int maxn = 2e5+10; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; LL fac[maxn]; LL inv[maxn]; void init() { fac[0] = 1; for(int i = 1; i < maxn; i++) { fac[i] = (fac[i-1]*i)%mod; } } LL inv0(LL a)//递推法求逆元 { return a==1?1:(mod-mod/a)*inv0(mod%a)%mod; } void inv1() { inv[0]=1; for(int i=1;i<maxn;i++) inv[i]=inv0(fac[i]); } int main() { IO; LL a,b; init(); inv1(); while(cin>>a>>b) { LL right=b-1; LL left=a-b; LL down=0; LL sum=0; while(right>=0&&left>=0) { sum=(sum+(((fac[right+left+down]*inv[right])%mod*inv[left])%mod*inv[down])%mod)%mod; right--;left--;down++; } printf("%lld\n",sum); } return 0; }
E - Problem E. news reporter
真~不会
F - Problem F. quadratic equation
题型:
二元一次方程
题意:
用给定的整数a,b,c,要求你判断下面的陈述是否属实:对于任何x,如果a⋅x^2+b⋅x+ c = 0,那么x是一个整数。
题解:
这个题请多次读题,并且需要了解一下离散的内容(可能叫辩证关系?演绎推理?逻辑?)这里有一个说明:如果前件为真,当结论为真时,命题为真,结论为假时,命题为假;如果前件为假,那么命题一定为真,不管结论是否为真。
也就是说只有当前件成立后件不成立时输出 "NO" 其他情况都输出 "YES" 本题就是 当方程有解并且解不为整数时输出 "NO" 其他情况输出 "YES"
代码
#include <bits/stdc++.h> typedef long long LL; const long long mod = 1e9+7; const int maxn = 2e5+10; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; int main() { IO; int T; cin>>T; while(T--) { int a,b,c; cin>>a>>b>>c; if(a==0) { if(b==0&&c==0) cout<<"NO"<<endl; else if(b!=0&&c!=0&&(c%b)!=0) cout<<"NO"<<endl; else cout<<"YES"<<endl; } else if(a!=0) { double temp=(b*b)-(4*a*c); if (temp>=0) { if ((int)sqrt(temp)!=sqrt(temp)) cout<<"NO"<<endl; else { if ((-1*b-(int)sqrt(temp))%(2*a)!=0||(-1*b+(int)sqrt(temp))%(2*a)!=0) cout<<"NO"<<endl; else cout<<"YES"<<endl; } } else cout<<"YES"<<endl; } } return 0; }
G - Problem G. sum of power
题型:
签到 快速幂
题意:
计算从1到n的m次方的和对1E9+7取余。
题解:
简单的快速幂。
代码:
#include <bits/stdc++.h> typedef long long LL; const long long mod = 1e9+7; const int maxn = 2e5+10; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; LL poww(LL a, LL b, LL c)//a^b%c { LL ans = 1; a = a % c; while(b>0) { if(b % 2 == 1) ans = (ans * a) % c; b = b/2; a = (a * a) % c; } return ans; } int main() { IO; int m,n; while(cin>>n>>m) { LL ans=0; for(int i=1; i<=n; i++) ans=(ans+poww(i,m,mod))%mod; cout<<ans<<endl; } return 0; }
H - Problem H. triangle
真~不会
I - Problem I. Parity check
题型:
签到 规律
题意:
给出 f(n) 的递推式以及 n 的值,求 f(n)%2 的结果。
题解:
简单的找规律。给定的数会很大,一定要用数组存储。对2取余实际就是求奇偶。找出规律是一个偶数后接着两个奇数。所以对3取余,如果余数是0(代表偶数)输出0,余数是1(代表奇数)或者2则输出1。
代码:
#include <bits/stdc++.h> typedef long long LL; const long long mod = 1e9+7; const int maxn = 2e5+10; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; int main() { IO; char a[1010]; while(cin>>a) { int len=strlen(a); int sum=0; for(int i=0;i<len;i++) { sum=(sum*10+a[i]-48)%3;//记得每次都要对3取余 } if(sum%3==0) cout<<0<<endl; else cout<<1<<endl; } return 0; }
J - Problem J. company
题型:
贪心
题意:
商店买东西,有n种商品,每种商品卖出去以后得到的价值是v,每种商品有c件,第i天卖出v价值的商品,得到的价值是i*v,时间是从第一天开始,每天只能卖一件,对于每件商品你可以选择卖或者不卖,求卖了这些商品的最大利益是多少。
题解:
把这个题归类到贪心里面去吧,最后求最大利益。中间需要对商品的价格进行排序。
把所有商品的价值存在数组中(包括数量大于一的),排序并顺便求出当前的 ans 。
然后从数组最左边开始枚举,判断是否需要去除当前商品,若去除,则 ans-=a[i]-sum[top-1]+sum[i] ,因为总天数减少了一天,所以后面的所有商品价值和也应该减少。
判断如果当前得到新的 ans 变小了,跳出,输出最大的 ans 。
代码:
#include <bits/stdc++.h> typedef long long LL; const long long INF = 0x3f3f3f3f; const long long mod = 1e9+7; const int maxn = 100000; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; int a[maxn],sum[maxn],d[maxn]; int main() { IO; int n; while(cin>>n) { int logo=n; for(int i=0; i<n; i++) cin>>a[i]; for(int i=0; i<n; i++) { cin>>d[i]; for(int j=1; j<d[i]; j++) a[logo++]=a[i]; } sort(a,a+logo); sum[0]=a[0]; LL ans=a[0]; for(int i=1; i<logo; i++) { sum[i]=sum[i-1]+a[i]; ans+=(i+1)*a[i]; } for(int i=0; i<logo; i++) { LL s=ans-a[i]-sum[logo-1]+sum[i]; if(s>ans) ans=s; else break; } cout<<ans<<endl; } return 0; }
K - Problem K. CF
题型:
贪心+背包
题意:
在持续t分钟的比赛中有n个问题,对于第i个问题,你可以得到ai-di * ti的分数,其中ai表示初始分数,di表示每分钟下降的分数(从比赛开始计数),ti代表解决问题时的分钟数(从比赛开始算起)。现在你知道艾德可以在多长解决第一个问题。你能帮他尽可能多的得分吗?
题解:
直接贪心肯定是不行的。
假设我们此时贪心出来一个做题顺序,使得减少的分数按照相对时间来讲最小。
那么我们直接按序模拟是不行的。因为涉及到这样一点:当前题目做不做对后边是有影响的。一道题的分数高不高和做题时间都会对后边内容有所影响的。
所以我们现在如果有一个相对贪心的顺序之后,我们不妨看做时间为花费,得到的收益就是a【i】.val-a【i】.del*tottime.
那么这里做一个01背包就行。那么考虑如何排序:
我们不能根据减小的速度来评判一个题是否有序,因为这一道题的时间也会影响下一个题的减少量。所以我们排序应当按照单位时间来排序。
那么总结概述就是:按照题的单位时间减少分数从小到大排序,然后做一个01背包即可。
代码:
#include <bits/stdc++.h> typedef long long LL; const long long INF = 0x3f3f3f3f; const long long mod = 1e9+7; #define IO ios::sync_with_stdio(false);\ cin.tie(0);\ cout.tie(0); using namespace std; struct node { int val; int del; int tim; } a[5500]; int dp[70000]; int cmp(node a,node b) { return (double)a.del/(double)a.tim>(double)b.del/(double)b.tim; } int main() { int n,m; while(cin>>n>>m) { memset(dp,0,sizeof(dp)); for(int i=0; i<n; i++) cin>>a[i].val; for(int i=0; i<n; i++) cin>>a[i].del; for(int i=0; i<n; i++) cin>>a[i].tim; sort(a,a+n,cmp); for(int i=0; i<n; i++) { for(int j=m; j>=a[i].tim; j--) { dp[j]=max(dp[j],dp[j-a[i].tim]+a[i].val-a[i].del*j); } } int ans=0; for(int i=0; i<=m; i++) ans=max(ans,dp[i]); cout<<ans<<endl; } return 0; }