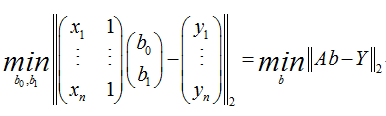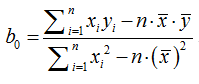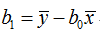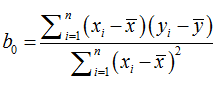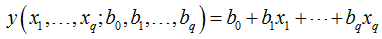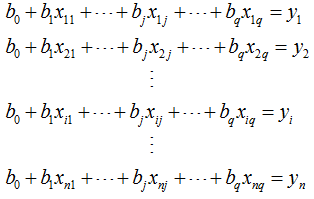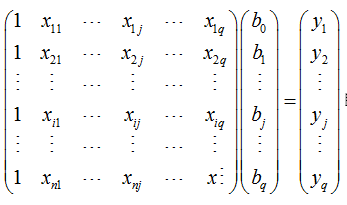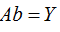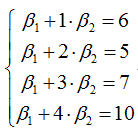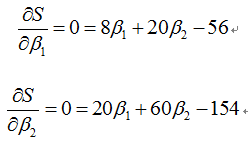转载自: https://blog.csdn.net/zengxiantao1994/article/details/70210662
文章仅为创作者的观点,可与转载者讨论
最小二乘法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
线性函数模型
典型的一类函数模型是线性函数模型。最简单的线性式是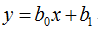
直接给出该式的参数解:
其中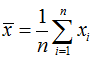
一般线性情况
若含有更多不相关模型变量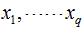
即线性方程组:
通常人们将xij记作数据矩阵 A,参数bj记做参数向量b,观测值yi记作Y,则线性方程组又可写成:
上述方程运用最小二乘法导出为线性平方差计算的形式为: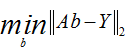
最后的最优解为: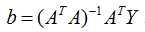
示例
实验得到4个数据(x, y):(1, 6)、(2, 5)、(3, 7)、(4, 10)。希望找出一条和这四个点最匹配的直线: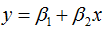
最小二乘法采用的手段是尽量使得等号两边的方差最小:
求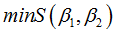
得到β1=3.5,β2=1.4。所以: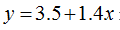
MATLAB实现
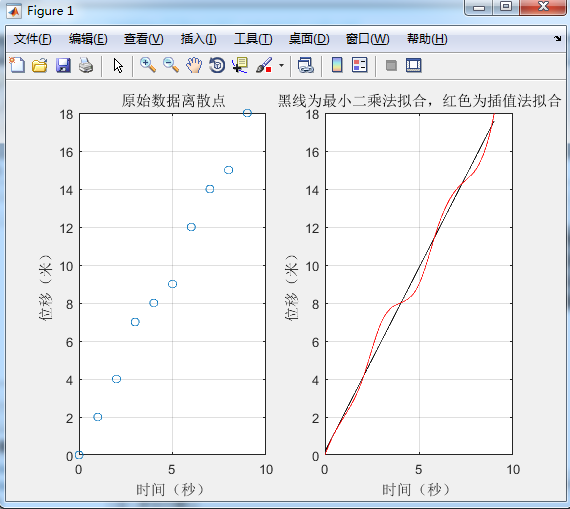
例一:小车时间与位移关系
% 小车时间(xi)和位移关系(yi)关系
x = [0 1 2 3 4 5 6 7 8 9];
y = [0 2 4 7 8 9 12 14 15 18];
%{
subplot(m,n,p) 其中前两个参数 m,n是指将你的图分成 m*n个栅格,
每个栅格用 p 来编号,而编号是按行(横着)编号的,所以,当 m = 2,n = 2时编号规则为
<span class="hljs-number">1</span> | <span class="hljs-number">2</span>
------
<span class="hljs-number">3</span> | <span class="hljs-number">4</span>
所以subplot(<span class="hljs-number">2</span>,<span class="hljs-number">2</span>,[<span class="hljs-number">1</span> <span class="hljs-number">3</span>]),就说明你这一个子图占据的是 <span class="hljs-number">1</span>, <span class="hljs-number">3</span>两个栅格,
而subplot(<span class="hljs-number">2</span>,<span class="hljs-number">2</span>,<span class="hljs-number">2</span>)说明子图仅占据第<span class="hljs-number">2</span>个栅格.
%}
subplot(1,2,1);
plot(x,y,‘o’);
% 图形的一些设置
xlabel(‘时间(秒)’);
ylabel(‘位移(米)’);
title(‘原始数据离散点’)
%{
grid on:是打开网格
grid off:是关闭网格
而grid是切换两种状态,如果在grid off的状态下,输入grid,相当于grid on
相反,如果在grid on状态下输入grid 等价于grid off
%}
grid on
%{
polyfit函数是matlab中用于进行曲线拟合的一个函数。其数学基础是最小二乘法曲线拟合原理。
曲线拟合:已知离散点上的数据集,即已知在点集上的函数值,构造一个解析函数(其图形为一曲线)使在原离散点上尽可能接近给定的值。
调用方法:polyfit(x,y,n)。用多项式求过已知点的表达式,
其中x为源数据点对应的横坐标,可为行向量、矩阵;
y为源数据点对应的纵坐标,可为行向量、矩阵;
n为你要拟合的阶数,一阶直线拟合,二阶抛物线拟合,并非阶次越高越好,看拟合情况而定。
多项式在x处的值y可用下面程序计算:y=polyval(a,x,m)
%}
p = polyfit(x,y,1)
% 0:0.01:9 起始为0,终点为9,步长0.01
x1 = 0:0.01:9;
y1 = polyval(p,x1);
x2 = 0:0.01:9;
%{
MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,‘method’)
其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量,
'method’表示采用的插值方法,MATLAB提供的插值方法有几种:
'nearest’是最邻近插值, 'linear’线性插值; 'spline’三次样条插值; 'pchip’立方插值.缺省时表示线性插值
注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
%}
y2 = interp1(x,y,x2,‘spline’);
subplot(1,2,2);
plot(x1,y1,‘k’,x2,y2,‘r’)
xlabel(‘时间(秒)’);
ylabel(‘位移(米)’);
title(‘黑线为最小二乘法拟合,红色为插值法拟合’)
grid on
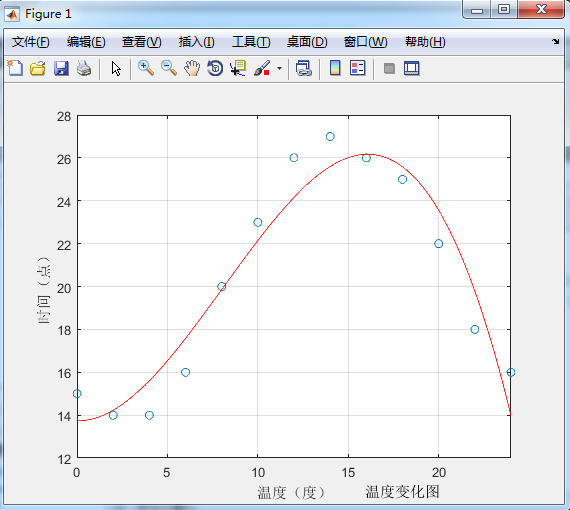
例二:温度和时间关系
%{
例如:对某日隔两小时测一次气温。设时间为ti,气温为Ci,i = 0,2 ,4,…,24。数据如下:
表<span class="hljs-number">2</span> 温度(Ci)随时间(ti)变化关系
-----------------------------------------------------------
ti <span class="hljs-number">0</span> <span class="hljs-number">2</span> <span class="hljs-number">4</span> <span class="hljs-number">6</span> <span class="hljs-number">8</span> <span class="hljs-number">10</span> <span class="hljs-number">12</span> <span class="hljs-number">14</span> <span class="hljs-number">16</span> <span class="hljs-number">18</span> <span class="hljs-number">20</span> <span class="hljs-number">22</span> <span class="hljs-number">24</span>
-----------------------------------------------------------
ci <span class="hljs-number">15</span> <span class="hljs-number">14</span> <span class="hljs-number">14</span> <span class="hljs-number">16</span> <span class="hljs-number">20</span> <span class="hljs-number">23</span> <span class="hljs-number">28</span> <span class="hljs-number">27</span> <span class="hljs-number">26</span> <span class="hljs-number">25</span> <span class="hljs-number">22</span> <span class="hljs-number">18</span> <span class="hljs-number">16</span>
-----------------------------------------------------------
%}
x = [0 2 4 6 8 10 12 14 16 18 20 22 24]
y = [15 14 14 16 20 23 26 27 26 25 22 18 16]
plot(x,y,‘o’)
grid on
%{
hold on 和hold off,是相对使用的
前者的意思是,你在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到
后者表达的是,你在当前图的轴(坐标系)中画了一幅图,此时,状态是hold off,则再画另一幅图时,
原来的图就看不到了,在轴上绘制的是新图,原图被替换了
%}
hold on
% 三阶拟合 得到的 p = -0.0061 0.1474 -0.0246 13.7390是个多项式的系数
% 即拟合的曲线y = -0.0061*x3 + 0.1474*x2 - 0.0246*x + 13.7390 (其中x3表示x的3次方,x2同理)
p = polyfit(x,y,3)
x1 = 0:0.01:24
y1 = polyval(p,x1)
plot(x1,y1,‘r’)
% axis坐标轴范围设置
axis([0 24 12 28])
xlabel(‘温度(度)’);
ylabel(‘时间(点)’);
title(‘温度变化图’,‘position’, [18,10])