高斯过程（Gaussian Processes）原理

高斯过程（Gaussian Processes, GP）是概率论和数理统计中随机过程的一种，是多元高斯分布的扩展，被应用于机器学习、信号处理等领域。博主在阅读了数篇文章和博客后才算是基本搞懂了GP的原理，特此记录。本文目前暂对高斯过程的公式推导和高斯过程回归原理及其优缺点进行讲解和阐述，后续根据个人学习进度再更新源码等内容。

一、一维高斯分布

我们从最简单最常见的一维高斯分布开始。

众所周知，一维高斯分布，又叫一维正态分布的概率密度函数为：

$p\left ( x \right )=\frac{1}{\sigma \sqrt{2\pi }}exp\left ( \frac{-\left ( x-\mu \right)^{2}}{2\sigma ^{2}} \right ) \left ( 1\right )$

式中， $\mu$ 表示均值， $\sigma$ 表示方差，均值和方差唯一的决定了曲线的形状。当 $\mu$ 为0， $\sigma$ 为1时称为标准正态分布。

二、多维高斯分布

从一维高斯分布推广到多维高斯分布。

假设各维度之间相互独立，则其概率密度函数为：

$p\left ( x _{1}, x _{2}, ..., x _{n}\right )=\prod_{i=1}^{n}p\left ( x_{i} \right )=\frac{1}{\left ( 2\pi \right )^{\frac{n}{2}}\sigma _{1}\sigma _{2}...\sigma _{n}}exp\left ( -\frac{1}{2}\left [ {\frac{(x_{1}-\mu _{1})^{2}}{\sigma _{1}^{2}}}+{\frac{(x_{2}-\mu _{2})^{2}}{\sigma _{2}^{2}}}+...+{\frac{(x_{n}-\mu _{n})^{2}}{\sigma _{n}^{2}}} \right ] \right)\left ( 2 \right )$

其中， $\mu _{1}, \mu _{2},...$ 分别是第一维、第二维...的均值， $\sigma _{1}, \sigma _{2}, ...$ 分别是第一维、第二维...的方差。

使用向量和矩阵表示上式，令

$\vec{x}-\vec{\mu }=\left [ x_{1}-\mu _{1}, x_{2}-\mu _{2}, \cdots , x_{n}-\mu _{n} \right ]^{T}\left ( 3 \right )$

$K =\begin{bmatrix} \sigma _{1}^{2}& 0& \cdots & 0\\ 0& \sigma _{2}^{2}& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \cdots & \sigma _{n}^{2} \end{bmatrix}\left ( 4 \right )$

则有

$\sigma _{1}\sigma _{2}\cdots \sigma _{n}=\left | K \right |^{\frac{1}{2}}\left ( 5 \right )$

${\frac{(x_{1}-\mu _{1})^{2}}{\sigma _{1}^{2}}}+{\frac{(x_{2}-\mu _{2})^{2}}{\sigma _{2}^{2}}}+\cdots +{\frac{(x_{n}-\mu _{n})^{2}}{\sigma _{n}^{2}}}=\left (\vec{x}-\vec{\mu} \right )^{T}K^{-1}\left (\vec{x}-\vec{\mu} \right )\left ( 6 \right )$

将公式（5）和公式（6）代入公式（2）可得

$p\left ( \vec{x} \right )=\left ( 2\pi \right )^{-\frac{n}{2}}\left | K \right |^{-\frac{1}{2}}exp\left ( -\frac{1}{2}\left ( \vec{x}- \vec{\mu }\right )^{T}K^{-1}\left ( \vec{x}- \vec{\mu }\right ) \right ) \left ( 7 \right )$

其中， $\vec{\mu }\in \mathbb{R}^{n}$ 是均值向量， $K\in \mathbb{R}^{n\times n}$ 是协方差矩阵，由于我们假设了各维度之间是相互独立的，所以 $K$ 是一个对角矩阵。当各维度变量相关时，上式的形式仍然一致，但此时协方差矩阵不再是对角矩阵，只具备半正定和对称的性质。上式通常也简写为：

$x\sim N\left (\vec{ \mu }, K \right ) \left ( 8 \right )$

三、高斯过程

在概率论和统计学中，高斯过程(Gaussian process, GP)是观测值出现在一个连续域(例如时间和空间)的随机过程。在高斯过程中，连续输入空间中每一点都是与一个正态分布的随机变量相关联。此外，这些随机变量的每个有限集合都有一个多维正态分布，换句话说他们的任意有限线性组合是一个正态分布。高斯过程的分布是所有(无限多个)随机变量的联合分布，正因如此，它是连续域(例如时间和空间)上的函数分布。

下面通过一个例子来了解一下高斯过程。

假设我们在周一到周四每天的 7:00 测试了 4 次心率，如下图中 4 个点，可能的高斯分布如图所示（瘦高的那条）。这是一个一维高斯分布，只有每天 7: 00 的心率这个维度。

现在不仅在每天的 7: 00 测心率（横轴），在 8:00 时也进行测量（纵轴），这个时候变成两个维度（二维高斯分布），如下图所示。

更进一步，如果我们在每天的无数个时间点都进行测量，则变成了下图的情况。注意下图中把测量时间作为横轴，则每个颜色的一条线代表一个（无限个时间点的测量）无限维的采样。当对每次对无限维进行采样得到无限多个点时，其实可以理解为我们采样得到了一个函数。

当从函数的视角去看待采样，理解了每次采样无限维相当于采样一个函数之后，原本的概率密度函数就不再是点的分布，而变成了函数的分布。这个连续的无限维高斯分布就是高斯过程。用偏理论的话语表述就是，对于所有 $\vec{x}=\left [ x_{1}, x_{2}, \cdots , x_{n}\right ]$ ， $f\left ( \vec{x} \right )=[f\left ( x_{1} \right ), f\left ( x_{2} \right ),\cdots , f\left ( x_{n} \right )]$ 都服从多元高斯分布，则称 $f$ 是一个高斯过程，表示为：

$f\left (\vec{ x} \right )\sim N\left ( \mu \left ( x \right ), K\left ( x,x \right ) \right ) (9)$

一个高斯过程被一个均值函数和协方差函数唯一地定义，并且一个高斯过程的有限维度的子集都服从一个多元高斯分布（为了方便理解，可以想象二元高斯分布两个维度各自都服从一个高斯分布）。

同时，高斯过程的协方差函数就是其核函数。核函数是高斯过程的核心，它决定了一个高斯过程的性质。核函数在高斯过程中起衡量任意两个点之间的“距离”的作用。不同的核函数有不同的衡量方法，得到的高斯过程的性质也不一样。最常用的一个核函数为高斯核函数，也就是径向基函数 RBF。其基本形式如下，其中 $\sigma$ 和 $l$ 是高斯核的超参数。

$K\left ( x_{i}, x_{j} \right )=\sigma ^{2}exp\left ( -\frac{\left \| x_{i}-x_{j} \right \|_{2}^{2}}{2l^{2}} \right )$

$x_{i}$ 和 $x_{j}$ 表示高斯过程连续域上的两个不同的时间点， $\left \| x_{i}-x_{j} \right \|^{2}$ 是一个二范式，简单点说就是表示 $x_{i}$ 和 $x_{j}$ 之间的距离。

一些常用的核函数如下：

四、高斯过程回归

高斯过程回归是使用高斯过程先验对数据进行回归分析的非参数模型（指系统的数学模型中非显式地包含可估参数）。简单来讲可以看作是根据先验+观测值推出后验的过程。

根据均值 $\mu \left ( x \right )$ 和协方差 $K\left ( x_{i}, x_{j} \right )$ ，我们可以定义一个高斯过程，但是此时并没有任何的观测值，是一个先验。在获得了一组观测值之后，可以根据观测值修正这个高斯过程的均值函数和核函数。

设 $S$ 为训练集，训练数据独立同分布，分布未知，我们定义高斯过程回归模型(Gaussian Process Regression，以下简称GPR)的表达式为：

其中 $\varepsilon _{i}$ 是独立同分布的噪声变量，服从 $N\left ( 0, \sigma ^{2} \right )$ 。

在GPR中，我们假设 $f$ 服从均值为0的GP：

设 $T$ 是测试集，独立同分布且和 $S$ 的分布相同。

定义：

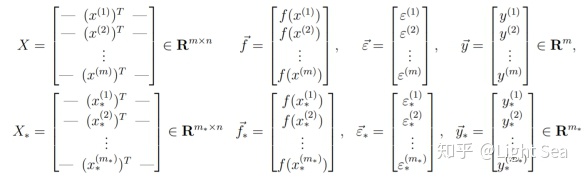
我们的任务就是计算posterior predictive distribution $P\left ( y^{*}|x^{*}, S \right )$ ，既然 $f$ 满足GP，噪声 $\varepsilon$ 也满足高斯分布，根据高斯分布性质可知，这个分布一定是高斯分布。

根据高斯过程的性质，有:

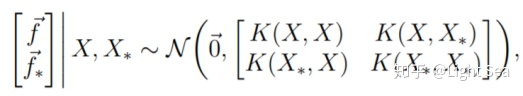
其中：

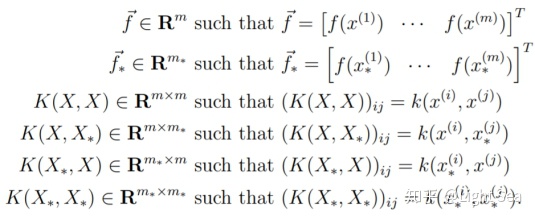
同样的，对噪声也有类似的结论：

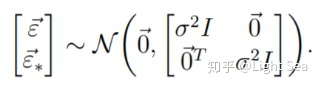
因为两个独立多元高斯变量的和还是多元高斯变量，因此有：

根据多元高斯分布的性质(性质3)，可以看出， $y^{*}$ 满足多元高斯分布：

利用这个性质有：

上式的具体推导可以参考此链接。

这样就完成了预测。

五、高斯过程回归算法的优缺点

优点
- （采用 RBF 作为协方差函数）具有平滑性质，能够拟合非线性数据；
- 高斯过程回归天然支持得到模型关于预测的不确定性（置信区间），直接输出关于预测点值的概率分布；
- 通过最大化边缘似然这一简洁的方式，高斯过程回归可以在不需要交叉验证的情况下给出比较好的正则化效果。
缺点
- 高斯过程是一个非参数模型，每次的 inference 都需要对所有的数据点进行（矩阵求逆）。对于没有经过任何优化的高斯过程回归，n个样本点时间复杂度大概是 $O\left ( n^{3} \right )$ ，空间复杂度是 $O\left ( n^{2} \right )$ ，在数据量大的时候高斯过程变得 intractable；
- 高斯过程回归中，先验是一个高斯过程，likelihood 也是高斯的，因此得到的后验仍是高斯过程。在 likelihood 不服从高斯分布的问题中（如分类），需要对得到的后验进行 approximate 使其仍为高斯过程；
- RBF 是最常用的协方差函数，但在实际中通常需要根据问题和数据的性质选择恰当的协方差函数。

六、参考链接

高斯过程 Gaussian Processes 原理、可视化及代码实现 -

高斯过程回归 - 简书

如何通俗易懂地介绍 Gaussian Process？ - 知乎

[公式推导]用最简洁的方法证明多元正态分布的条件分布 - 司徒鲜生 - 博客园

高斯过程和高斯过程回归 - 知乎