最短路径之迪杰斯特拉算法（Dijkstra）——贪心算法

迪杰斯特拉（Dijkstra)算法主要是针对没有负值的有向图，求解其中的单一起点到其他顶点的最短路径算法。本文主要总结迪杰斯特拉（Dijkstra）算法的原理和算法流程，最后通过程序实现在一个带权值的有向图中，选定某一个起点，求解到达其它节点的最短路径。

1.算法原理

迪杰斯特拉（Dijkstra）算法是一个按照路径长度递增的次序产生最短路径的算法。主要特点是以起始点为中心按照长度递增往外层层扩展（广度优先搜索的思想），直到扩展到终点为止。

选择最短路径顶点的时候依照的是实现定义好的贪心准则，所以该算法也是贪心算法的一种。
首先，我们引进一个辅助数组Distance，它的每个分量D[i]表示当前所找到的从起始点v0到每个终点vi的最短路径长度。

它的初态为：若 $v_{0}$ 到 $v_{i}$ 有弧，则 $D[i]$ 为弧上的权值；
否则，置 $D[i]$ 为 $∞$ 。
显然，此时长度为
$D[j]=Min\{D[i]|v_{i}∈V\}$
的路径就是从 $v_{0}$ 出发长度最短（为1）的一条路径，此时路径为 $(v_{0},v_{i})$ 。
那么下一条长度次短的最短路径是哪一条？
假设该次短路径的终点是 $v_{k}$ ，则这条路径要么是 $(v_{0},v_{k})$ ，要么是 $(v_{0},v_{j},v_{k})$ ，即两者最短的那一条。
其中， $v_{j}∈S$ ，S为当前已求得最短路径的终点的集合；V为待求解的最短路径的顶点集合。

问题一：
为什么下一条次短路径要这样选择？（贪心准则的正确性）
不失一般性，假设S为已经求得最短路径的顶点集合，下一条最短路径的终点是 $x$ ，利用反证法，若此路径有一条顶点不在 $S$ 中，则说明存在一条终点不在S而长度比此路径长度短的路径，但是这显然是矛盾的，因为我们是按照路径长度递增的次序来产生最短路径的。
所以，下一条长度次短的路径长度应该是：
$D[j] = Min\{D[i] | v_{i}∈V-S\}$
其中, $D_{i}$ 或者是弧 $(v_{0},v_{i})$ 上的权值，或者是 $D[k](v_{k}∈S)$ 和弧 $(v_{k},v_{i})$ 上的权值之和。

问题二：
这样产生的路径是否就是S中对应顶点的最短路径？

假设以当前长度来看，假设当前长度对应的顶点v，若长度再增加，是不可能产生权值更短的路径的(对于v来说)，因为长度增加的路径肯定包含此时长度的子路径，而此时选择的路径是该长度下最短的路径；
以一个顶点来看，源点 $v_{0}$ 到一顶点 $v_{k}$ 的最短路径的子路径 $v_{0}$ 到 $v_{i}$ 肯定也是该长度对应的最短路径（即 $v_{0}$ 到 $v_{i}$ 的最短路径），所以这也是我们为什么在S中选择中转结点的原因。
其中很大一部分原因是最短路径的最优子结构，即全局的最优解（ $v_{0}到v_{k}$ ）包含局部的最优解( $v_{0}$ 到v_{i})，且全局的最优解能够通过局部最优解逐步构造。

这也是迪杰斯特拉算法的贪心策略能取得最优解的原因。

2.算法流程

根据上面的算法思想，我们有下面算法的实现流程：
假设用带权值的邻接矩阵arcs来表示带权的有向图，arcs[i][j]表示弧 $<v_{i},v_{j}>$ 上的权值。若 $<v_{i},v_{j}>$ 不存在，则置arcs[i][j]为 $∞$ （计算机上允许的最大值）

1)初始化：已求顶点集S，初始状态为空集；从 $v_{0}$ 出发到图上其余各顶点（终点） $v_{i}$ 可能到达的最短路径长度初值：
$Distance[i] = arcs[locate(G,v_{0})][i] \ v_{i}∈V$
2)选择结点 $v_{j}$ ，使得
$Distance[j] = Min\{Distance[i] \ | \ v_{i}∈V -S \}$
$v_{j}$ 就是当前求的从 $v_{0}$ 出发的最短路径的终点。令
$S = S \cup {j}$
3)修改从 $v_{0}$ 出发到集合 $V-S$ 上的任一顶点 $v_{k}$ 可达的最短路径长度。
若 $Ditance[j] + arcs[j][k] < Distance[k]$
则修改 $Distance[k] = Ditance[j] + arcs[j][k]$
4)重复(2)(3)共 $n-1$ 次，求的 $v_{0}$ 到其余个顶点的最短路径是依路径长度递增的序列。

其中，最短路径的存储可以采用一个path数组，存储到某结点的最短路径中该结点的前驱结点在图中的位置（起点 $v_{0}$ 的前驱可以设成 $-1$ ）。

即若有下面这样一个带全有向图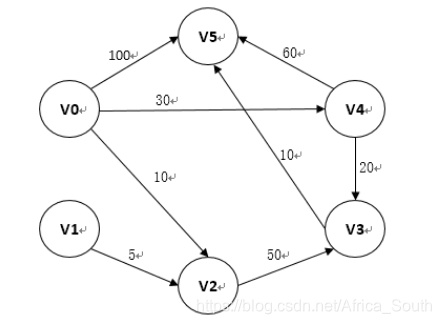：有向网举例
其邻接矩阵如下：
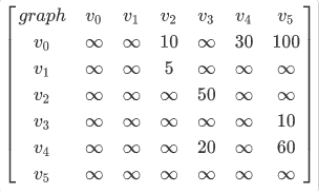
网的邻接矩阵
则迪杰斯特拉算法求解过程：
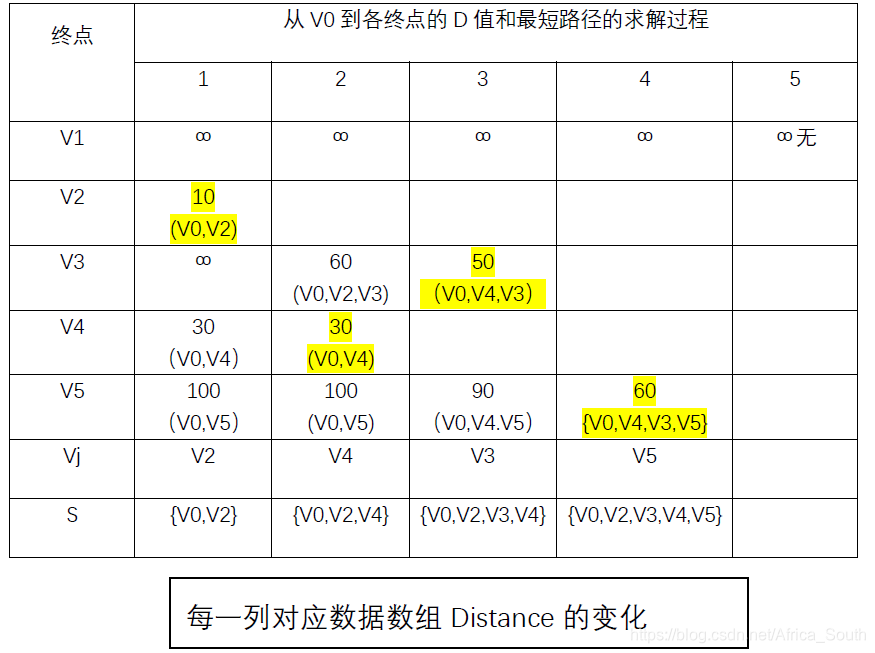
迪杰斯特拉示例

3.算法实现

迪杰斯特拉算法：

void ShortestPath_DIJ(MGraph G, int v0, int* path, int* distance) {
	/*用Dijkstra算法求v0到其余顶点的最短路径p[n]和带权长度distance[n]
	final[i]=1表示已求得v0到vi的最短路径
	*/
	int* final = new int[G.vexnum]; 
	int i;
	distance[v0] = 0; // 初始化
	path[v0] = -1; // 指示当前结点在最短路径中的前驱结点号
	final[v0] = 1;
	for (i = 0; i < G.vexnum; i++) {
		if (i == v0) continue;
		distance[i] = G.arcs[v0][i];
		if(distance[i] != INT_MAX)
			path[i] = v0;
		else path[i] = -1;
		final[i] = 0; 
	}
	for (i = 1; i < G.vexnum; i++) { // 寻找到其余G.vexnum-1个结点的路径
		int min = INT_MAX; // 当前所知里v0顶点的最短距离
		int index = 0;     // 最短距离对应的下标
		int j;
		for (j = 0; j < G.vexnum; j++) {
			if (!final[j]) {    // j在V-S中
				if (distance[j] < min) {
					min = distance[j];
					index = j;
				}
			}
		}// 寻找最短路径
		final[index] = 1;  // 离v0最近的顶点Index并入S
		for (j = 0; j < G.vexnum; j++) { // 更新距离矩阵，一定要判断是否达，即arcs[][]!=OO，否则会整数溢出
			if (!final[j] && G.arcs[index][j] != INT_MAX && (min + G.arcs[index][j] < distance[j])) {
				distance[j] = min + G.arcs[index][j];
				path[j] = index;
			}
		}
	}
	delete[] final;
}

完整测试用例

#include <iostream>
#include <string>
#include <stack>

using namespace std;

#define MAX_VEX_NUM 50
// 定义图的邻接矩阵存储
typedef struct MGraph {
	int arcs[MAX_VEX_NUM][MAX_VEX_NUM];
	string vexs[MAX_VEX_NUM];
	int arcnum, vexnum;
}MGraph;
void createGraph(MGraph& G);
int locate(MGraph G, string u);
void ShortestPath_DIJ(MGraph G,int v0,int* path,int* distance);
void showMatrix(MGraph G);
void showpath(MGraph G,int* path, string u); // 打印从v0到u的路径
int main() {
	MGraph G;
	createGraph(G);
	showMatrix(G);
	int* path = new int[G.vexnum];
	int* distance = new int[G.vexnum];
	ShortestPath_DIJ(G, 0,path,distance);
	cout << "最后的路径数组:\n";
	cout << "V0--V1:"; showpath(G, path, "V1");
	cout << "V0--V2:"; showpath(G, path, "V2");
	cout << "V0--V3:"; showpath(G, path, "V3");
	cout << "V0--V4:"; showpath(G, path, "V4");
	cout << "V0--V5:"; showpath(G, path, "V5");

	system("pause");
	return 0;
}
void showpath(MGraph G,int* path, string u) {
	stack<int> stk;
	int v = locate(G, u);
	stk.push(v);
	int parent = path[v];
	if (parent == -1) cout << "V0到" << u << "没有路径";
	while (parent != -1) {
		stk.push(parent);
		parent = path[parent];
	}
	while (!stk.empty()) {
		int index = stk.top(); stk.pop();
		cout << G.vexs[index];
		if (!stk.empty()) cout << "-->";
	}
	cout << endl;
}
void showMatrix(MGraph G) {
	cout << "图的邻接矩阵:\n";
	for (int i = 0; i < G.vexnum; i++) {
		for (int j = 0; j < G.vexnum; j++) {
			if (G.arcs[i][j] == INT_MAX)
				cout << "oo" << " ";
			else 
				cout << G.arcs[i][j] << " ";
		}
		cout << endl;
	}
}
void createGraph(MGraph& G) {
	cout << "输入图的顶点数和边数:\n";
	cin >> G.vexnum >> G.arcnum;
	cout << "输入图的顶点信息:\n";
	int i;
	for (i = 0; i < G.vexnum; i++) cin >> G.vexs[i];
	// 初始化邻接矩阵
	int j;
	for (i = 0; i < G.vexnum; i++) {
		for (j = 0; j < G.vexnum; j++)
			G.arcs[i][j] = INT_MAX;
	}
	cout << "输入图的边的权值信息vi vj weight:\n";
	for (i = 0; i < G.arcnum; i++) {
		string v1, v2;
		int weight;
		cin >> v1 >> v2 >> weight;
		int l1 = locate(G, v1);
		int l2 = locate(G, v2);
		G.arcs[l1][l2] = weight;
	}
}
int locate(MGraph G, string u) {
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != u; i++);
	if (i == G.vexnum) return -1;
	else return i;
}

这里我用的是栈倒序输出，当然也有其它存储最短路径的方法。

测试用例（即上面的有向网）:

6 8
V0 V1 V2 V3 V4 V5
V0 V5 100
V0 V4 30
V0 V2 10
V1 V2 5
V2 V3 50
V3 V5 10
V4 V5 60
V4 V3 20

4.时间复杂度

两个FOR循环嵌套，最后的时间复杂度为 $O(n^{2})$ 。
若想要求源点到某一顶点的最短路径，也可以用Dijkstra算法，复杂度一样；
但是若要求每一对顶点间的最短路径，可以调用Dijkstra算法n次，复杂度 $O(n^{3})$ ，也可以用弗洛伊德算法（Floyd)，复杂度也是 $O(n^{3})$ ，但是形式上看起来简单一点。

参考资料

《数据结构c语言版》严蔚敏著