引言
SVM的数学推导真的是我一生的痛,看看觉得很懂,但是过了3秒,就在纠结,为什么可以这样换算?今天早上在看集成学习的时候,讲课的老师一直说SVM、SVM、SVM。。。嗯,没错,我又开始回想SVM的数学推导过程,然后,我的一个早上就这样没了。
这次趁着刚看完印象深刻,我想将刚厘清的思路写下来。仅包括如何推出最优化问题,后面的推导我打算等看完凸优化课程再记录,推导过程参考林轩田老师教授的《机器学习技法》内容。
回顾线性分类
线性分类的分类器表达式为\[ \begin{equation} h(x) = sgn(w^Tx + b) \end{equation} \]
林老师之前讲线性分类时用的是PLA算法,即根据当前分类器是否将所有的点分类正确\((h(x)==y)\)。如果有一个点分类错误,那么朝着这个点或偏离这个点更新。算法一直迭代直到所有的点正确分类为止。PLA算法得到的分类器不唯一,仅凭线的初始位置这一个因素便能影响最终的分类器。
但是我们知道最想要的分类器长什么样子。我们希望这个分类器足够"胖",也就是说,这根线变胖的时候,边上的点越迟碰到它越好。
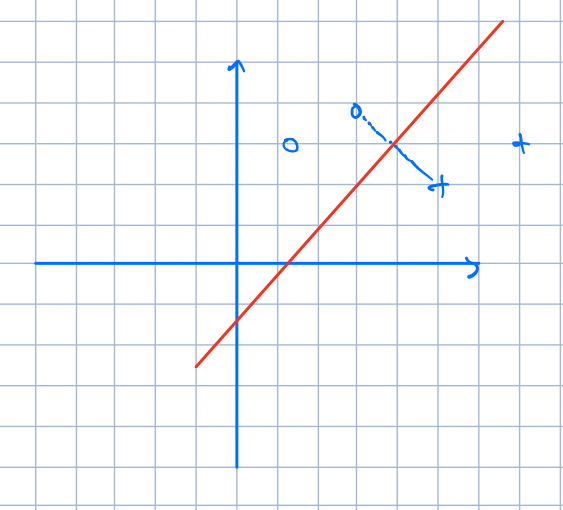
显然,看了上面的表述,我们应该知道决定这个超平面长什么样子的数据点只有那么几个,就是那些离超平面更近的点。下面开始将这个问题表述为一个最优化问题。
最优化问题的推导
我们想要寻找的超平面是\[ \begin{equation} w^Tx + b = 0 \end{equation} \]
对于所有的正例,希望\(w^Tx_i + b > 0\);反之,\(w^Tx_i + b < 0\)。其中,w和b是我们要求的参数。
1.0版本问题
最初的问题可以表述为
\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ margin(w,b) \\ s.t. \ \ \ 分类器将每一个数据点都分类正确 \\ \ \ \ \ \ \ \ \ margin(w,b) = \mathop{min}\limits_{i=1,2,...,n}distance(x_i, w, b) \end{equation} \]
1.1版本问题
我们定义标签\(y=+1/-1\),分别代表正例和负例。那么分类器将每一个数据点都分类正确这件事情相当于\(y_i(w^Tx_i+b) > 0\),更新一下问题表述:
\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ margin(w,b) \\ s.t. \ \ \ y_i(w^Tx_i+b) > 0 \\ \ \ \ \ \ \ \ \ margin(w,b) = \mathop{min}\limits_{i=1,2,...,n}distance(x_i, w, b) \end{equation} \]
2.0版本问题
\(distance\)代表每一个数据点到超平面的距离,在这里希望能将它用参数表示出来。假设超平面上的有一个数据点\(x^1\),它是个向量。那么对于它来说,显然有\[ \begin{equation} w^Tx^1 + b = 0 \end{equation} \]
现在超平面外有一点\(x^*\),也是向量形式。那么\((x^*-x_1)\)是两个向量的相减形式,记为\(p\)。超平面的法向量为\(w\),将\(p\)往\(w\)上投影的向量的模就是空间上点\(x^*\)到超平面的距离。用线性代数学过的知识表述,先求投影向量:\[ \begin{equation} \frac{w^Tp}{w^Tw}w = \frac{w^T(x^*-x_1)}{w^Tw}w=\frac{w^Tx^*-w^Tx_1}{w^Tw}w \end{equation} \]
又由(5)式,上述的式子再可以表述为
\[ \begin{equation} \frac{w^T(x^*-x_1)}{w^Tw}w=\frac{w^Tx^*+b}{w^Tw}w \end{equation} \]
好的,已经求出投影向量,接下来求投影向量的模。\(\frac{w^Tx^*+b}{w^Tw}\)是个标量,换言之,求(7)这个向量的模得到:
\[ \begin{equation} \frac{|w^Tx^*+b|}{w^Tw}\left\|w\right\| \end{equation} \]
而\(w^Tw\)=\(\left\|w\right\|^2\),因此最终可以写成:\[ \begin{equation} distance(x^*,w,b) = \frac{|w^Tx^*+b|}{\left\|w\right\|} \end{equation} \]
接下来更新问题表述:
\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ margin(w,b) \\ s.t. \ \ \ y_i(w^Tx_i+b) > 0 \\ \ \ \ \ \ \ \ \ margin(w,b) = \mathop{min}\limits_{i=1,2,...,n}\frac{|w^Tx_i+b|}{\left\|w\right\|} \end{equation} \]
2.1版本问题
其中,\(y_i(w^Tx_i+b) > 0\)与\(|w^Tx_i+b|\)又是等价的,所以问题可以精简为:\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ margin(w,b) \\ s.t. \ \ \ margin(w,b) = \mathop{min}\limits_{i=1,2,...,n}\frac{y_i(w^Tx_i+b)}{\left\|w\right\|} \end{equation} \]
3.0版本问题
这一步是最重要的变换了,整个推导过程我一直卡着的点就是这里。我想用我所理解的说一下这个。
- 超平面\(w^Tx+b=0\)能将一个空间分为两个部分,将某个向量\(x_i\)代入\(w^Tx+b\)中若是得到\(>0\)或者\(<0\)说明\(x_i\)在超平面的某一侧。
- 将超平面\(w^Tx+b=0\)的参数\(w,b\)同时缩放,比如都变大3倍或者都变小3倍,这个超平面是不会变的,它还是处于空间中的那个位置。这一点如果不理解可以在二维空间中划一条线比如\(3x_1+2x_2-1=0\),对等式左右乘3得到新的等式仍然表述二维空间的那条线。
- 上面两个都是前提。虽然对超平面\(w^Tx+b=0\)的参数\(w,b\)同时缩放了,超平面还是那个超平面,但是有一点却改变了。就是将某个向量\(x_i\)代入\(w^Tx+b\)中计算得到的值。想象一下,这个超平面\(3x_1+2x_2-1=0\),现在有一个点(1,2)代入得到值6,但是如果将参数都放大3倍,再将点重新代入计算,得到的值也放大了3倍变为18。
- 既然参数怎么放大缩小超平面都不会变,那么何不为了方便计算,将\(w,b\)缩放到特定的值\(w^*,b^*\),使得对于那些数据点,有\[\begin{equation}\mathop{min}\limits_{i=1,2,...,n}y_i((w^*)^Tx_i+b^*)=1\end{equation}\]这是做得到的,假设数据点中距离超平面的最近的那个点为\(x^*\),离超平面的距离为\(l\)。只要将参数缩放\(l\)倍,不就满足了(12)式。
这样一来,原来的问题就表述为:\[ \begin{equation} \mathop{max}\limits_{w^*,b^*} \ \ \ \frac{1}{\left\|w^*\right\|} \\ s.t. \ \ \ \mathop{min}\limits_{i=1,2,...,n} \ y_i((w^*)^Tx_i+b^*)=1 \end{equation} \]
为了和原来的形式统一,还是写为\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ \frac{1}{\left\|w\right\|} \\ s.t. \ \ \ \mathop{min}\limits_{i=1,2,...,n} \ y_i(w^Tx_i+b)=1 \end{equation} \]
4.0版本问题
这里的约束条件还是有些不友好,能不能将\(min\)这个条件去掉。第一反应是用以下不等式来替换:\[ \begin{equation} for \ (x_i,y_i) \in D \ \ \ y_i(w^Tx_i+b)>=1 \end{equation} \]
遗憾的是,两者并不是简单的等价关系,或者说原来的约束条件是能推出(15)的,但是反过来并不行。比如,所有对于所有数据点\(\mathop{min}\limits_{i=1,2,...,n} \ y_i(w^Tx_i+b)=1.26\),它是满足(15)的,但是推不出原来的约束条件。
但是,我们现在可以证明假如可以求出一组最优参数\(w,b\),它必然能满足\(\mathop{min}\limits_{i=1,2,...,n} \ y_i(w^Tx_i+b)=1\)。
这是为什么?
设已经求出的最优解为\(w_1, b_1\),但是\(\mathop{min}\limits_{i=1,2,...,n} \ y_i(w_1^Tx_i+b_1)=1.26\)。我们可以很肯定的说这组必然不是最优解,因为我们希望优化的目标为\(\frac{1}{\left\|w\right\|}\),要令其最大。现在取这组最优解时得到目标值为\(\frac{1}{\left\|w_1\right\|}\),但是\(\frac{1}{\left\|\frac{w_1}{1.26}\right\|}\)显然比\(\frac{1}{\left\|w_1\right\|}\)更大,因此现在取到的\(w_1, b_1\)根本不是最优解。最优的参数必然能满足\(\mathop{min}\limits_{i=1,2,...,n} \ y_i(w^Tx_i+b)=1\).
所以,我们可以放心地用(15)代替原来的约束条件。更新问题表述后变为:\[ \begin{equation} \mathop{max}\limits_{w,b} \ \ \ \frac{1}{\left\|w\right\|} \\ s.t. \ \ \ \ y_i(w^Tx_i+b) \ >= \ 1 \end{equation} \]
4.1版本问题
为了符合凸优化数学问题的通常形式,以及方便后续的计算,最终的问题表述为:\[ \begin{equation} \mathop{min}\limits_{w,b} \ \ \ \ \frac{\left\|w\right\|^2}{2} \\ s.t. \ \ \ \ y_i(w^Tx_i+b) \ >= \ 1 \end{equation} \]
好了,我去看凸优化了。。。