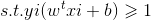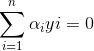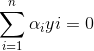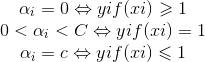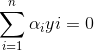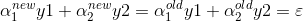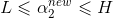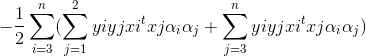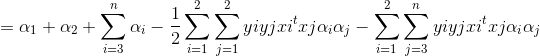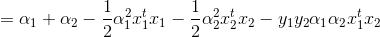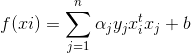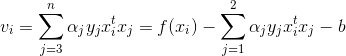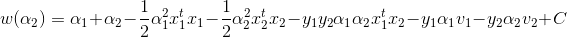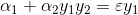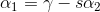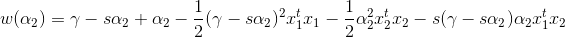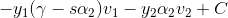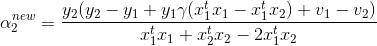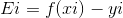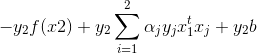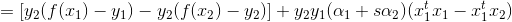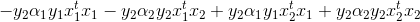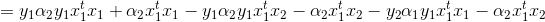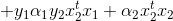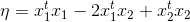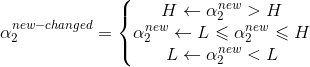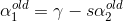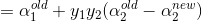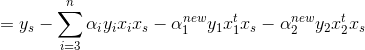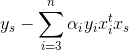1.SMO算法简介
SMO算法又称序列最小优化,是John Platt发布的的一种训练SVM的强大算法,SMO算法的思想是将大的优化问题转换为多个小优化问题,这些小的优化往往很容易求解,并且对他们进行顺序求解和作为整体求解的结果是完全一致的。SMO算法的目标是求出一些列alpha和b,一旦求出alpha,我们的超平面w的系数便得到,我们就可以利用超平面来进行分类了。
SMO算法的工作原理是每次循环中选择两个alpha进行优化,先选择一个αi,然后固定αi之外的其他参数,求αi上的极值,由于存在零和约束,所以修改αi时,我们也需要修改一个αj,所以我们选择两个变量αi,αj进行优化,并固定其他参数,在参数初始化后,SMO不断执行下列两个步骤直到收敛:
·选取一对需要更新的αi,αj
·固定αi,αj之外的参数,求解获得新的αi,αj
首先在不满足KKT条件的集合中选取αi,αj,其次SMO采取了一种启发式,使选取的两变量对应的间隔越大越好,直观的解释是,这两个变量有很大的差别,与对两个相似的变量进行更新对比,对他们更新会带给目标函数值更大的变化。
2.SMO算法推导
下面开始推导SMO的算法公式,过程中会涉及到松弛因子的引入和alpha更新规则的内容,将在下一篇文章给出详细证明,这里主要对整体框架进行推导。
先整理一下SMO算法的思路:
1)选取αi,αj,固定两个参数外的其他参数
2)重写约束 αi + αj = k αi≥0,αj≥0
3)由上式消去一个αj,从而得到αi的单变量二次规划,αi≥0,从而求出αi≥0,再由约束求出αj
4)不断更新αi,αj到α收敛,从而通过计算得到w
4)对于支持变量而言:有yi(w.Txi+b)=1,在w已知的情况下,求解b
5)通过得到的w和b,推出分割超平面,从而进行分类
proof:
明确目标(寻找最优超平面):
优化的目标函数(寻求最大间隔):
通过拉格朗日乘子构造拉格朗日函数(转化为无约束问题)并对w,b求偏导:
对偶问题(通过对偶问题优化算法计算速度):
==>对于上述计算,我们都是假定数据100%线性可分,但是现实生活中,我们难免会有一些数据有偏差,所以这里我们引入松弛变量(优化目标不变的情况下增加模型适应性),允许数据可以处于超平面错误的一侧或处于间隔带之间,此时优化目标不变,约束条件有所改变:
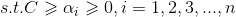
从而根据KKT条件(选择以及更新α的准则):
大于等于1意味着在正常分类范围,等于1意味着对应点为支持向量,小于等于1意味着在间隔之间.通过加入松弛变量,我们得到了新的KKT条件,因此我们需要对不满足KKT条件的αi进行更新。
==>另一个约束条件(简化约束)
∴
通过新的约束,我们可以先求α2的值,再反过来求α1的值,简化计算,但是根据前面的约束,我们需要确定的更新范围,上界H下界L假设:
依据简化约束,我们需要分两种情况讨论(其实是四种),y1=y2和y1≠y2:
y1≠y2时:
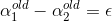
∴ L=max(0,-ε) H=min(C,C-ε)
y1=y2时:
∴ L=max(0,ε-C) H=min(C,ε)
得到界限后,我们推导迭代公式(tips:yiyi=1):
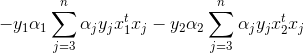
上式我们分离出了α1和α2,通过代换,即可导出α2的二次函数,变为单变量二次规划问题.
为了简化表达,我们定义:
从而目标函数简化为:
这里C为常数,因为对于α1和α2而言,求导时其他参数均为0,所以统一为常数C.
由前面简化约束条件:
两边同乘y1:
令y1y2=S,εy1=r:
带入w(α2),得到关于α2的单变量二次函数:
下面对α2求偏导:
令偏导数为0,并将s=y1y2带入:
继续简化,令:
又:
将上述条件带入α2new的更新式,这里我们先处理上面的部分:

再结合分母:
我们得到α2的更新公式:
现在根据前面的范围规则对α2进行调整:
得到α2后,我们利用简化约束即可求α1:
∴
这样α1,α2就得到了,接下来就是截距项b的求解.
当αs的更新值在0-C之间时,根据KKT条件可以得到对应的点是支撑向量,从而满足以下条件:
针对前两项化简:
将前两项简化的结果带入b中,并将s换为1,2,就得到了截距项b1和b2了:
根据b的更新法则:
通过以上步骤,就成功更新一组α1,α2和b了,SMO算法之所以高效是因为在固定其他参数情况下,仅优化两个参数非常的简便,基于这样的更新步骤,SMO算法不断更新乘子α,直到达到循环条件或α都无法优化即都满足KKT条件时,我们就找到了目标函数的最优值.
总结:
通过不断迭代直到收敛,得到αi和b,通过
就能得到超平面所需的全部参数,这样我们就可以用超平面进行分类了。SMO的算法大致内容就是这些,但是这其中有一些乐观的假设,下一篇文章就将本文中涉及到的松弛因子的引入和α范围规则进行证明,从而对SMO有更深的理解。还有就是《机器学习实战》书中一些代码和本文的SMO算法有一些小差异,例如对不满足KKT条件的判断,以及α的选择问题,之后也都会写到。