支持向量机SVM算法推导及实现

支持向量机

1.前言

支持向量机(Support Vector Machine)是常用的分类模型，其核心思想是求解超平面使得数据集分成两堆，其中一堆是正例，另一堆是反例。但能够将数据集D分开的超平面存在很多个，如下图所示，我们应该如何选择最优超平面呢？

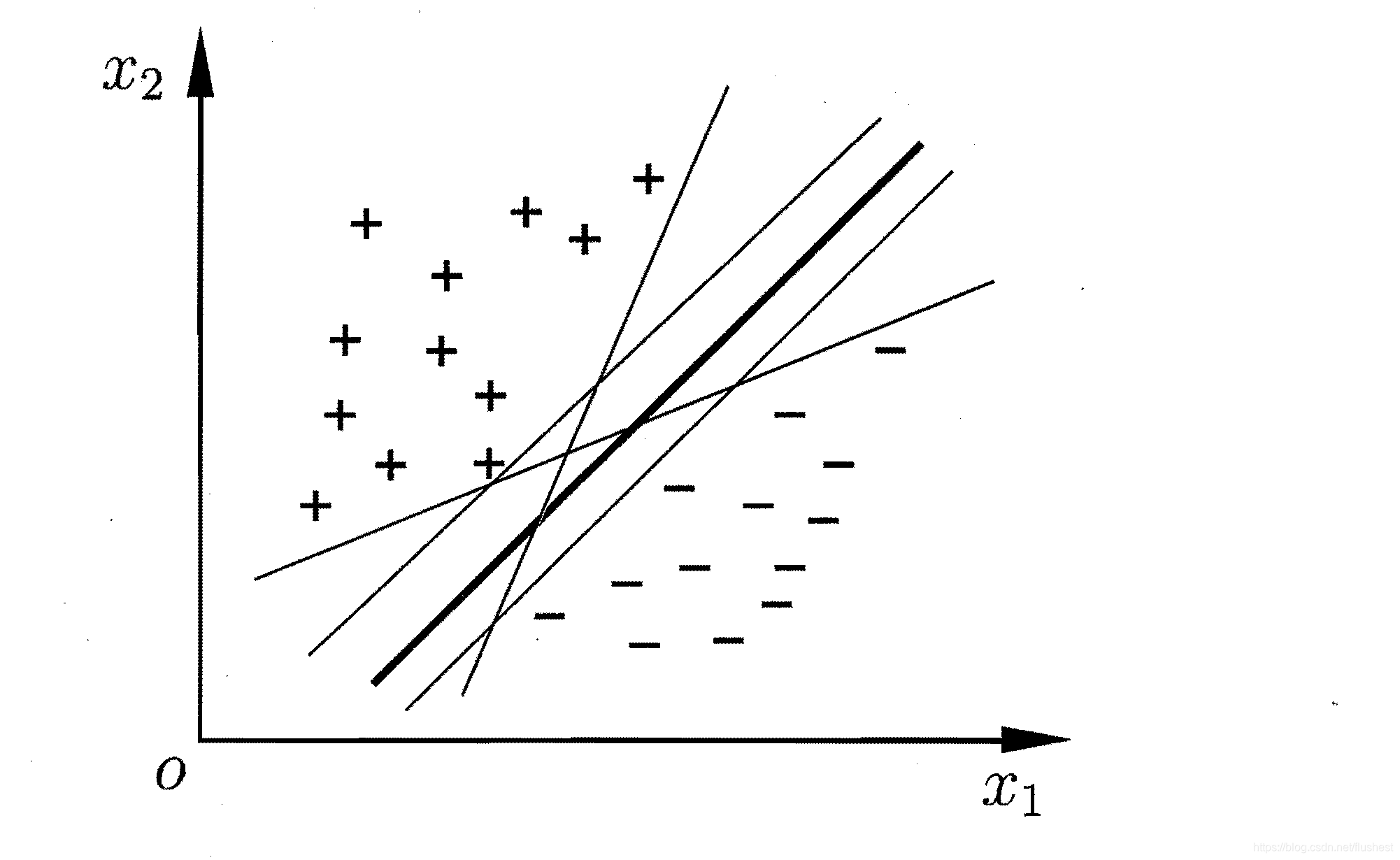
从直觉上看，粗线应该是最优超平面，因为正反例样本距离超平面最远、间隔最大。间隔越大，说明分类越准确，置信度越高。

在样本空间中，划分超平面可以通过如下线性方程来描述：
$\omega ^T \mathbf{x}+b=0$
其中， $\mathbf{\omega} = (\omega_1,\omega_2,...,\omega_k)$为法向量，决定了超平面方向；b为位移项，决定了超平面与原点之间的距离。显然，正反例样本到超平面的距离与法向量、位移项有关。于是做出如下定义：

对于任意一点 $(x_i,y_i)$且 $y_i \in \{-1.1\}$，其到超平面 $\omega ^T \mathbf{x}+b=0$的距离可定义为 $y_i(\omega ^ Tx_i+b)$。选择好划分超平面后，正反两类样本中到超平面距离最近的样本点被称为支持向量，其到超平面的距离被称为间隔，如下图。

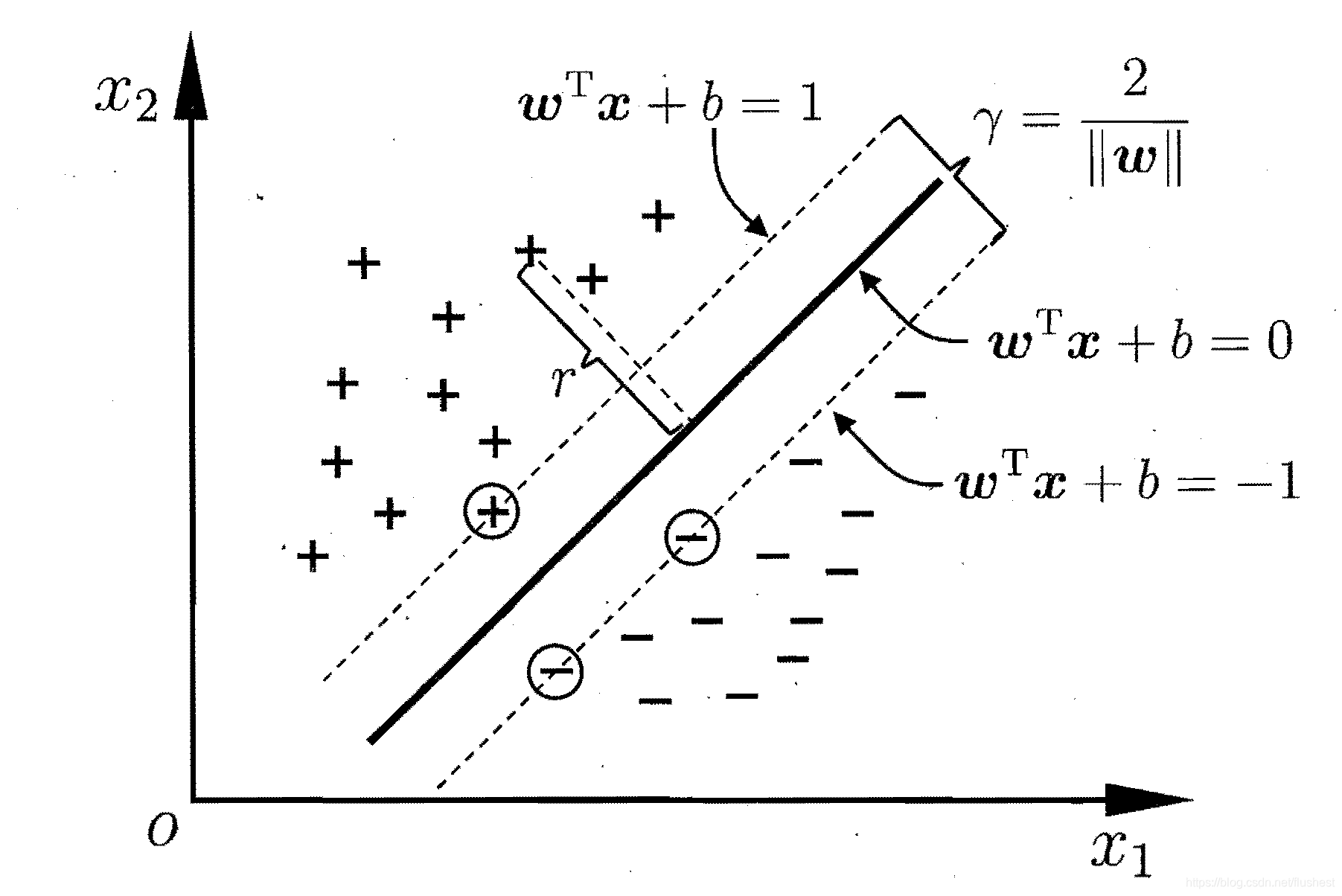
其中带圆圈的样本为支持向量，虚线之间的空白部分为间隔。间隔有两种定义：

• 函数间隔
  $\gamma = y_i(\omega^T x_i + b)$

• 几何间隔
  $\hat{\gamma}=\frac{\gamma}{||\omega||}$

函数间隔易受 $||\omega||$影响，但超平面方程同除 $|| \omega ||$，超平面不变，其间隔也应该不变，所以引入几何间隔来表示点到超平面距离。

2.线性可分支持向量机

线性可分是指一定存在某一个超平面使得数据集完全正确地分成正反两类，前言中图片展示的就是一个线性可分数据集。当然也存在一些数据集，比如异或关系的数据集，无法由一个平面来进行划分，可能需要曲面才能够划分，这样的数据集称为线性不可分。

线性可分支持向量机正是用来解决线性可分数据集分类问题的，其原始问题形式如下：
$\begin{aligned} &\max_{\omega,b} \space \space \hat{\gamma}\\ &s.t. \space y_i(\omega^Tx_i+b) \ge \gamma,i=1,2,...,n \end{aligned}$
又因为 $\hat{\gamma}=\frac{\gamma}{||\omega||}$，不妨取 $\gamma=1$，通过调整 $\omega$来调整几何间隔。于是问题等价于
$\begin{aligned} & \max_{\omega,b} \space \space \frac{1}{||\omega||}\\ & s.t. \space y_i(\omega^Tx_i+b) \ge 1,i=1,2,...,n \end{aligned}$
将上式转化为最小值问题：
$\begin{aligned} & \min_{\omega,b} \space \space \frac{1}{2}||\omega||^2\\ & s.t. \space y_i(\omega^Tx_i+b) \ge 1,i=1,2,...,n \end{aligned}$
此时由于这是一个条件约束极值问题，转化为对偶问题：

• 拉格朗日函数

  对于不等式约束条件下最小值拉格朗日函数通用形式为
  $\begin{aligned} &\min_{x} f(x)\\ &s.t. \space h_i(x) \lt 0,\\ & g_i(x)=0,i=1,...,n\\ &\Rightarrow L(x,a,\lambda)=f(x)+\sum_{i=1}^na_ih_i(x) + \sum_{i=1}^n \lambda_ig_i(x) \space and \space a_i \ge 0 \end{aligned}$
  于是原始问题拉格朗日函数为
  $L(\omega,b,a) = \frac{1}{2}||\omega||^2 + \sum_{i=1}^n a_i[1-y_i(\omega^Tx_i+b)], \space a_i \ge 0$

• 原始问题可转化为极小极大问题

  对于拉格朗日函数 $L(x,a,\lambda)=f(x)+\sum_{i=1}^na_ih_i(x) + \sum_{i=1}^n \lambda_ig_i(x) \space and \space a_i \ge 0$有，
  $\max_{a_i \ge 0,\lambda_i}L(x,a,\lambda) = \left\{ \begin{aligned} & f(x),&h_i(x)\gt 0 \space or \space g_i(x) \not = 0\\ & \infin, &h_i(x)\le 0 \space and \space g_i(x)=0 \end{aligned} \right.$
  显然，当不满足约束条件时，拉格朗日函数第二部分或者第三部分最大值趋于无穷大；当满足约束条件时，拉格朗日函数最大值为函数值f(x)，于是取其最小值得
  $\min_{\omega,b} \max_{a_i \ge 0} L(\omega,b,a)$

• 对偶问题极大极小问题
  $\max_{a_i \ge 0} \min_{\omega, b} L(\omega, b, a)$
  令 $\psi(a)=\min_{\omega,b} L(\omega,b,a)$，拉格朗日函数求偏导得
  $\begin{aligned} &\frac{\partial L}{\partial \omega}=\omega - \sum_{i=1}^na_iy_ix_i\\ &\frac{\partial L}{\partial b}=-\sum_{i=1}^na_iy_i \end{aligned}$

  令偏导为0，可得 $，\omega=\sum_{i=1}^na_iy_ix_i，\sum_{i=1}^na_iy_i=0$，带入 $\psi(a)$得
  $\psi(a)=-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n a_iy_i \cdot a_jy_j \cdot x_ix_j+\sum_{i=1}^na_i$
  于是，问题转化为
  $\begin{aligned} &\max_a \space \psi(a) \\ &s.t. \sum_{i=1}^na_iy_i=0,\\ &\space \space \space \space \space \space a_i \ge 0,i=1,2,...,n \end{aligned}$
  将上述问题转化为最小值问题得
  $\begin{aligned} &\min_a \space \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n a_iy_i \cdot a_jy_j \cdot x_ix_j-\sum_{i=1}^na_i \\ &s.t. \sum_{i=1}^na_iy_i=0,\\ &\space \space \space \space \space \space a_i \ge 0,i=1,2,...,n \end{aligned}$
  由此，得出线性支持向量机的最终问题形式，这种形式的极值问题采用SMO算法求解，在后面会谈到。最终得到的决策规则形式为
  $f(x)=sign(\sum_{i=1}^na_iy_ix_i \cdot x + b)$
  其中，选择支持向量 $0 \lt \alpha_i \lt C$，则 $b=y_i - \sum_{j=1}^na_jy_jx_j \cdot x_i$

3.线性支持向量机

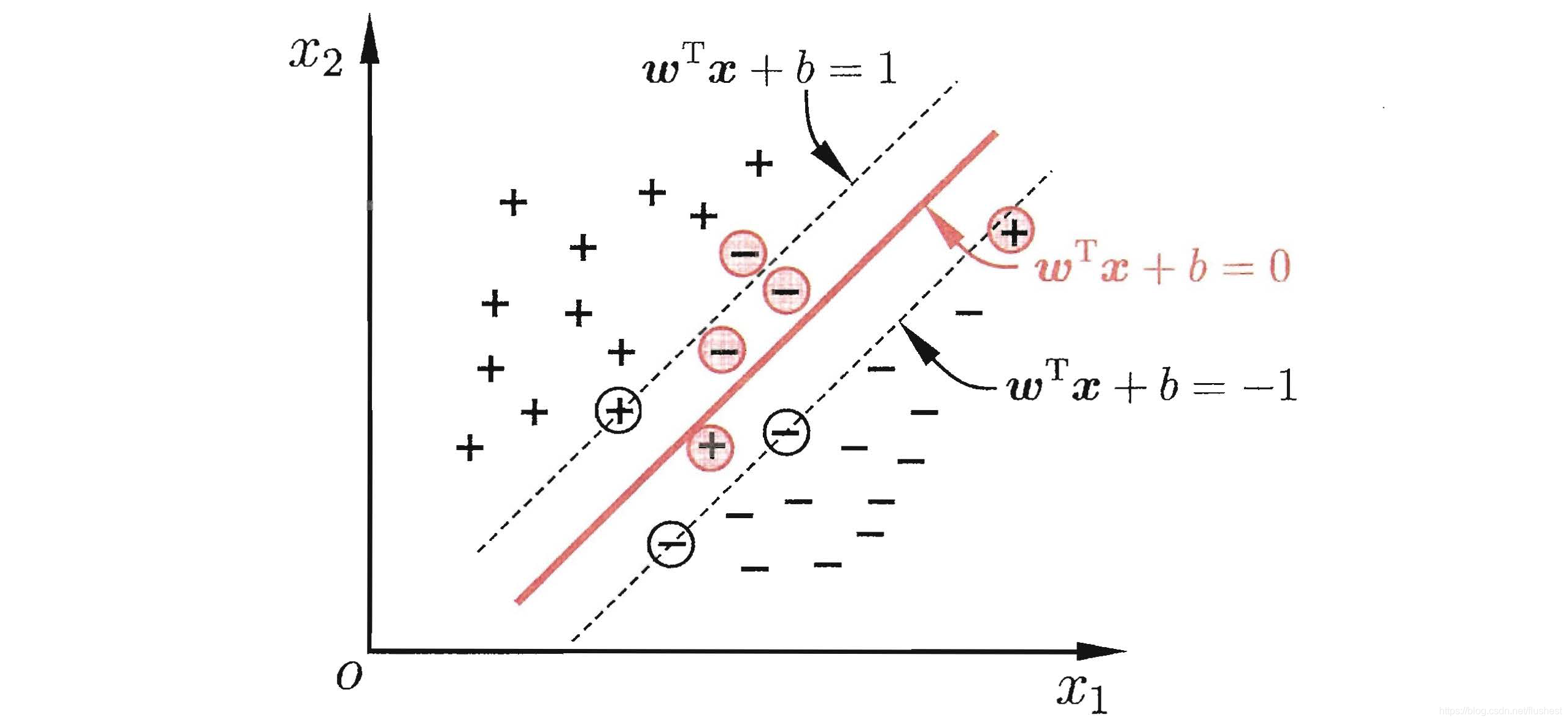
对于线性不可分数据集，如果存在一个划分超平面使得大部分点都能正确划分，只有比较少的点错误，那么可以使用线性支持向量机解决这个问题。在前面线性可分支持向量机中讲过，数据集中所有点到超平面的距离都应该大于函数间隔，但对于线性不可分数据集而言，定义软间隔，在函数间隔的基础上设置松弛变量，使分类器能够接受一定的错误分类。如下图所示，红色圆圈中的样本点都是存在松弛变量的，用形式化公式表示 $，y_i(\omega^Tx_i+b)\ge1-\xi_i，\xi_i \ge 0$，其中 $\xi_i$为松弛变量。显然，我们希望松弛变量越小越好。

于是，线性支持向量机原始问题为
$\begin{aligned} & \min_{\omega,b,\xi} \space \space \frac{1}{2}||\omega||^2+C\sum_{i=1}^n\xi_i\\ & s.t. \space y_i(\omega^Tx_i+b) \ge 1-\xi_i,\xi_i \ge 0,i=1,2,...,n \space and \space C>0 \end{aligned}$
转化为对偶问题

• 拉格朗日函数
  $L(\omega,b,\xi,a,\mu)=\frac{1}{2}||\omega||^2+C\sum_{i=1}^n\xi_i+\sum_{i=1}^na_i[1-\xi_i-y_i(\omega^Tx_i+b)]-\sum_{i=1}^n\mu_i\xi_i$

• 原始问题极小极大问题
  $\min_{\omega,b,\xi} \max_{a_i \ge 0, \mu_i \ge 0} L(\omega,b,\xi,a,\mu)$

• 对偶问题极大极小问题

$\max_{a_i \ge 0, \mu_i \ge 0} \min_{\omega,b,\xi} L(\omega,b,\xi,a,\mu)$

​ 拉格朗日函数求偏导分别为
$\begin{aligned} &\frac{\partial L}{\partial \omega}=\omega - \sum_{i=1}^na_iy_ix_i\\ &\frac{\partial L}{\partial b}=-\sum_{i=1}^na_iy_i\\ &\frac{\partial L}{\partial \xi_i}=C-a_i-\mu_i \end{aligned}$
​ 令偏导为0，并带入原问题有
$\begin{aligned} &\min_a \space \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n a_iy_i \cdot a_jy_j \cdot x_ix_j-\sum_{i=1}^na_i \\ &s.t. \space \sum_{i=1}^na_iy_i=0,\\ &\space \space \space \space \space \space 0 \le a_i \le C,i=1,2,...,n \end{aligned}$
从另一个角度看，原始问题中 $\frac{1}{2}||\omega||^2$表示第二范数，属于正则项， $C\sum_{i=1}^m\xi_i$表示经验风险，其中 $\xi_i=\max\{0,1-y_i(\omega^Tx_i+b)\}$表示hinge损失函数。当然损失函数可以换成其他的，那么相应地转换为其他模型算法，后续再谈。

4.非线性支持向量机

​ 之前介绍的算法都不能解决真正的线性不可分数据集问题。考虑到机器学习算法效果是依赖于数据表现形式的，换个角度思考线性不可分问题，在原始维度空间无法找到超平面进行线性划分，但是当进行维度变换时，一定能够找到一个更高维度特征空间能够进行线性划分，这是由模式识别理论证明过的，如下图所示。数据集在直角坐标系中无法用直线完全正确地划分，但是当转换为极坐标系时，却能够进行线性划分。

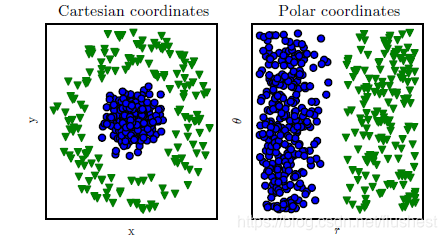
​ 那么如何进行维度变换呢？从之前导出的问题最终形式可以看出，样本数据通过 $x_i \cdot x_j$形式整合到模型算法中。于是假设通过维度变换后样本数据整合形式为 $\phi(x_i) \cdot \phi(x_j)$，但是由于维度变换后特征向量维度不定，直接使用內积计算效率比较低。举例来说，原始样本空间中 $x=[x_1,x_2,...,x_n]^T$，经过维度变换后 $\phi(x) =[x_1x_1,x_1x_2,...,x_1x_n,...,x_nx_1,...,x_nx_n]$，于是 $k(x,l)\phi=(x) \cdot \phi(l)=\sum_{i=1}^n\sum_{j=1}^n(x_ix_j)(l_il_j)=\sum_{i=1}^n(x_il_i) \sum_{j=1}^n(x_jl_j)=(x^Tl)^2$。因此，核函数 $K(x,l)$时间复杂度为O(n)优于升维后內积。

（1）核函数定义

​ 在举例中 $k(x,l)=(x^Tl)^2$就是一个核函数，核函数指能够简化经过隐式维度变换后空间內积计算的函数。以下对核函数做出定义:

令 $\chi$为输入空间， $k(\cdot,\cdot)$是定义在 $\chi \times \chi$上的对称函数，则K是核函数当且仅当对于任意数据 $D=\{x_1,x_2,...,x_m\}$有，“核矩阵”K始终是半正定的：
$K=\left[ \begin{matrix} k(x_1,x_1)&k(x_1,x_2)&...&k(x_1,x_m)\\ k(x_2,x_1)&k(x_2,x_2)&...&k(x_2,x_m)\\ .&.&...&.\\ .&.&...&.\\ .&.&...&.\\ k(x_m,x_1)&k(x_m,x_2)&...&k(x_m,x_m) \end{matrix} \right]$

（2）常用核函数

​ 在举例中先确定维度变换公式，再计算出核函数，但是在现实问题中往往不能够很容易地确定维度变换公式。所以人们常常从归纳总结出的常用核函数中，根据不同的问题和参数选择不同的核函数。常用核函数如下：

• 多项式核函数：适合正交归一化数据
  $k(x,z)=(x \cdot z+1)^p$

• 高斯核函数：径向基核函数，适用性广，鲁棒性好，对参数敏感
  $k(x,z)=exp\{-\frac{||x-z||^2}{2\delta^2}\}$

• ANOVA核函数：适用于多维回归问题
  $k(x,z)=exp(-\delta(x^k-y^k)^2)^d$

• sigmoid核函数：广泛应用于深度学习
  $k(x,z)=tanh(\alpha x \cdot z+c)$

• 对数核：多用于图像分割
  $k(x,z)=-log(1+||x-z||^d)$

• 直方图交叉核：多用于图像分类
  $k(x,z)=\sum_{k=1}^n\min\{x_k,z_k\}$

5.SMO算法

​ SMO算法是一种启发式算法，用于快速解决凸二次优化问题。其基本思路是，如果所有变量都能够满足最优化问题KKT条件，那么最优化问题就能够求解出。选择所有变量中最不符合KKT条件的变量 $\alpha_1$,另一个变量 $\alpha_2$随着 $\alpha_1$的变化而变化，选择使 $\alpha_1$变化最大的 $\alpha_2$，其他所有变量固定不变。由此求解这个二次优化问题，不断逼近最优解。

算法推导过程：

令 $K=\sum_{i=3}^na_iy_i$，并代入约束条件 $\sum_{i=1}^n\alpha_iy_i=0$得
$\alpha_2y_2 = (-\alpha_1y_1 - K)$
对偶问题展开可得
$\min_{\alpha} \frac{1}{2}(\alpha_1y_1x_1+\alpha_2y_2x_2 + \sum_{i=3}^n\alpha_iy_ix_i)(\alpha_1y_1x_1+\alpha_2y_2x_2 + \sum_{j=3}^n\alpha_jy_jx_j) - \sum_{i=1}^n\alpha_i\\ \Rightarrow \min_{\alpha}\frac{1}{2}[\alpha_1^2k(x_1,x_1)+2\alpha_1y_1\alpha_2y_2k(x_1,x_2)+\alpha_2^2k(x_2,x_2) \\ +2(\alpha_1y_1x_1+\alpha_2y_2x_2)\sum_{i=3}^n\alpha_iy_ix_i+\sum_{i=3}^n\sum_{j=3}^n \alpha_iy_i \cdot \alpha_jy_j \cdot x_ix_j] - \sum_{i=1}^n\alpha_i\\$
令 $L=\sum_{i=3}^n\sum_{j=3}^n \alpha_iy_i \cdot \alpha_jy_j \cdot x_ix_j,\space P=\sum_{i=3}^n\alpha_iy_ix_i$，并代入对偶问题得
$\min_{\alpha} \frac{1}{2}\{\alpha_1^2k(x_1,x_1)-2(\alpha_1^2+K\alpha_1y_1)k(x_1,x_2)+(\alpha_1y_1+K)^2k(x_2,x_2)+2[\alpha_1y_1(x_1-x_2)-Kx_2]P+L\}-\sum_{i=1}^n\alpha_i\\ \Rightarrow \min_{\alpha}\frac{1}{2}\{\alpha_1^2[k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)]+\alpha_1[-2Ky_1k(x_1,x_2)+2Ky_1k(x_2,x_2)+2y_1(x_1-x_2) \cdot P - 2(1-y_1/y_2)]\}$
对 $\alpha_1$求导可得
$\begin{aligned} \alpha_1^{new}&=\frac{Ky_1k(x_1,x_2)-Ky_1k(x_2,x_2)-y_1(x_1-x_2) \cdot P + (1-y_1/y_2)}{k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)}\\ &=\frac{-y_1(\alpha_1y_1+\alpha_2y_2)[k(x_1,x_2)-k(x_2,x_2)]-y_1(x_1-x_2)\sum_{i=1}^n\alpha_iy_ix_i+y_1(x_1-x_2)(\alpha_1y_1x_1+\alpha_2y_2x_2)+1-y_1y_2}{k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)}\\ &=\frac{\alpha_1[k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)]-y_1[\sum_{i=1}^n\alpha_iy_ik(x_1,x_i)-\sum_{i=1}^n\alpha_iy_ik(x_2,x_i)]+1-y_1y_2}{k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)}\\ &=\alpha_1-\frac{y_i[\sum_{i=1}^n\alpha_iy_ik(x_1,x_i)-\sum_{i=1}^n\alpha_iy_ik(x_2,x_i)]-1+y_1y_2}{k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)} \end{aligned}$
进一步地，因为 $，k(x_1-x_2,x_1-x_2)=k(x_1,x_1)-2k(x_1,x_2)+k(x_2,x_2)，y_1^2=1$有
$\begin{aligned} \alpha_1^{new}&=\alpha_1-\frac{y_1[\sum_{i=1}^n\alpha_iy_ik(x_1,x_i)-\sum_{i=1}^n\alpha_iy_ik(x_2,x_i)]-(y_1^2-y_1y_2)}{k(x_1-x_2,x_1-x_2)}\\ &=\alpha_1-\frac{y_1\{[\sum_{i=1}^n\alpha_iy_ik(x_1,x_i)+b-y_1]-[\sum_{i=1}^n\alpha_iy_ik(x_2,x_i)+b-y_2]\}}{k(x_1-x_2,x_1-x_2)} \end{aligned}$
令 $，\eta = k(x_1-x_2,x_1-x_2)，E_i=g(x_i)-y_i=\sum_{j=1}^n\alpha_jy_jk(x_i,x_j)+b-y_i$，其中 $E_i$表示预测值与真实值之间误差。于是
$\alpha_1^{new} = \alpha_1^{old}-\frac{y_1(E_1-E_2)}{\eta}$

$\alpha_2^{new} = y_2[(\alpha_1^{old}-\alpha_1^{new})y_1+\alpha_2^{old}y_2]=\alpha_2^{old}+y_1y_2(\alpha_1^{old}-\alpha_1^{new})$

进一步地， $\alpha_1,\alpha_2$应该满足约束条件 $0 \le \alpha_1,\alpha_2 \le C$，于是优化后的 $\alpha_1^{new},\alpha_2^{new}$在二维空间中图像表示如下:

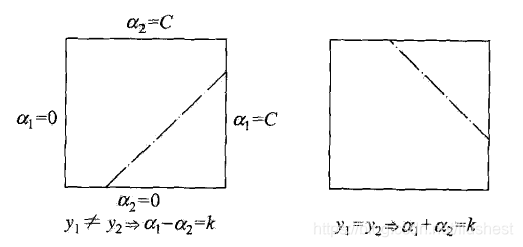
故，取L与H分别为 $\alpha_1^{new}$约束下界和上界，当 $y_1 \not= y_2$时
$L=\max\{0,\alpha_1^{old}-\alpha_2^{old}\},\space H=\min\{C,C+\alpha_1^{old}-\alpha_2^{old}\}$
当 $y_1=y_2$时， $L=\max\{0,\alpha_1^{old}+\alpha_2^{old}-C\},\space H=\min\{C,\alpha_1^{old}-\alpha_2^{old}\}$

因此，
$\alpha_1^{new}= \begin{cases} &H,&\alpha_1^{new} \gt H\\ &\alpha_1^{new},&L\le \alpha_1^{new} \le H\\ &L,&\alpha_1^{new}<L \end{cases}$

$\alpha_2^{new} = y_2[(\alpha_1^{old}-\alpha_1^{new})y_1+\alpha_2^{old}y_2]=\alpha_2^{old}+y_1y_2(\alpha_1^{old}-\alpha_1^{new})$

接下来，问题关键是如何选取变量 $\alpha_1,\alpha_2$,先选取违反KKT条件的变量作为 $\alpha_1$，再选取 $|E_1-E_2|$最大的变量作为 $\alpha_2$。其中KKT条件为
$\begin{aligned} \alpha_i = 0 &\Rightarrow& y_ig(x_i) \ge 1\\ 0 \lt \alpha_i \lt C &\Rightarrow& y_ig(x_i)=1\\ \alpha_i=C&\Rightarrow&y_ig(x_i)\le1 \end{aligned}$
更新 $\alpha_1,\alpha_2$后，需要同时更新b，分以下情况：

• $\alpha_1,\alpha_2$中至少存在一个支持向量： $b=y_i - \sum_{j=1}^na_jy_jx_j \cdot x_i$，其中 $x_i$表示支持向量
• $\alpha_1,\alpha_2$均不是支持向量：令 $b_i=y_i - \sum_{j=1}^na_jy_jx_j \cdot x_i$，则 $b=(b_1+b_2)/2$

6.算法实现

import numpy as np
from math import *


class SVM(object):
    # 初始化超参数
    def __init__(self, C, kernel):
        self.C = C
        self.kernel = kernel

    # 计算g(x)值
    def g(self, x, alpha, b, trainMat, trainLabels):
        n = trainMat.shape()[0]
        return np.sum([alpha[i]*trainLabels[i]*self.kernel(x,trainMat[i]) for i in range(n)]) + b


    # 训练数据
    def train(self, trainMat, trainLabels):
        n,m = trainMat.shape()
        # 设置初值
        alpha = np.zeros((n,1))
        b = np.sum(trainLabels)/n

        # 循环训练
        while True:
            # 计算g(x)值
            G = np.array([self.g(trainMat[i], alpha, b, trainMat, trainLabels) for i in range(n)])
            # 满足KKT条件状态
            dis = np.multiarray(G, trainLabels)
            status = [ 1 if alpha[i]==0 and  dis[i] < 1 or 0< alpha[i] < self.C and dis[i] != 1 or alpha[i]==self.C and dis[i] > 1 else 0 for i in range(n)]

            # 均满足KKT条件
            if 0 == sum(status):
                break

            # 阿尔法变量1
            i = status.index(1)

            # 计算E
            E = G - trainLabels
            delta = [fabs(E[j] - E[i]) for j in range(n)]

            # 阿尔法变量2
            j = delta.index(max(delta))

            # 更新无约束最优解
            eta = self.kernel(trainMat[i]-trainMat[j], trainMat[i]-trainMat[j])
            aiNew = alpha[i] - trainLabels[i]*(E[i]-E[j])/eta

            # 约束更新
            if trainLabels[i] == trainLabels[j]:
                L = max(0, alpha[i]+alpha[j]-self.C)
                H = min(self.C, alpha[i]-alpha[j])
            else:
                L = max(0, alpha[i]-alpha[j])
                H = min(self.C, self.C+alpha[i]-alpha[j])

            if aiNew > H:
                aiNew = H
            elif aiNew < L:
                aiNew = L

            ajNew = alpha[j] + trainLabels[i]*trainLabels[j]*(alpha[i]-aiNew)

            # 更新alpha,b
            alpha[i] = aiNew
            alpha[j] = ajNew

            if 0<aiNew<self.C:
                b = trainLabels[i] - G[i] + b
            elif 0<ajNew<self.C:
                b = trainLabels[j] - G[j] + b
            else:
                b = (trainLabels[i] - G[i] + trainLabels[j] - G[j])/2 + b
        self.alpha = alpha
        self.b = b
        self.trainMat = trainMat
        self.trainLabels = trainLabels

    # 预测
    def predict(self, x):
        if self.g(x, self.alpha, self.b, self.trainMat, self.trainLabels) > 0:
            return 1
        else:
            return 0

参考资料

• https://blog.csdn.net/v_july_v/article/details/7624837
• 《机器学习》 - 周志华
• 《统计学习方法》 - 李航
• 《机器学习实战》

github代码地址https://github.com/flushest/machine-learning-practice