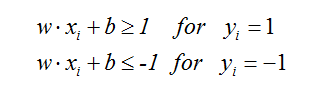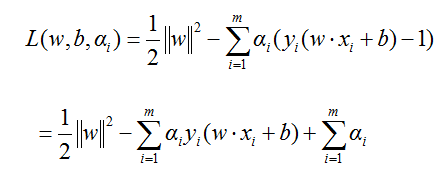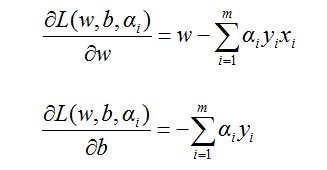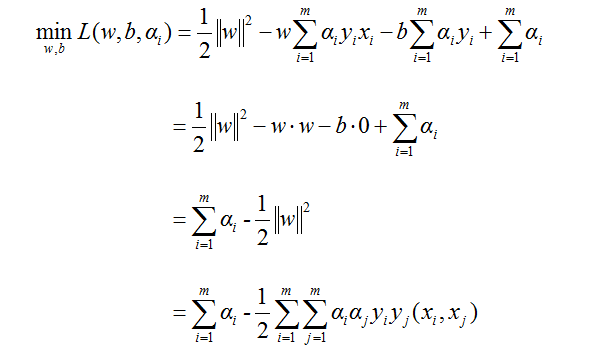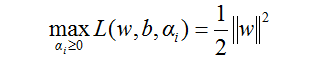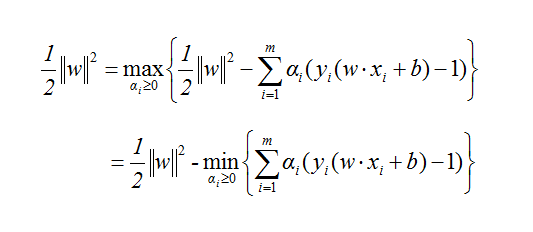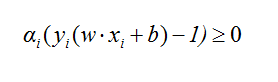支持向量机（SVM）公式推导

假设一堆训练数据的正负样本标记为 

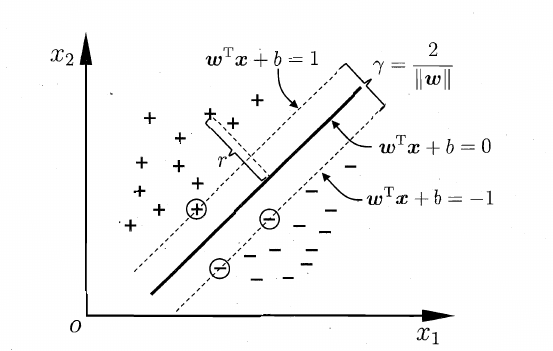
假设有一个超平面H：  ，可以通过此线性方程划分，同时存在两个平行于H的超平面H1和H2：

超平面H能够正确分类，也就是满足如下约束：

即：

            （1）

离H最近的正负样本刚好分别落在H1和H2上使等号成立，它们就是支持向量。

而超平面H1和H2的距离可知为（注：线到线的距离公式求得）：

  

 

SVM目标找到具有“最大间隔”的划分超平面。即找到满足（1）的约束条件的参数w,b，使得r最大。显然，最大化间隔r，也就是最小化。于是可以构造如下的条件极值问题：

                         （2）

这就是基本向量机的基本型。

对于不等式约束的条件极值问题，可以用拉格朗日方法求解。拉格朗日方程的构造规则是：用约束方程乘以非负的拉格朗日系数，然后再从目标函数中减去。得到拉格朗日方程如下：

                                        （3）

其中：

                                                                  （4）

那么处理的规划问题就变为：

                     （5）

上式才是严格的不等式约束的拉格朗日条件极值的表达式。下面将详细地一步步推导。

 （5）式是一个凸优化问题，其意义是先对α求偏导，令其等于0消掉α，然后再对w和b求L的最小值。要直接求解（5）式是有难度的，通过消去拉格朗日系数来化简方程，对我们的问题无济于事。但可以通过拉格朗日对偶问题来解决，为此我们把（5）式做一个等价变换，即为对偶变换：

 

从而凸规划问题转换成了对偶问题：

                                  （6）

 

其意义是：原凸优化问题可以转化为先对w和b求偏导，令其等于0消掉w和b，然后再对α求L的最大值。下面求解（6）式，先计算w和b的偏导数。由（3）式有：

                                                    （7）

 

让L在w和b上取到最小值，令（7）式的两个偏导数分别为0，得到：

                                                     （8）

 

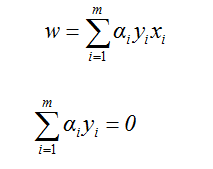
将（8）代回（3）式，可得：

 

                            

                          

                                                                                                               （9）

 再把（9）代入（6）式有：

             （10）

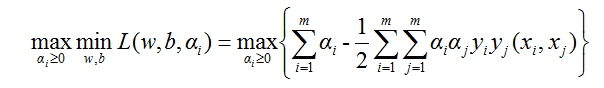
考虑到（8）式，我们的对偶问题就变为：

               （11）

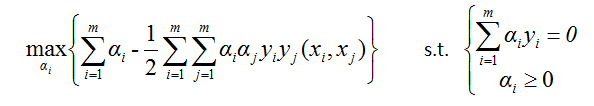
上式这个规划问题可以直接从数值方法计算求解。

 

需要指出的一点是，（2）式的条件极值问题能够转化为（5）式的凸规划问题，其中隐含着一个约束，即：

 （12）

 

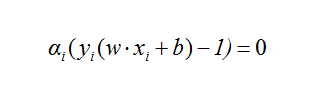
（12）推理：如果（2）和（5）等效，则必有：

                           

 

 

（3）式代入上式中，得到：

 

                         

 

化简得到：

                                            （13）

 

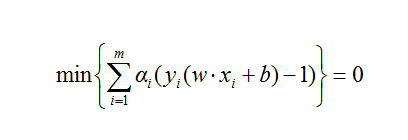
又因为约束（1）式和（4）式，有：

所以要使（13）式成立，只有令：，由此得到（12）式的约束。（12）式的约束的意义是：如果一个样本是支持向量，则其对应的拉格朗日系数非零；如果一个样本不是支持向量，则其对应的拉格朗日系数一定为0。由此可知大多数拉格朗日系数都是0。

其中，式（1）、（4）、（12）即KKT条件。

一旦我们从（11）式求解出所有拉格朗日系数，就可以通过（8）式的

计算得到最优分割面H的法向量w。而分割阈值b也可以通过（12）式的约束用支持向量计算出来。找到最优的H1和H2，即训练出的SVM。

 

机器学习-周志华

http://blog.sina.com.cn/s/blog_4298002e010144k8.html