矩阵幂_快速幂_矩阵乘法_模板

版权声明：点个关注(＾－＾)V https://blog.csdn.net/weixin_41793113/article/details/88431485

最近遇到快速幂的题目有点儿多,写写模板，整理下

【矩阵快速幂】

　　该算法只适用于方阵

　　设 A 为方阵 , 快速求 A n 的算法

【应用】求递推式的第n项，例如

　　斐波那契 递推公式 f(n) = f(n-1)  + f(n-2)

　　可以转换成以下矩阵运算：

　　

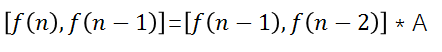
　　由上述递推式我们可以求出矩阵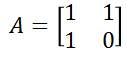

因此原本求 f(1000) 需要递推1000次，时间复杂度为O（n）

用矩阵快速幂，求f(1000, 999) = f(2, 1) * A1000   设方阵阶数为m,矩阵相乘相乘时间复杂度为 O（m3），矩阵快速幂为O（logn）

则计算8*log21000  < 1000 

数论的题目数据规模都很大,一般会让我们取模,有时候变量改成long也是必要的

public class 矩阵幂_快速幂_矩阵乘法_模板 {

	public static void main(String[] args) {
		int[][] a = new int[][] {{1,1,1},{1,1,1},{1,1,1}};
		System.out.println(mpow(2, 4));
		a = mul(a,a);
		for(int i=0;i<a.length;i++) {
			for(int j=0;j<a[0].length;j++) 
				System.out.print(a[i][j]+" ");
			System.out.println();
		}
		a = mpow(a,2);
		for(int i=0;i<a.length;i++) {
			for(int j=0;j<a[0].length;j++) 
				System.out.print(a[i][j]+" ");
			System.out.println();
		}
			

	}
	
	static final int MOD = 1000000007;//数论的题目数据规模都很大,一般会让我们取模,有时候变量改成long也是必要的
//	static int n;//全局变量,数据规模
	

	//快速幂模板1
	static int mpow(int a,int n) {
		int ans = 1;
		while(n>0) {
			if((n&1)==1)//感觉写n%2==1好些
				ans = ans*a%MOD;
			a = (a*a)%MOD;
			n>>=1;
		}
		return ans;
	}
	//快速幂模板2
	static int mpow(int a,int n,int mod) {
		int ans = 1;
		while(n>0) {
			if((n&1)==1)//感觉写n%2==1好些
				ans = ans*a%mod;
			a = (a*a)%mod;
			n>>=1;
		}
		return ans;
	}
	//这里是矩阵的乘法模板，默认方阵
	static int[][] mul(int[][] a,int[][] b){
		int n = a.length;
		int[][] ans = new int[n][n];
		for(int i=0;i<n;i++)
			for(int j=0;j<n;j++)
				for(int k=0;k<n;k++)
					ans[i][j] =(ans[i][j] + a[i][k]*b[k][j])%MOD;//ans[i][j] += a[i][k]*a[k][j];
		return ans;
	}
	//矩阵快速幂_模板
	static int[][] mpow(int[][] a,int n){
		int N = a.length;
		int[][] ans = new int[N][N];
		for(int i=0;i<N;i++)
			ans[i][i] = 1;//初始化为单位矩阵W
		while(n>0) {//写 n!=0也行,会快些么，反正位运算是会快的.这个不清楚
			if((n&1)==1) 
				ans = mul(ans,a);
			a = mul(a,a);
			n>>=1;
		}
		return ans;
	}

}