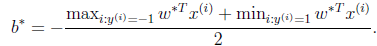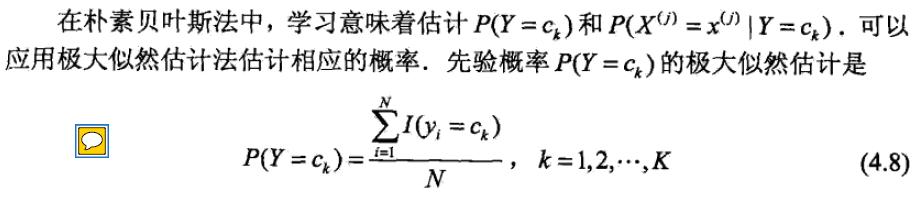机器学习——有监督学习知识积累

线性回归

最小二乘法小结

感知机

感知机原理小结

在《统计学习方法》中，定义的方式有一些不同，如下图所示

书中所提到了“不考虑 $\frac{1}{\|w\|}$”，实际意思是说不会影响解，
对于最小化问题 $-\frac {1} {\|w\|}\sum y_i(wx_i+b)$来说，如果我们添加一个条件 $\|w\|=1$后（注意，添加这个条件之后，并不会对原问题的意义进行改变，仍然是在找经验误差最小的分类面，但加入说要是假设分子为1，那这个优化问题的意义就改变了），优化问题变成了 $-\frac {1} {1}\sum y_i(wx_i+b)$，得到一组解 $w_1=[w_{11},w_{12}...],b_1$；然后把这个条件改成 $\|w\|=2$后，优化问题变成了 $-\frac {1} {2}\sum y_i(wx_i+b)$，得到了第二组解 $w_2=[w_{21},w_{22}...],b_2$，很容易能看出这两个优化问题是完全相同的，并且第一组解和第二组解的对应项的比例是相同的，比如 $\frac{w_{11}}{w_{21}}=\frac{w_{21}}{w_{22}}=\frac{b_{1}}{b_{2}}=\frac{1}{2}$，也就是说不仅两个优化问题的最终大小一样，所代表的的分类面也一样
进而能说明的是，即使不对 $w$进行约束，无论 $w$在优化过程中会怎样变化，最终的解所代表的分类面也都是唯一的，反正最终的最优解中 $\|w\|$都是一个常数 $a$
另外刘建平的博客里有另一种解释方法，即把样本所处的n维特征空间扩充为n+1维，就是把那个常数1也当做特征的一个维度，样本就从 $x=[x_1,x_2,...]$变成了 $x=[1,x_1,x_2,...]$，并且参数空间也从n维扩充到了n+1维，参数就从 $w,b$变成了 $\theta=[b,w]$，于是点到新空间的分类面的距离就变成了 $\frac{\theta x}{\|\theta\|}$，所以无论 $\theta$是多大都不影响最终的解

最近邻

详解KDTree
《机器学习实战》学习笔记——基于sklearn使用 KNN

用balltree找某个目标点target的所属的时候，我猜应该是从上往下依次比较target点距离左球与右球的球心的距离，距离哪个球心更近，就走哪条路径

Logistics

逻辑斯蒂回归（Logistic Regression）

永远记住， $P(y=1|X,w)=\frac{e^{w^Tx}}{1+e^{w^Tx}}$，是因为二分类问题中一般 $f(x)>0$就判定为 $\hat{y}=1$，另外LR二分类模型中，样本类别是{0,1}，其实也可以是别的，只不过这样好定义损失函数。
上面博客有错误，对似然函数最大化应该是梯度上升而不是下降

Softmax回归

SVM

SMO优化算法（Sequential minimal optimization）
支持向量机通俗导论（理解SVM的三层境界）

支持向量机的核心：支持向量机的模型构建意义是找到一个分类超平面，能够把特征空间中的样本全部正确分类的同时，保证距离分类超平面最近的样本能够尽可能远离这个分类超平面，距离的评估用的是几何间隔，也就是高中数学中的点到平面距离，于是就有了如下优化问题（称这个优化问题为问题A），其中 $\hat{r}$就是距离分类超平面最近的样本（支持向量）距离分类平面的函数距离，并且在线性可分的情况下，超平面两侧的支持向量的到超平面的距离相同，都是 $\hat{r}$
$问题A:\max_{w,b} \frac{\hat{r}}{\|w\|},s.t.\ y_i(w^Tx_i+b)\ge\hat{r}$

并且同时，无论这个距离分类超平面最近的样本是样本集中的哪个点、位置在哪，都将这个点到达分类超平面的函数距离设置为1，于是原问题就变成了新的优化问题（称这个优化问题为问题B） $问题B:\max_{w,b} \frac{1}{\|w\|},s.t.\ y_i(w^Tx_i+b)\ge1$

可以从如下两个角度来理解：第一，函数间隔的大小收到点与分类面的相对位置和分类超平面的参数的两方面的影响，一旦支持向量确定，那么更改分类超平面的参数就会等比例的放大或者缩小函数间隔，而这个函数间隔的变化并不会让分类超平面变化。第二，设置距离分类超平面最近的样本到平面的函数间隔为1，其实类似于在设置单位，训练集一旦确定，分类面也一定是确定的
这里我想给出我自己的理解方法，在问题A的基础上人为添加一个条件 $\hat{r}=1$，得到如下优化问题，称之为问题C，很容易知道问题C的解可能不是问题A的解，但这两个问题代表的超平面一定是同一个超平面
$\begin{aligned}问题C:&\max_{w,b} \frac{\hat{r}}{\|w\|}\\ s.t.&\ y_i(w^Tx_i+b)\ge\hat{r}\\ &\hat{r}=1 \end{aligned}$

如果我们现在解开了问题A，得到的解 $w_A^*,b_A^*$，这个解代表了SVM的分类超平面，但这个解并不一定是问题C的解，但如果对 $w_A^*,b_A^*$进行等比例的放大或者缩小得到 $w_C^*,b_C^*$使得 $\hat{r}=1$成立，那么这个 $w_C^*,b_C^*$就是问题C的解，但注意， $w_A^*,b_A^*$与 $w_C^*,b_C^*$代表的平面是同一个平面
而由于问题C相当于在问题B上添加了约束，所以其可行域比问题B更小，所以如果问题C有解，这个解也一定是问题B的解
所以仅仅从分类面的同一性角度来说， $w_B^*,b_B^*$与 $w_A^*,b_A^*$是同一个分类面，问题A与问题B也就等价了，解的具体是多大就无所谓了

文中有下式

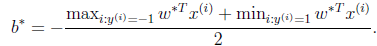
之所以 $b^*$是这个，是因为那两个max和min对应的是分类面两边的支持向量，而且分类面肯定过这两个支持向量的中点
至于为什么非支持向量样本对应的的 $\alpha_i=0$，是因为首先非支持向量不是距离分类面最近的点，所以满足 $y_i(w^Tx_i+b)\gt1$，又因为解要满足KKT条件，即 $\alpha_iy_i(w^Tx_i+b)=0$，所以有如上结论
核函数存在的意义：原本的思路是将低维空间 $x\in R^d$通过函数 $\phi$映射到高维空间 $\phi(x)\in R^{d+m}$，把原本线性不可分的数据变成高维空间的线性可分数据，然后在高维空间求解如下问题，从而计算分类面参数去做SVM
$\max_{w,b} \frac{1}{\|w\|},s.t.\ y_i(w^T\phi(x)+b)\ge1且w\in R^{d+m}$
这有着维度爆炸的问题，那么核函数的出现告诉我们没有必要先映射后在高维空间求解，在低维空间同样可以完成这个事情，为什么呢？因为求解SVM的对偶问题的时候，我们需要的仅仅是训练集中任意两个样本的内积而已，要做的就仅仅是在求解对偶问题的时候，把两个向量的内积变成高维空间下的内积就可以了，而核函数就是一种用来算高维空间内积的函数
SMO的KKT条件可以推出这个KKT条件说明，在两条间隔线外面的点，对应 $\alpha$为0，在两条间隔线里面的对应 $\alpha$为C，在两条间隔线上的样本的 $\alpha$在0和C之间。
求解对偶问题的时候软间隔的约束条件没了，是因为当 $0\le\alpha\le C$隐含了软间隔的约束条件

支持向量机(SVM)的特点与不足

多核学习

从 SVM 到多核学习 MKL
特征提取-特征后期融合-多核学习方法（MKL）

贝叶斯方法

算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)
朴素贝叶斯算法原理小结

贝叶斯决策（后验概率最大化）西瓜书这块讲的好一些
假设可能的样本类标记为 $\{c_1,...,c_N\}$，而 $\lambda_{ij}$是将真实标记为 $c_j$的样本分类为 $c_i$的损失，样本 $x$来自于后验分布 $P(c_k|x)$，如何求将一个已知的样本 $x$被分类为 $c_i$时的误差呢？
假设这个样本 $x$的类是 $c_1$，那么将其分类为 $c_i$的误差为 $\lambda_{i1}$，发生这样的事情的概率是 $P(c_1|x)$
假设这个样本 $x$的类是 $c_2$，那么将其分类为 $c_i$的误差为 $\lambda_{i2}$，发生这样的事情的概率是 $P(c_2|x)$
可以看到“将一个已知的样本 $x$被分类为 $c_i$时的误差”是一个随机变量，那么这个随机变量的期望是多少呢？很简单， $R(c_i|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_j|x)$，这个就是在样本 $x$上预测的期望损失或条件风险。
进一步，假设我们现在手上有一个判定器 $h$，它把样本 $x$判定为 $h(x)$类，那么 $h(x)$的在全部数据损失的期望或总体风险就是 $R(h)=\mathbb{E}_x[R(h(x)|x)]$。要最小化它，每个 $R(h(x)|x)$都是最小的就可以了。直白的说，只要判定器 $h$对于给定的样本 $x$做出的决策，可以使得 $R(h(x)|x)$尽可能小就行。如果损失是0-1损失，那么 $h(x)=argmax_{c}P(c|x)$就满足要求了，就是说决策器每次的输出都是 $P(c|x)$最大时的那个c就可以了。
朴素贝叶斯是怎么用贝叶斯决策的了呢？因为 $P(c_i|x)$事先是未知的，所以朴素贝叶斯要先去学习 $P(c_i|x)$，然后做的事就一样了

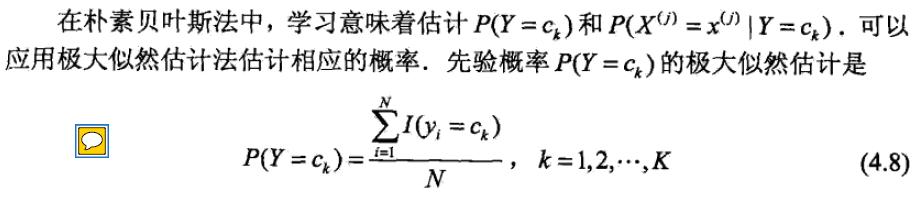
说来生气，之前和组里的老师和同学讨论这个问题的时候，我说这个值是极大似然估计出来的，他们说极大什么极大，这不就明摆着的么，呵呵= =
这个式子实在太通俗易懂了，所以没人追究他是怎么来的，这个式子讲的是：我们一共有 $N$个样本，其中 $c_k$类的样本有 $a$个，那么随机采样出现 $c_k$的概率就是 $\frac{a}{N}$
设从样本集中随机采样一个样本是 $c_k$类的概率为 $\theta$，设采样 $N$次结果中出现了 $a$个 $c_k$类的事件为 $A$，那么似然函数为 $L(\theta)=P(A|\theta)=C_N^a\theta^a(1-\theta)^{N-a}$于是对似然函数求导为 $\frac{\partial L}{\partial \theta}=C_N^a\theta^{a-1}(1-\theta)^{N-a-1}[a(1-\theta)-(N-a)\theta]$，等于0时，刚好有 $\theta=\frac{a}{N}$

从贝叶斯方法谈到贝叶斯网络

决策树

决策树算法原理(上)

为什么信息增益倾向于选择多的特征，直观来讲，选特征数目多的，输出的叶子节点会更纯，可以让每个叶子节点更纯
假设数据中的每个人都是一个样本，每个人的姓名都不同，那么信息增益就会选择姓名作为最佳属性，因为按姓名分裂后，每个叶子节点只包含一条记录，而每个叶子只属于一类（信息增益最大），因此纯度最高。但是这样的分类没有意义。
举个实际数据例子，假如一个两类问题之中，总样本数目为4，其中正样本数目为2，负样本数目为2，并且该样本有 $a,b$两个特征，其中特征 $a$的取值可以是 $a_1,a_2$，总样本之中，特征 $a,b$当取不同值的，样本分布情况如下表，如：特征 $a$取值为 $a_1$的样本数目为2，其中正负样本数目均为1。
可以算出总样本的熵 $H(D)=-\frac{1}{2}*log\frac{1}{2}-\frac{1}{2}*log\frac{1}{2}$
当特征选a的时候， $H(D|a)=-\frac{2}{4}(\frac{1}{2}*log\frac{1}{2}+\frac{1}{2}*log\frac{1}{2})-\frac{2}{4}(\frac{1}{2}*log\frac{1}{2}+\frac{1}{2}*log\frac{1}{2})$
当特征选b的时候， $H(D|b)=-\frac{1}{4}*log\frac{1}{1}-\frac{1}{4}*log\frac{1}{1}-\frac{1}{4}*log\frac{1}{1}-\frac{1}{4}*log\frac{1}{1}$
所以 $[H(D)-H(D|b)]>[H(D)-H(D|a)]$，但此时选择特征取值更多的特征是因为b特征好，而不是因为多才选他的，“倾向选择取值更多的特征”不一定就是坏事，因为熵和分类误差率的单调性完全一致，因此即使有着“倾向选择取值更多的特征”的性质，也不会使得一个不好的特征的信息增益比一个好的特征高；但仍不能否认，仅从数据的角度来看b特征就是比a特征好。甚至把问题再深入一点，假设下面表格中样本数目都乘以一百万，数据量足够大的时候b特征仍能保持一个特别好分类结果，那么也就证明了b特征就是一个很好的特征。

特征a取值	样本数目	正样本数目	负样本数目
$a_1$	2	1	1
$a_2$	2	1	1

特征b取值	样本数目	正样本数目	负样本数目
$b_1$	1	1	0
$b_2$	1	0	1
$b_3$	1	1	0
$b_4$	1	0	1

信息熵是描述数据的混乱程度的，公式为 $H(X) = -\sum\limits_{i=1}^{n}p_i logp_i$，既然是混乱程度，那就要有一个关注的角度，比如现在把世界上所有的哺乳动物都抓进来作为我们的数据，我们现在从物种的角度看这个数据，那这个数据乱的不得了，熵也一定特别高；但如果我们现在关注的是是不是胎生的，那这批数据纯的不得了，因为全是胎生的，熵为0。
回到机器学习，对于数据 $D$来说，其关于类别的混乱程度为 $H_{class}(D) = -\sum\limits_{k=1}^{K}\frac{|D_k|}{|D|}log_2\frac{|D_k|}{|D|}$，其中 $D_k$为 $D$中类别为 $k$的样本集；其关于特征 $A$的混乱程度为 $H_A(D) = -\sum\limits_{i=1}^{V}\frac{|D^{i}|}{|D|}log_2\frac{|D^{i}|}{|D|}$，其中 $D^{i}$为 $D$中特征 $A$取值为 $a_i$的样本集； $H_A(D)$就是信息增 益率的分母，一般来说，特征 $A$取值越多， $H_A(D)$会越大，因为数据 $D$里的样本在特征值 $A$取各个值的都有，那就说明从 $A$特征的角度，这个数据乱嘛

c4.5为什么使用信息增益比来选择特征？ - 夕小瑶的回答 - 知乎

正经解释了信息增益率的特点，“样本数越少，对概率的估计结果的方差就会越大”这段话的需要解释一下：比如估计投一枚均匀的硬币得到正面的概率，每次实验只投4次，每次都用频率估计概率，做1000次实验，那么每次实验得到的结果，放在一起，方差一定特别大；而如果修改为每次实验投10000次，那么这些结果的方差一定很小。进一步地，如果我们只取一次实验结果作为最终实验结果，只投4次得到的结果有很大概率是不贴近0.5的（也就是说结果有偏向），而投10000次得到的结果很大概率贴近0.5（结果没有偏向）。
而体现到机器学习的特征选择上，如果某个特征的可选择的值多，如果把这个特征作为分支，如果那么每个分支的样本数目较少，由上面的理论，样本在该特征上的样本类别分布有较大可能性是有偏的，以两类问题为例，如果在特征 $A$上取值为 $a_i$样本的类别的真实的分布是5:5，如果我们只有10个样本，两类样本多一个少一个会对熵造成很大影响，不同类别的样本比例是4:6至6:4的概率只有0.65625。但如果我们有100个样本呢，样本比例是40:60到60:40之间的概率高达0.9648。于是由于这10个样本上，不同类别的样本比例在4:6至6:4之外的概率更高，因此计算的信息熵更有可能会比真实的小一些，这全是因为我们样本太少了。数据集的不充足以及客观存在的大数定律导致取值多的特征在计算条件熵时容易估计出偏小的条件熵。
信息增益为什么会偏向于特征值多的特征？基于上面的道理再往前想一步，如果现在样本数目一定，特征 $A$可取的特征值多，那以特征 $A$进行将样本划分开，得到的多个样本集都会较小，小会发生什么？数据不充足，不充足会发生啥？这个样本集的条件熵偏小，偏小怎么了？信息增益就大了呗。

决策树算法原理(下)

$GINI(D,A)=min_{v\in\{1,..,V\}}\frac{|D^v|}{|D|}GINI(D^v)+\frac{|D-D^v|}{|D|}GINI(D-D^v)$

scikit-learn决策树算法类库使用小结

集成学习

集成学习原理小结
Bagging与随机森林算法原理小结
集成学习之Adaboost算法原理小结

统计学习方法中146页的解释

由8.4式可知，每一次迭代后每个样本权值变化公式为
$\begin{aligned} w_{m+1,i}&=\frac{w_{m,i}}{Z_m}exp(-\alpha_m y_i G_m(x_i))\\ &=\frac{w_{m-1,i}}{Z_{m-1}Z_m}exp(-\alpha_{m-1} y_{i} G_{m-1}(x_{i}))exp(-\alpha_m y_i G_m(x_i))\\ &=\frac{w_{1,i}}{\prod_{k=1}^m{Z_k}}exp(\sum_{k=1}^m-\alpha_{k} y_{i} G_{k}(x_{i}))\\ &=\frac{1}{N\prod_{k=1}^m{Z_k}}exp(\sum_{k=1}^m-\alpha_{k} y_{i} G_{k}(x_{i})) \end{aligned}$
并且 $f_{m-1}(x)=\sum_{k=1}^{m-1}\alpha_kG_k(x)$，所以有
$w_{m,i}=\frac{1}{N\prod_{k=1}^{m-1}{Z_k}}exp(-y_i f_{m-1}(x))=\frac{1}{N\prod_{k=1}^{m-1}{Z_k}}\bar{w}_{m,i}$
并且由于 $Z_k$对任意样本都相同，并且 $\alpha>0$是一个恒定值，当 $\sum_{i=1}^{n}\bar{w}_{mi}I(y_i\ne G(x_i))$最小的时候，8.21同时最小，因此说 $G_m^*$就是AdaBoost算法之中第m轮输出的基本分类器，

梯度提升树(GBDT)原理小结

GBDT相对于BDT（提升树）好在哪呢，为什么一定要用负梯度来拟合呢？
如果我们用的是平方损失，那么在训练新树的时候，就要针对 $L(y,f_{m-1}(x)+T(x;\theta_m))=[y-f_{m-1}(x)-T(x;\theta_m)]^2=[r-T(x;\theta_m)]^2$这时候新的树恰好需要拟合残差而已，但如果这个损失是个别的损失，那新树要去拟合的就不是残差了；而实际上可以把 $L$看做以 $f$为自变量的函数，于是对 $L$关于 $f$进行梯度下降得到 $\frac{\partial L}{\partial f}$，也就是说当自变量 $f$沿着负梯度方向的时候， $L$减小最快，那么在实际数据中要做的就是学习一个新模型，使得当输入为 $x$时输出值为 $\frac{\partial L}{\partial f}$，把这个模型加回给之前的模型，就完成了对 $L$的梯度下降工作
在GBDT回归的时候，每一个新的弱分类器的叶子节点个数可能都不一样，GBDT回归的核心之一在于每个叶子节点的值的选择
多元GBDT分类的每个 $f_k(x)$代表的是针对“是第k类样本”和“不是第k类样本”的分类模型

GBDT处理二分类问题

这篇文章把GBDT处理分类问题时候讲的明白了一些，说白了就是把损失函数换成 $L(y,F)=log(1+exp(-2yF)),y \epsilon -1,1$，然后把 $F(x)=\frac{1}{2}log[\frac{Pr(y=1|x)}{Pr(y=-1|x)}]$，反过来看就是 $Pr(y=1|x)= \frac{1}{1+e^{-2F(x)}}$，把 $F(x)$映射成了区间位于0到1的概率
这里我是这样理解的，首先对于原始样本 $D$训练一个二分类树 $T_{pre}$，然后GBDT中的第一棵树并不是 $T_{pre}$，而是 $T_1(x)=\frac{1}{2}log[\frac{Pr(y=1|x)}{Pr(y=-1|x)}]$，其中概率是由 $T_{pre}$输出的。然后求梯度，下一次就按着回归的方法生成回归树 ${T_2,...,T_m}$了。然后把树加起来的输出就是 $F(x)=\frac{1}{2}log[\frac{Pr(y=1|x)}{Pr(y=-1|x)}]$

一步一步理解GB、GBDT、xgboost
机器学习教程 之 梯度提升方法：GBDT及其扩展模型XGBoost

找分割点的时候，类似于CART树的CCP过程，比较某个叶子节点继续分裂好还是不分裂好，而且只看这一个节点的就行了；感觉只在特征选取的时候用了GINI，其他时候如分割点和叶子结点的确定，都是新的方法

Complete Guide to Parameter Tuning in XGBoost (with codes in Python)

综合

感知机、线性回归、逻辑回归的简单对比