计算机视觉中的多视图几何——第一章:2D摄影几何（2.相似变换、仿射变换、射影变换）

版权声明：本文为博主原创文章， 欢迎转载，转载请注明出处。 https://blog.csdn.net/baicaidiaozhui/article/details/86534023

1.3射影变换

• 射影映射（几何定义）： 是 $IP^2$到它自身的一种满足下列条件的可逆映射 $h$：三点 $x_1、x_2、x_3$共线当且仅当 $h(x_1)、h(x_2)、h(x_3)$也共线；射影映射也称为保线变换、射影变换、单应。

• 映射 $h$ (代数定义)： $IP^2 \rightarrow IP^2$是射影映射的充要条件：存在一个 $3 \times 3$的非奇异矩阵 $H$,使得 $IP^2$的任何一个用矢量 $\bm{x}$ 表示的点都满足 $h(x)=H\bm{x}$

• 任何射影映射都是以这种齐次坐标线性变换的方式出现
• 任何这样的变换都是射影映射，证明如下：
  令 $\bm{x_1,x_2,x_3}$都在同一直线 $\bm{I}$上，因此， $\bm{I}^T\bm{x_i}=0,i=1,2,3$.令 $H为3\times3$非奇异矩阵。可以证明 $\bm{I}^THH^T\bm{x_i}=0$；
  因此点 $Hx_i$都在直线 $\bm{I}^TH$上，即该变换具有保线性。

• 射影变换 平面射影变换是一种关于齐次3维矢量的线性变换，并可以一种非奇异的 $3\times3$矩阵 $H$来表示：

$\begin{bmatrix} x_1' \\ x_2'\\ x_3' \end{bmatrix}= \begin{bmatrix} h_11&h_12&h_13\\ h_21&h_22&h_23\\ h_31&h_32&h_33 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}$
简洁表示为： $\bm{x}'=H\bm{x}$;
其中矩阵 $H$乘以任何一个不为零的比率因子射影射影变换都不会发生改变，即 $H$是一个齐次矩阵。 $H$矩阵中有9个未知量，但与点的齐次表示一样，有意义的仅仅是矩阵元素之间的比率关系，在矩阵 $H$中有八个独立的比率，因此一个射影变换有八个自由度。

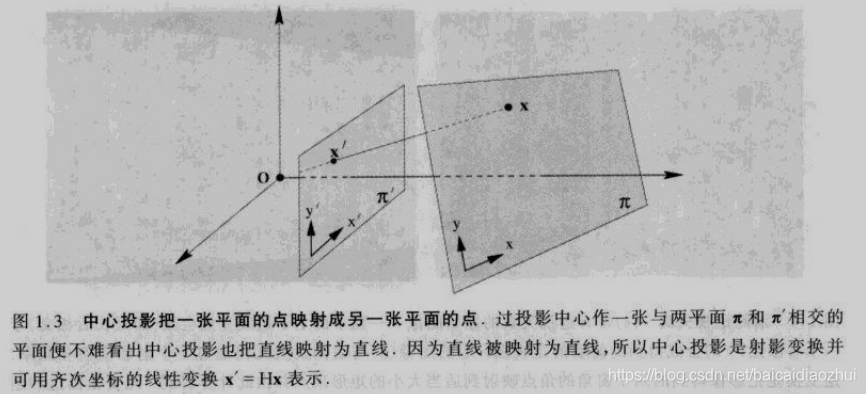
• 平面之间的映射
  中心投影映射将一张平面上的点映射到另一张平面的点。如果每一张平面上建立坐标系并采用齐次坐标来表示点，那么中心投影映射可以表示成为 $\bm{x}'=H\bm{x}$,其中 $H$为 $3\times3$的非奇异矩阵。
  
• 直线变换

在点变换 $\bm{x_i}'=H\bm{x_i}$下，直线变换为
$\bm{I}^T=H^{-T}\bm{I}$

• 二次曲线变换

在点变换 $\bm{x_i}'=H\bm{x_i}$下，二次曲线 $C$变换为:
$C'=H^{-T}CH^{-1}$
对偶二次曲线C变换为:
$C^{*'}=HC^*H^T$

1.4 变换的层次

$n\times n$可逆是矩阵的群称为一般线性群 $GL(n)$。当把非零纯量因子的矩阵都视为等同时，便得到射影线性群 ，记 $PL(n)$为 $GL(n)$的商群，在平面射影变换时n=3。
$PL(n)$中最重要的子群就是仿射群和欧式群，仿射群是有最后一行为(0,0,1)的矩阵组成的子群；而欧式群是仿射群的子群其左上角的 $2\times 2$矩阵的行列式值是正交的。当左上角的 $2\times 2$矩阵的行列式值为1时，为定向欧式群。

1.等距变换

• 等距变换是平面 $IR^2$的变换，它保持欧式距离不变。一个等距变换可以表示为：
  $\begin {pmatrix} x'\\ y'\\ 1 \end {pmatrix}= \begin{bmatrix} \varepsilon \cos \theta & - \sin\theta & t_x \\ \varepsilon \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$
  其中 $\varepsilon=\pm1$.当 $\varepsilon =1$ 那么该等距变换是保向的并且是旋转、平移的复合欧式变换 。如果 $\varepsilon =-1$,那么该等距变换是逆向的。欧式变换是刚体运动的模型。
  平面欧式变换的简介形式：
  $\bm{x'}=H_E\bm{x}= \begin{bmatrix} \bm{R}&\bm{t}\\ \bm{0^T}&\bm{1} \end{bmatrix}\bm{x}$
  其中 $R是2\times 2$旋转矩阵(满足 $RR^T=R^TR=I的$正交矩阵),t为二维平移矢量，0是二维零矢量。当 $\bm{t=0}$时为纯旋转，当 $\bm{R=I}$时为纯平移。

• 不变量 长度、夹角、面积；
• 群和定向 保向的等距变换形成一个群，但逆向的不是。
• 平面欧式变换有三个自由度，可由两组点对算出（一组点对可得到两个方程）

2.相似变换

• 相似变换是等距变换和均匀缩放的复合，矩阵表示如下：
  $\begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} s\cos\theta&-s\sin\theta&t_x\\ s\sin\theta&s\cos\theta&t_y\\ 0&0&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$
  分块简介形式
  $\bm{x}'=H_S\bm{x}= \begin{bmatrix} s\bm{R}&\bm{t}\\ \bm{0^T}&\bm{1} \end{bmatrix}\bm{x}$
  其中s表示均匀缩放。相似变换也叫等形变换，形状保持不变。

• 不变量： 夹角、两直线长度的比率、两面积的比率
• 度量结构： 确定到只相差一个相似变换的结构
• 相似变换有四个自由度，比欧式变换多一个缩放自由度，相似变换可由两组点对算出（一组点对可得到两个方程）。

3.仿射变换

• 相似变换是非奇异变换和平移变换的复合，矩阵表示如下：
  $\begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} a_{11}&a_{12}&t_x\\ a_{21}&a_{22}&t_y\\ 0&0&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$
  分块简介形式
  $\bm{x}'=H_A\bm{x}= \begin{bmatrix} \bm{A}&\bm{t}\\ \bm{0}&\bm{1} \end{bmatrix}\bm{x}$
  其中A为 $2\times 2$的非奇异矩阵。
• A线性变换矩阵可以看做两个基本变换——旋转和非均匀缩放的复合，仿射矩阵A总能分解为：
  $A=R(\theta)R(-\phi)DR(\phi)$
  其中 $R(\theta)和R(\phi)$分别表示 $\theta和\phi$的旋转矩阵，而D为对角矩阵：
  $\bm{D}=\begin{bmatrix} \lambda_1&0\\ 0&\lambda_2 \end{bmatrix}$
  利用 $SVD$分解推导如下： $A=UDV^T =UV^T(VDV^T)=R(\theta)R(-\phi)DR(\phi)$；SVD分解所得的 $U、V$均为正交矩阵。因此仿射矩阵A分解如下：

• 先利用正交矩阵 $V_T$矩阵进行一个 $(\phi)$角度旋转；
• 再利用对角矩阵D对旋转后的x和y方向分别进行按比例因此 $\lambda_1和\lambda_2$进行缩放；
• 再利用 $V$矩阵进行 $\phi$角度的回转；
• 最后，再利用 $UV^T$矩阵对经以上特定方向拉伸之后的矩阵进行 $(\theta)$角度的旋转；注解：其中容易得出 $\theta=\theta_u+\theta_v$;

仿射变换矩阵比相似变换矩阵多两个自由度，缩放方向的角度 $\phi$和缩放参数比率 $\lambda_1:\lambda_2$。仿射变换的（形变）本质是在特定角度的两个垂直方向上进行缩放。

不变量：

• 平行线；
• 平行线段的长度比：
• 面积比

仿射变换有六个自由度，可由三组点对算出。

4.射影变换

如1.3所述，射影变换是齐次坐标的一般非奇异线性变换。分块的形式如下：
$\bm{x}'=H_p\bm{x}= \begin{bmatrix} \bm{A}&\bm{t}\\ \bm{v}^T&v \end{bmatrix}\bm{x}$

变换矩阵中有九个元素，但只有它们的比率才有意义，因此该变换矩阵中需要确认8个参数。两平面之间的射影变换可由四个点对计算获得。但其中属于同一平面内的三个点必须不共线
不变量 : 射影变换中四共线点的“”交比保持不变，即线段比率的比率保持不变。

5.射影变换和仿射变换的区别

仿射变换是相似变换的推广，射影变换是仿射变换的推广。

仿射变换： 对平面的变换作用是均匀的，对于确定的仿射变换，平面上任何地方的面积变换的缩放因子是一致的；直线变换的方向与直线所处平面位置无关，而是取决于原来的方向。
透视变换： 对于给定的透视变换，面积的缩放随位置的改变而改变，直线变换的方向既和原方向相关也和所处位置相关。

射影变换和仿射变换的根本区别在于射影变换中矢量 $\bm{v}$不为零。对理想点 $(x_1,x_2,0)^T$分别进行仿射变换和射影变换如下：
仿射变换

$\begin{bmatrix} \bm{A}&\bm{t}\\ \bm{0}^T&\bm{1} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix}= \begin{bmatrix} \bm{A}\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\\ 0 \end{bmatrix}$
仿射变换后理想点依然为理想点在无穷远处；

射影变换

$\begin{bmatrix} \bm{A}&\bm{t}\\ \bm{v}^T&\bm{1} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix}= \begin{bmatrix} \bm{A}\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\\ v_1x_1+v_2x_2 \end{bmatrix}$
**射影变换之后理想点被映射为有限点。**鉴于此射影变换能够对消影点进行建模。

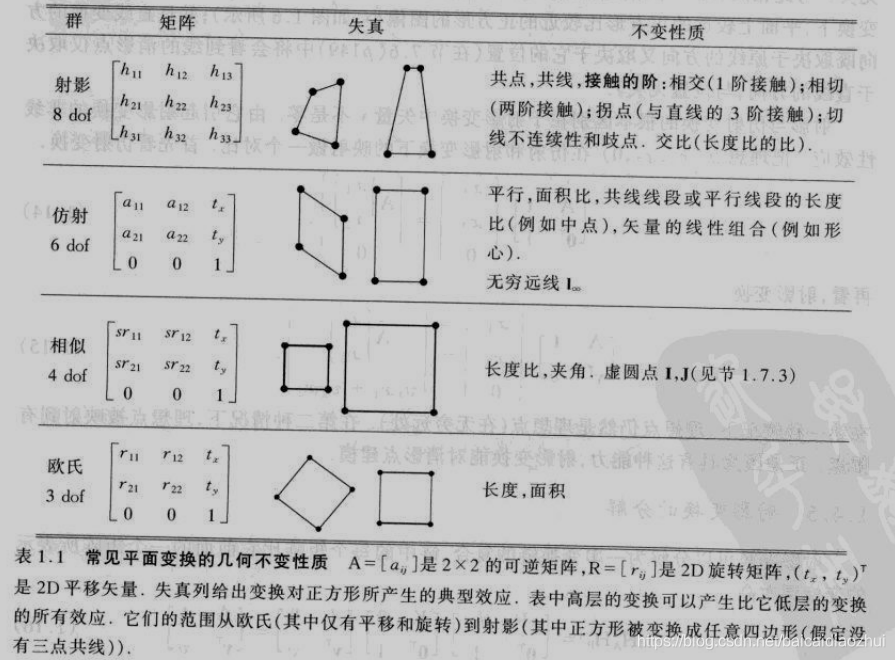
6.不变量的数目

与函数无关的不变量数等于或大于配置的自由度数减去变换的自由度数。

参考文献：

1、计算机视觉中的多视图几何。