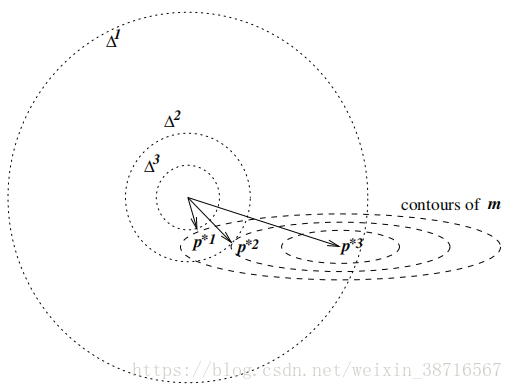
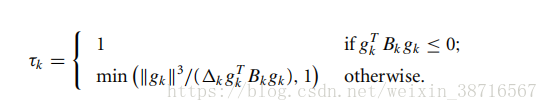TR方法比LS方法收敛速度快

TR方法中有几个参数需要选择：

模型函数 $m_{k}$
信赖域 $\Delta _{k}$
求解参数 $p_{k}$

$\mathbf{m_{k}}$

when $\alpha =1$ ，Taylor-series expansion of f around $x_{k}$ ，which is

$f(x_{k}+p)=f({x_{k}})+\bigtriangledown f(x_{k})p+\frac{1}{2}p^{T}\bigtriangledown ^{2}f(x+tp)p$

where t is some scalar in the interval (0,1).

By using an approximation $B_{k}$ to the Hessian in the second-order term:

$m_{k}(p)=f_{k}+g_{k}^{T}p+\frac{1}{2}p^{T}B_{k}p$

Then we seek a solution of subproblem:

${\color{Blue} min } m_{k}(p)=f_{k}+g_{k}^{T}p+\frac{1}{2}p^{T}B_{k}p$

$s.t. \left \| p \right \| <\bigtriangleup _{k}$

The difference between $m_{k}(p)$ and $f(x_{k}+p)$ is $O(\left \| p \right \|^{2})$ , which is small when p is small.

$\mathbf{\bigtriangleup _{k}}$

Let

$\rho _{k}=\frac{f(x_{k})-f(x_{k}+p_{k})}{m_{k}(0)-m_{k}(p_{k})}$

1.if $\rho _{k}$ is negative , the newe value $f_{k+1}$ is greater than $f_{k}$ , so the step must be rejected.,because step $p_{k}}$ is obtained by minimizing the model $m_{k}$ .

2.if $\rho _{k}$ is close to 1, so it safe to expand the trust region.

3.if $\rho _{k}$ is postive but significantly smaller than 1,we do not alter the trust region.

4.if $\rho _{k}$ is close to 0, we shrink the trust region.

专注于求解子问题：

We sometimes drop the interation subscript k and restate the problem as follows:

${\color{Cyan} min} m(p)=f+g^{T}p+\frac{1}{2}p^{T}Bp$

$s.t. \left \| p \right \|\leq \bigtriangleup$

if and only if

(4.8b) is a complementarity condition that states at least one of $\lambda$ and ( $\bigtriangleup -\left \| p^{*} \right \|$ ) must be 0.

When $\bigtriangleup =\bigtriangleup _{1}$ ， $p^{*3}$ lies strictly inside the trust region，we must have $\lambda =0$ .

When $\bigtriangleup =\bigtriangleup _{2}$ or $\bigtriangleup _{3}$ , we have $\bigtriangleup -\left \| p^{*} \right \|=0$ , then we get

$\lambda p^{*}=-Bp^{*}-g=-\bigtriangledown m(p^{*})$

Finally we get p.

4.1 Algotithms based on the Cauchy Point

Find an approximate solution

4.1.1 The Cauchy Point

1.Find the vector $p_{k}^{s}$ by solving a linear version of subproblem,that is,

$p_{k}^{s}={\color{Cyan} arg}min f_{k}+g_{k}^{T}p$ $s.t. \left \| p \right \|\leq \bigtriangleup _{k}$

2.Calculate the scalar $\tau _{k}$

$\tau _{k}={\color{Cyan} arg}min m_{k}(\tau p_{k}^{s})$ $s.t. \left \| \tau p_{k}^{s} \right \|\leq \bigtriangleup _{k}$

3.Set $p_{k}^{c}=\tau _{k}p_{k}^{s}$ .

When $g_{k}^{T}B_{k}g_{k}\leq 0$ , $m_{k}$ decreases monotonically with $\tau$ , so $\tau =1$

When $g_{k}^{T}B_{k}g_{k}> 0$ , min $m_{k}$ ,so $\tau =\frac{\left \| g_{k} \right \|^{3}}{\bigtriangleup _{k}g_{k}^{T}B_{k}g_{k}}$

$p_{k}^{s}=-\frac{\bigtriangleup _{k}}{\left \| g_{k} \right \|}g_{k}$
$m_{k}(\tau p_{k}^{s})=f_{k}+\tau p_{k}^{s}\bigtriangledown f_{k}^{T}+\frac{1}{2}\tau ^{2}(p_{k}^{s})B_{k}p_{k}^{s}$

Taking the Cauchy point as our step,we are simply implementing the steepest descent method with a particular choice if step length.

4.1.2 The Dogleg Method

It can be used when B is positive definite.

${\color{Cyan} min} m(p)=f+g^{T}p+\frac{1}{2}p^{T}Bp$ $s.t. \left \| p \right \|\leq \bigtriangleup$

We denote the solution of it by $p^{*}(\bigtriangleup )$ .

When $\left \| p^{B} \right \|=\left \| -B^{-1} g\right \|\leq \bigtriangleup$ , $p^{*}(\bigtriangleup )=p^{B}$
When $\left \| p^{B} \right \|=\left \| -B^{-1} g\right \|>\bigtriangleup$ , then we have the restriction $\left \| p \right \|\leq \bigtriangleup$ ,so

$m(p)\approx f+g^{T}p$

so, $p\approx -\frac{g_{k}}{\left \| g_{k} \right \|}$ .

Consider the step length $\alpha$ . $\alpha =-\frac{g^{T}g}{g^{T}Bg}$ ,then we have

${\color{Red} p^{U}=-\frac{g^{T}g}{g^{T}Bg}g}$

1.When $p^{U}=\bigtriangleup$ , then we choose $p^{U}$

2..When $p^{U}>\bigtriangleup$ , then let $\left \| \tau p^{U} \right \|=\bigtriangleup$ , we choose $\tau p^{U}$

3..When $p^{U}<\bigtriangleup$ , then we want $p^{U}$ be close to $p^{B}$ , so

$p^{*}(\bigtriangleup )=\begin{cases} \tau p^{U} & \text{ if } 0\leq \tau \leq 1 \\ p^{U}+(\tau -1)(p^{B}-p^{U})& \text{ if } 1\leq\tau \leq 2 \end{cases}$

where

$\begin{cases} \tau =\frac{\bigtriangleup _{k}}{p^{U}} \in [0,1]\\ \tau \in \left \| p^{U}+(\tau -1)(p^{B}-p^{U})=\bigtriangleup _{K} \right \|\in [1,2] \end{cases}$

4.1.3 Two-Dimensional subspace minimization

The dogleg method for p can be widen to the entire two-dimensional subspace spanned by pU and pB (equivalently, g and $-B^{-1}g$ ). The subproblem is replaced by

${\color{Cyan} min }m(p)=f+g^{T}p+\frac{1}{2}p^{T}Bp\qquad s.t.\,\left \| p \right \|<\bigtriangleup ,\,p\in span[g,\,B^{-1}g].$

【Numberical Optimization】4 Trust-Region Methods (zen学习笔记)

专注于求解子问题：