吴恩达机器学习笔记（五）——逻辑回归

前言

前面几章我们学习了线性和非线性回归问题的解决方法，下面我们来学习分类问题。图像识别、语言识别、垃圾邮件过滤等技术归根结底都是属于分类问题。我们先从最简单的二分类问题开始学习。

一、 问题介绍

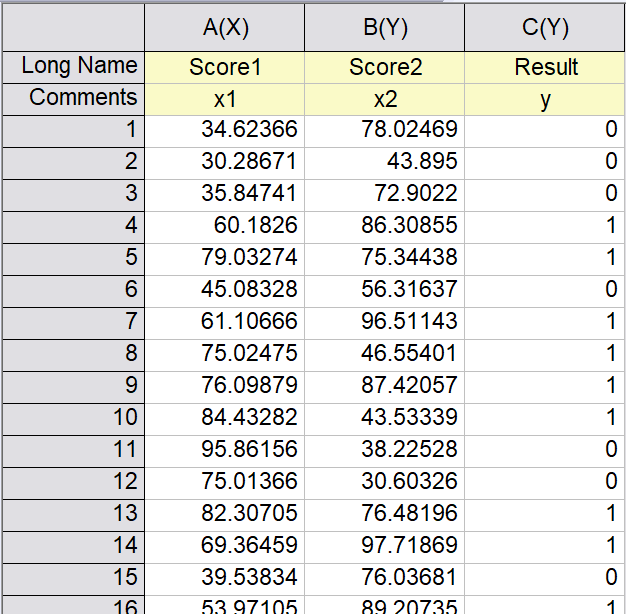
我们仍然通过一个例子来学习逻辑回归算法。我们这次要解决的问题是通过考试分数预测学生能否被录取。假设某所学校，会根据两门考试的成绩来决定是否录取该学生，现在已知100名学生的考试成绩和录取结果，需要找出录取结果与考试成绩的关系。
　　我们将问题抽象出来：我们有两个特征 $x_1,x_2$分别代表两门考试的成绩，用 $y$来代表录取的结果，由于结果只有录取和不录取两种情况，因此 $y$只有两种取值，我们令这两个值分别为0和1，0代表没录取，1代表录取。我们的训练集如下图所示：
　　　　
将这些数据画出来，如下图所示：
　　　　
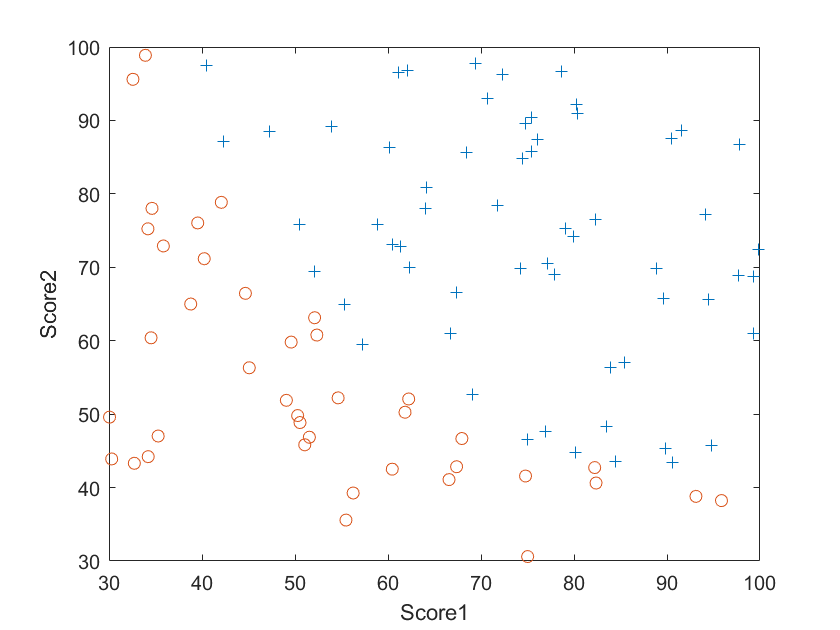
图中蓝色的“+”代表录取，红色的“o”代表未被录取，我们的任务就是找出录取的数据和未被录取的数据之间的分解线，从而对任意成绩预测其能否被录取。观察我们的数据，可以发现其分界线大致为一条直线，可以用 $0=\theta_0+\theta_1x_1+\theta_2x_2$来表示，而不需要引入 $x_1^2、x_2^2$等高次项。

二、Sigmoid函数

需要注意的是，由于 $y$变成了离散的0和1，我们不能再使用回归问题中使用的方法来处理。我们需要定义一个新的假设函数来拟合离散的 $y$值，这个新的假设函数表达式为：
　　　　 $h_\theta(x)=g(\mathbf{\theta}^T\mathbf{x}), 　g(z)=\frac{1}{1+e^{-z}}$
其中，函数 $g$就是Sigmoid函数，其特殊之处在于 $z$与 $g$之间有如下对应关系：

$z$	$g(z)$
0	0.5
>>0	1
<<0	0

我们规定，输入特征 $\mathbf{x}$对应的输出为 $y=\left \{\begin{array}{}1,&h_\mathbf{\theta}(x)≥0.5\\0,&h_\mathbf{\theta}(x)<0.5\end{array}\right.$，根据Sigmoid函数的性质，有 $y=\left \{\begin{array}{}1,&\mathbf{\theta}^T\mathbf{x}≥0\\0,&\mathbf{\theta}^T\mathbf{x}<0\end{array}\right.$。于是， $\mathbf{\theta}^T\mathbf{x}=0$就是所有的正样本和负样本之间的分界线。
　　至此，通过引入Sigmoid函数，和定义其与输出标签之前的对应关系，我们将离散函数转变为连续的函数。接下来，我们就可以按照以前的路线来解决我们的问题了：定义代价函数、计算代价函数的偏导数、使用梯度下降算法寻找最优参数。

三、代价函数

根据刚才的分析，我们接下来就是要定义代价函数了。我们先来看刚才定义的假设函数： $h_\theta(x)=g(\mathbf{\theta}^T\mathbf{x})$，我们也可以将其理解为预测的输出值为1的概率： $h_\theta(x)=1$就意味着我们预测的输出结果百分之百为1， $h_\theta(x)=0$就意味着我们预测输出结果不可能为1，而是百分之百为0。
　　现在，我们的目标是优化参数 $\mathbf{\theta}$使得我们的预测值尽可能地与训练集符合。也就是说，对于任意一个样本 $(\mathbf{x}^{(i)},y^{(i)})$，如果我们的预测值 $h_\theta(\mathbf{x}^{(i)})=0$而实际上 $y^{(i)}=1$，或者我们的预测值 $h_\theta(\mathbf{x}^{(i)})=1$而实际上 $y^{(i)}=0$，都说明我们估算得很差，这个时候的代价函数都应该很大。而如果我们的预测 $h_\theta(\mathbf{x}^{(i)})=1$，实际上确实 $y^{(i)}=1$或者我们的预测 $h_\theta(\mathbf{x}^{(i)})=0$而实际上确实 $y^{(i)}=0$，就说明我们的预测很准确，这个时候的代价函数就应该很小。
　　根据以上原则，人们定义的代价函数为：
　　 $J=-\frac{1}{m}\sum\limits_{i=1}^{m}{[y^{(i)}logh_\mathbf{\theta}(\mathbf{x}^{(i)})+(1-y^{(i)})log(1-h_\mathbf{\theta}(\mathbf{x}^{(i)}))]}$
使用Matlab画出代价函数的函数曲线，如下图所示：
　　　　
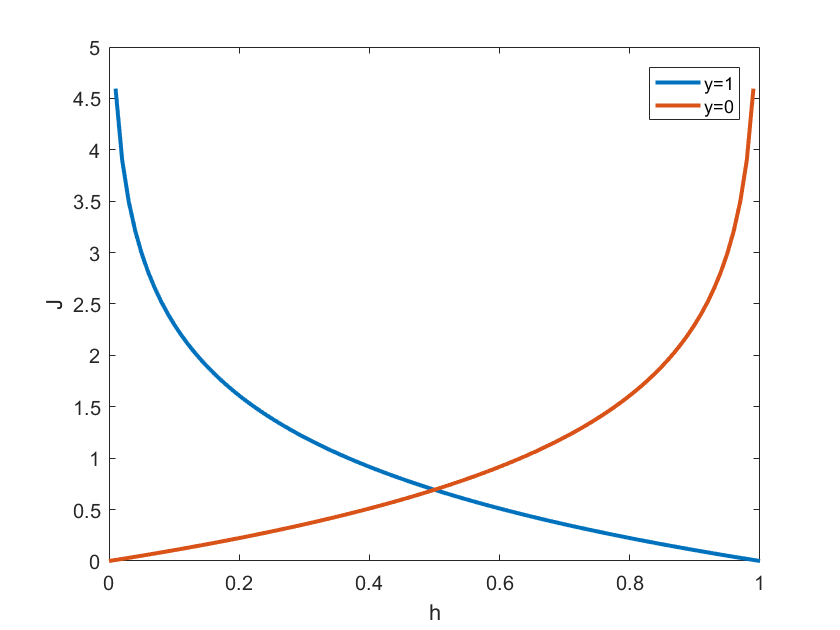
对每一个样本，它的实际输出值只能是0或1，因此其代价函数只能是红色或蓝色中的一条曲线。对于实际输出值为0的样本，代价函数为红色曲线， $h=0$时，代价函数最小，且随着 $h$增加而指数增加；反过来，对于实际输出值为1的样本，其代价函数为蓝色曲线， $h=1$时，代价函数最小，且随着 $h$减小而指数增加。因此，只要我们将代价函数优化到最小值，就能保证预测值与训练集符合的最好。

四、梯度下降

接下来的任务就是计算出代价函数对参数 $\mathbf{\theta}$的偏导数，并将其应用到梯度下降算法中去。我们将假设函数的表达式： $h_\mathbf{\theta}(\mathbf{x}=\frac{1}{1+e^{\mathbf{\theta}^T\mathbf{x}}})$代入代价函数的表达式中，然后运用链式法则就可以求出：
　　 $\frac{\partial{J}}{\partial{\mathbf{\theta}}}=-\frac{1}{m}\sum\limits_{i=1}^{m}{[h_{\mathbf{\theta}}(\mathbf{x}^{(i)})-y^{(i)}]\mathbf{x}^{(i)}}$
其中， $\mathbf{\theta}=\left[\begin{matrix}\theta_0\\\theta_1\\\theta_2\end{matrix}\right]$， $\mathbf {x}=\left[\begin{matrix} 1\\x_1\\x_2\end{matrix}\right]$。巧妙的是，这里的偏导数与线性回归问题中的偏导数的表达式完全相同，只是假设函数的表达式不一样而已。
　　得到了代价函数的梯度表达式以后，就可以运用梯度下降算法来寻找最优参数了。逻辑回归中梯度下降算法与线性回归中的方法一样：
　　　　Step1、初始化 $\mathbf{\theta}$：例如令 $\theta_{0}=\theta_{1}=\theta_{2}=\cdots=0$;
　　　　Step2、计算当前 $\mathbf{\theta}$值对应的 $J$的梯度值： $\frac{\partial{J}}{\partial{\theta_{0}}}$， $\frac{\partial{J}}{\partial{\theta_{1}}}$， $\frac{\partial{J}}{\partial{\theta_{2}}}$ $\cdots$；
　　　　Step3、更新 $\mathbf{\theta}$： $\theta_{0}:=\theta_{0}-\alpha*\frac{\partial{J}}{\partial{\theta_{0}}}$； $\theta_{1}:=\theta_{1}-\alpha*\frac{\partial{J}}{\partial{\theta_{1}}}$; $\theta_{2}:=\theta_{2}-\alpha*\frac{\partial{J}}{\partial{\theta_{2}}}$; $\cdots$
　　　　Step4、判断是否结束循环，若为否则回到Step2。

五、Matlab代码实现

弄清楚逻辑回归算法的具体原理和流程后，我们就可以使用Matlab来编写代码解决我们这章最开始提的问题啦。具体的代码如下所示：

close all;
clear all;
clc;
%Load and draw out the test samples
samples=load('ex2\ex2data1.txt');
x=samples(:,1:2);
y=samples(:,3);
pos=find(y==1);
neg=find(y==0);
figure(1),
plot(x(pos,1),x(pos,2),'+');
hold on;
plot(x(neg,1),x(neg,2),'o');
xlabel('Score1');
ylabel('Score2');


m=length(y);
x=[ones(m,1),x];

%Normalize the x data in test samples. x must be normalized, otherwise the 
%function may convergence to a sudo-local-minimum point, which depend on
%the initial theta sensitively.
xn1=x(:,2);
xn2=x(:,3);
xn1=(xn1-mean(xn1))/std(xn1);
xn2=(xn2-mean(xn2))/std(xn2);
xn=[ones(m,1),xn1,xn2];

%Initialize the parameters and minimize J with gradient descent function.
theta=zeros(3,1);
alpha=20;
figure,
for step=1:30
    [J,grad]=CostFunction(theta,xn,y);
    theta=theta-alpha*grad;
    plot(step,log10(J),'o');
    xlabel('Step');
    ylabel('log(J)');
    drawnow;
    hold on;
end

%Recover theta for x before normalization.
xn1=x(:,2);
xn2=x(:,3);
theta(1)=theta(1)-theta(2)*mean(xn1)/std(xn1)-theta(3)*mean(xn2)/std(xn2);
theta(2)=theta(2)/std(xn1);
theta(3)=theta(3)/std(xn2);

%Draw out the fitting result.
x1=30:1:100;
x2=(-theta(1)-theta(2)*x1)/theta(3);
figure(1)
plot(x1,x2,'linewidth',2);
drawnow;

function [J,grad]=CostFunction(theta,X,y)
m=length(y);
J = 0;
grad = zeros(size(theta));
h=Sigmoid(X*theta);
J=-1/m*(y'*log(h)+(1-y)'*log(1-h));
grad=1/m*(X'*(h-y));

function y=Sigmoid(x)
y=1./(1+exp(-x));
end

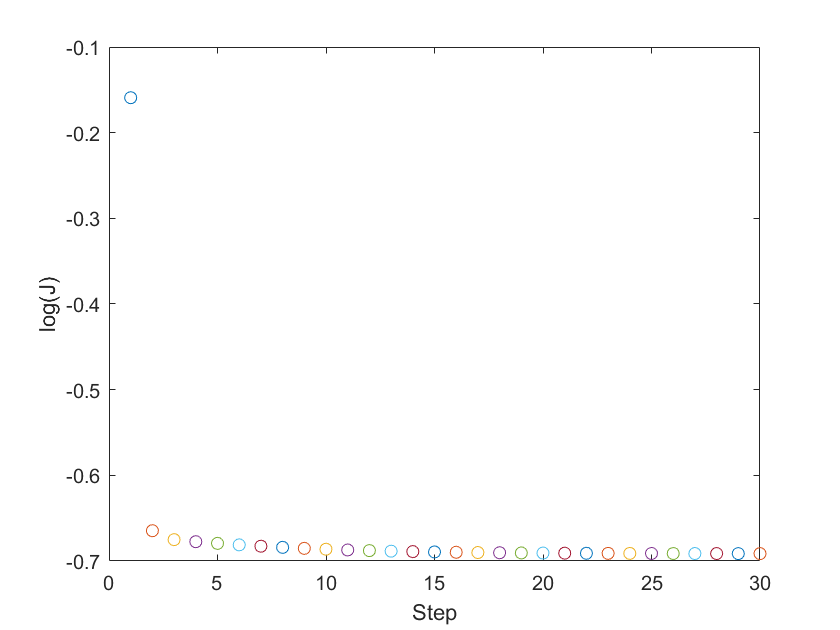
程序的运行结果如下：
　　　　
　　　　
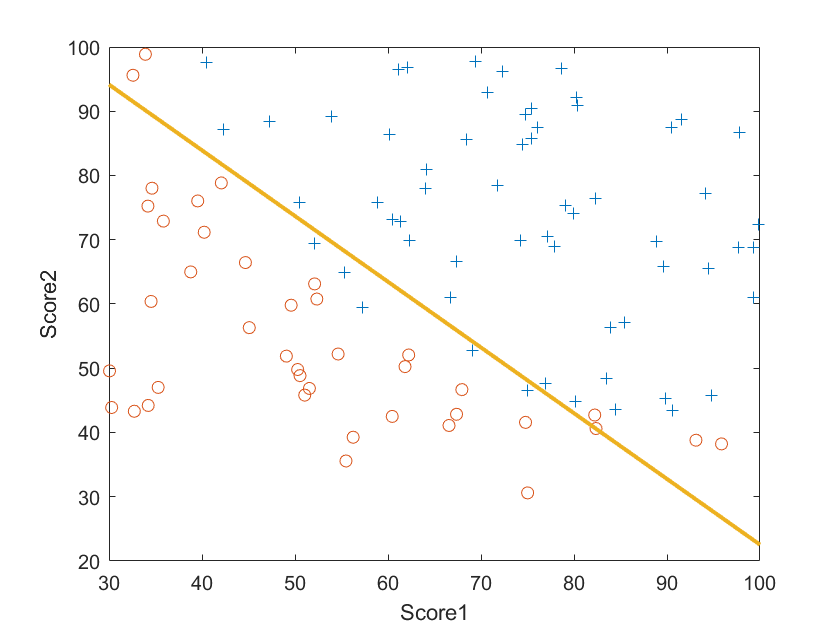
以上程序和数据可以从这里下载，提取码ea14

六、结语

这一章介绍了逻辑回归算法的原理和实现过程。由于我们这里使用的例子的分界线比较简单，我们使用直线的形式就可以达到要求。然而，大部分情况下，正负样本的分界线会是一个复杂的曲线或曲面，这个时候，就会涉及到过拟合和欠拟合的问题，我们需要使用正则化的方法来防止出现过拟合，这些就是我们下一章的内容。