定义

向量(列向量)：仅含一列的矩阵称为列向量，或简称向量。

知识点

$\large \mathbb{R}^{2}$ 中的向量

所有两个元素的向量的集记为 $\mathbb{R}^{2}$ ， $\mathbb{R}$ 表示向量中的元素是实数，而指数2表示每个向量包含两个元素。

$\mathbb{R}^{2}$ 中两个向量相等当且仅当其对应元素相等。 $\left[ \begin{matrix} 4 \\ 7 \end{matrix} \right ]$ 和 $\left[ \begin{matrix} 7 \\ 4 \end{matrix} \right ]$ 是不相等的，因为 $\mathbb{R}^{2}$ 中的向量是实数的有序对。

给定 $\mathbb{R}^{2}$ 中两个向量u和v，它们的和u+v是把u和v对应元素相加所得的向量。

给定向量u和实数c，u和c的标量乘法(或数乘)是把u的每个元素乘以c，所得向量记为cu。

案例

给定u= $\left[ \begin{matrix} 1 \\ -2 \end{matix} \right ]$ ，v= $\left[ \begin{matrix} 2 \\ -5 \end{matix} \right ]$ 。求4u，(-3)v以及4u+(-3)v。

解：4u= $\left[ \begin{matrix} 4 \\ -8 \end{matrix} \right ]$ ，(-3)v= $\left[ \begin{matrix} -6 \\ 15 \end{matrix} \right ]$ ，4u+(-3)v= $\left[ \begin{matrix} 4 \\ -8 \end{matrix} \right ]$ + $\left[ \begin{matrix} -6 \\ 15 \end{matrix} \right ]$ = $\left[ \begin{matrix} -2\\ 7 \end{matrix} \right ]$

$\large \mathbb{R}^{2}$ 的几何表示

因为平面上每个点有实数的有序对确定，所以可把几何点(a,b)与列向量 $\large \left[ \begin{matrix} a\\b \end{matrix} \right ]$ 等同。因此可把 $\mathbb{R}^{2}$ 看作平面上所有点的集合。

向量 $\large \left[ \begin{matrix} a\\b \end{matrix} \right ]$ 的几何表示是一条由原点(a, b)指向点(a, b)的有向线段。

两个向量的和也有很有用的几何意义。下面规则可用解析几何的知识证明。

向量加法的平行四边形法则

若 $\mathbb{R}^{2}$ 中向量u和v用平面上的点表示，则u+v对应于以u，0和v为3个顶点的平行四边形的第4个顶点。

平行四边形法则

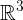$\large \mathbb{R}^{3}$ 中的向量

$\mathbb{R}^{3}$ 中的向量是 $3\times1$ 列矩阵，有3个元素。它们表示三维坐标空间中的点，或起点为原点的箭头。

$\large \mathbb{R}^{n}$ 中的向量

若n是正整数，则 $\mathbb{R}^{n}$ 表示所有n个实数数列(或有序n元组)的集合，通常写成 $n\times1$ 列矩阵的形式。如：u= $\left[ \begin{matrix} u_1\\ u_2\\ \cdots\\ u_n \end{matrix} \right ]$

所有元素都是零的向量称为零向量，用0表示(0中元素的个数可由上下文确定)。

$\mathbb{R}^{n}$ 中向量的代数性质：

对 $\mathbb{R}^{n}$ 中一切向量u，v，w以及标量c和d：

u+v=v+u
(u+v)+w=u+(v+w)
u+0=0+u=u
u+(-u)=-u+u=0
c(u+v)=cu+cv
(c+d)u=cu+du
c(du)=(cd)u
1u=u

线性组合

给定 $\mathbb{R}^{n}$ 中向量 $\boldsymbol{v_1,v_2,\cdots,v_p}$ 和标量 $c_1,c_2,\cdots,c_p$ ，向量 $\boldsymbol{y}=c_1\boldsymbol{v_1}+\cdots+c_p\boldsymbol{v_p}$ ，称为向量 $\boldsymbol{v_1,v_2,\cdots,v_p}$ 以 $c_1,c_2,\cdots,c_p$ 为权的线性组合。

设 $\boldsymbol{a_1}$ = $\left[ \begin{matrix} 1\\ -2\\ -5 \end{matrix} \right ]$ ， $\boldsymbol{a_2}$ = $\left[ \begin{matrix} 2\\ 5\\ 6 \end{matrix} \right ]$ ， $\boldsymbol{b}$ = $\left[ \begin{matrix} 7\\ 4\\ -3 \end{matrix} \right ]$ ，确定 $\boldsymbol{b}$ 能否写成 $\boldsymbol{a_1}$ 和 $\boldsymbol{a_2}$ 的线性组合，也就是说，确定是否存在权 $x_1$ 和 $x_2$ 使 $x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}=\boldsymbol{b}$ 。若向量方程有解，求它的解。

解：根据向量加法和标量乘法的定义，把向量方程 $x_1 \left[\begin{matrix} 1 \\ -2 \\ -5 \end{matrix}\right ] + x_2 \left[\begin{matrix} 2 \\ 5 \\ 6 \end{matrix}\right ] = \left[\begin{matrix} 7 \\ 4 \\ -3 \end{matrix}\right ]$ 写成 $\left[\begin{matrix} x_1 \\ -2x_1 \\ -5x_1 \end{matrix}\right ] + \left[\begin{matrix} 2x_2 \\ 5x_2 \\ 6x_2 \end{matrix}\right ] = \left[\begin{matrix} 7 \\ 4 \\ -3 \end{matrix}\right ]$ 或 $\left[\begin{matrix} x_1 +2x_2 \\ -2x_1+5x_2 \\ -5x_1+6x_2\end{matrix}\right ] = \left[\begin{matrix} 7 \\ 4 \\ -3 \end{matrix}\right ]$ 。左右两边的向量相等当且仅当它们的对应元素相等。即 $x_1$ 和 $x_2$ 满足向量方程当且仅当 $x_1$ 和 $x_2$ 满足线性方程组 $\begin{cases} x_1+2x_2=7 \\ -2x_1+5x_2=4 \\ -5x_1+6x_2=-3 \end{cases}$ 。用行化简算法将线性方程组的增广矩阵化简，以此解方程组。

$\left[ \begin{matrix} 1 & 2 & 7 \\ -2 & 5 & 4 \\ -5 & 6 & -3 \end{matrix} \right ]$ ~ $\left[ \begin{matrix} 1 & 2 & 7 \\ 0 & 9 & 18 \\ 0 & 16 & 32 \end{matrix} \right ]$ ~ $\left[ \begin{matrix} 1 & 2 & 7 \\ 0 & 1 & 2 \\ 0 & 16 & 32 \end{matrix} \right ]$ ~ $\left[ \begin{matrix} 1 & 2 & 7 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{matrix} \right ]$ 。方程组的解是 $x_1$ =3， $x_2$ =2。因此 $\boldsymbol{b}$ 是 $\boldsymbol{a_1}$ 与 $\boldsymbol{a_2}$ 的线性组合，权为 $x_1$ =3和 $x_2$ =2。

注意：向量 $\boldsymbol{a_1}$ ， $\boldsymbol{a_2}$ 和 $\boldsymbol{b}$ 是我们进行行化简的增广矩阵的列。这样，向量方程可以直接写出增广矩阵，不必经过一系列步骤。

向量方程 $x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+\cdots+x_n\boldsymbol{a_n}=\boldsymbol{b}$ 和增广矩阵为 $\left[ \begin{matrix} \boldsymbol{a_1} & \boldsymbol{a_2} &\cdots & \boldsymbol{a_n}&\boldsymbol{b} \end{matrix} \right ]$ 的线性方程组有相同的解集。特别地， $\boldsymbol{b}$ 可表示为 $\boldsymbol{a_1},\boldsymbol{a_2},\cdots,\boldsymbol{a_n}$ 的线性组合当且仅当线性方程组有解。

若 $\boldsymbol{v_1,v_2,\cdots,v_p}$ 是 $\mathbb{R}^{n}$ 中的向量，则 $\boldsymbol{v_1,v_2,\cdots,v_p}$ 的所有线性组合所成的集合用记号 $Span \lbrace \boldsymbol{v_1},\boldsymbol{v_2},\cdots,\boldsymbol{v_p} \rbrace$ 表示，称为由 $\boldsymbol{v_1,v_2,\cdots,v_p}$ 所生成(或张成)的 $\mathbb{R}^{n}$ 的子集。也就是说， $Span \lbrace \boldsymbol{v_1},\boldsymbol{v_2},\cdots,\boldsymbol{v_p} \rbrace$ 是所有形如 $c_1\boldsymbol{v_1}+c_2\boldsymbol{v_2}+\cdots+c_p\boldsymbol{v_p}$ 的向量的集合，其中 $c_1,c_2,\cdots,c_p$ 为标量。

要判断向量 $\boldsymbol{b}$ 是否属于 $Span \lbrace \boldsymbol{v_1},\boldsymbol{v_2},\cdots,\boldsymbol{v_p} \rbrace$ ，就是判断向量方程 $c_1\boldsymbol{v_1}+c_2\boldsymbol{v_2}+\cdots+c_p\boldsymbol{v_p}=\boldsymbol{b}$ 是否有解，或等价地，判断增广矩阵为 $\left[ \begin{matrix} \boldsymbol{v_1} & \boldsymbol{v_2} &\cdots & \boldsymbol{v_p}&\boldsymbol{b} \end{matrix} \right ]$ 的线性方程组是否有解。

$\boldsymbol{Span \lbrace v \rbrace}$ 与 $\boldsymbol{Span \lbrace u,v \rbrace}$ 的几何解释

设 $\boldsymbol{v}$ 是 $\mathbb{R}^{3}$ 中的向量，那么 $Span \lbrace \boldsymbol{v} \rbrace$ 就是 $\boldsymbol{v}$ 的所有标量倍数的结合，也就是 $\mathbb{R}^{3}$ 中通过 $\boldsymbol{v}$ 和 $\boldsymbol{0}$ 的直线上所有点的集合。

若 $\boldsymbol{u}$ 和 $\boldsymbol{v}$ 是 $\mathbb{R}^{3}$ 中的非零向量， $\boldsymbol{v}$ 不是 $\boldsymbol{u}$ 的倍数，则 $\boldsymbol{ Span \lbrace u,v \rbrace }$ 是 $\mathbb{R}^{3}$ 中包含 $\boldsymbol{u}$ ， $\boldsymbol{v}$ 和 $\boldsymbol{0}$ 的平面。

向量方程

定义

知识点

中的向量

的几何表示

中的向量

中的向量

线性组合

与的几何解释

猜你喜欢

$\large \mathbb{R}^{2}$ 中的向量

$\large \mathbb{R}^{2}$ 的几何表示

$\large \mathbb{R}^{3}$ 中的向量

$\large \mathbb{R}^{n}$ 中的向量

$\boldsymbol{Span \lbrace v \rbrace}$ 与 $\boldsymbol{Span \lbrace u,v \rbrace}$ 的几何解释