吴恩达机器学习笔记——分类问题

是对应网易云课程吴恩达机器学习第七章的笔记。

分类问题的引入

待预测目标为离散，可以是二分类、多分类问题。如 $y\in \left \{ 0,1 \right \}$ ，其中0表示没有命中目标（负类），1表示命中目标（正类）。（非严格要求）
可以使用：

线性回归拟合：设置分类器输出的阀值，如，横坐标对应的纵坐标高于0.5输出1，否则输出0。适用于正负样本在横轴上集中为两组的情况。算法的输出值可能远大于1或远小于0，具有数据集相关的偶然性，不是一个好的方法，不推荐。
Logistic回归：是一种好用的分类算法，用于y的标签值为0或1的情况下。输出介于0和1之间（包含0和1）。

Logistic回归

logistic函数（sigmoid函数） $h_{\Theta }(x)$

$h_{\Theta }(x)= g(\Theta ^{T}x)$

$g(z)=1/1+e^{-z}$

$h_{\Theta }(x)$ 是输出值代表给定 $\Theta$ 和x的情况下，本算法判断出的结果为1的概率。

决策界限

可以假设 $h_{\Theta }(x)$ >=0.5时，预测结果y=1，此时 $\Theta ^{T}x$ >=0。否则为0。
假设 $\Theta ^{T}x=-3+x1+x2$ ，则决策边界是 $x1+x2=3$ 这条直线。决策边界是假设函数 $h^{_{\Theta }}(x)$ 的属性。一旦确定了 $\Theta$ 参数，就可以完全准确的确定，不需要绘制数据集。数据集用于拟合 $\Theta$ 。
x中可以是x0~xn的任意组合。

拟合Logistic回归——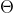 $\Theta$ 参数的自动选择

原来线性回归时设置的代价函数 $J(\Theta )$ 画出的图像有很多局部最优，使用梯度下降可能不易找到全局最优，故我们希望代价函数是一个凸函数。
凸函数Cost函数初始设置

简化后的cost函数：将初始设置的cost函数的分类情况合并为一个式子，并带入代价函数 $J(\Theta )=cost/m$ 。
参数自动选择的算法过程：

将简化后的Cost函数带入代价函数 $J(\Theta )=cost/m$ 。
现欲找到s.t. $J(\Theta )$ 最小的 $\Theta$ （ $\Theta$ 是一个向量），调用梯度下降算法对每一个 $\Theta$ 分量同时更新（代价函数已经被优化为凸函数），直到算法找到全局最优。注：虽然梯度下降算法中 $\Theta _{j}$ 的公式表面上和线性回归时使用的梯度下降一致，实际上带入后截然不同。 $\Theta _{j}$ 的公式中的假设函数 $h_{\Theta }(x^{(i)})$ 在线性回归中是 $\Theta ^{T}x$ ，而在Logistic回归算法中是 $h_{\Theta }(x)= g(\Theta ^{T}x)$ 。
理论上，随着梯度下降算法的运行，调整学习率使得 $J(\Theta )$ 随着运行次数的增加而减小。我们可以画图佐证，如发现异常则采取参数的调整等检查措施。

高级优化

本章介绍的高级优化算法取代梯度下降后可以大大提高Logistic回归算法的运行效率，更适用于多特征、大数据量的机器学习。
三种高级算法：

BFGS
L-BFGS
Conjugate gradient

它们的优点：

通常不需要手动选择学习率 $\alpha$ （内部智能循环，只需要你给定代价函数和计算导数的代码，就可以智能尝试学习率，甚至为每一次循环设置不同的学习率），收敛速度快于梯度下降。

缺点是算法比较复杂，不建议手动编写。可以调用Octave自带的库（有很多参数，比如 $\Theta$ 预估值等）。在Octave里面 $\Theta_0$ 实际上写成theta(1)，因为Octave里向量是从1开始编号的。也即，你需要得到一个能返回代价函数值和梯度值的函数，你需要实现代价函数的计算方法代码和梯度值（每一个分量）的实现代码。

多元分类——一对多

设法转换为多个二元分类问题，如y=1\2\3，设法转化为三个二元分类问题，拟合三个逻辑回归分类器，分别将每一个class作为1，其他class设置为0。这样得到的分类器可以输出三种情况下，待识别对象被判断为正类别的概率。
我们得到结果的原则是，比较所有的 $h_{\Theta }^{(i)}(x)$ ,找到max对应的i，而 $h_{\Theta }^{(i)}(x)$ 就是识别为该类别的概率。