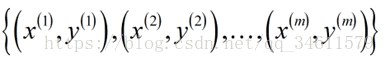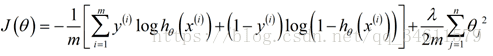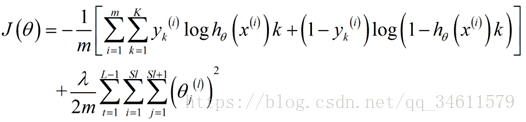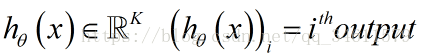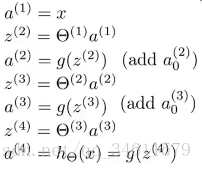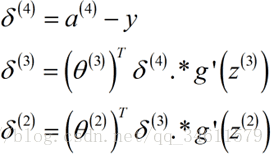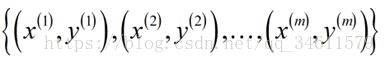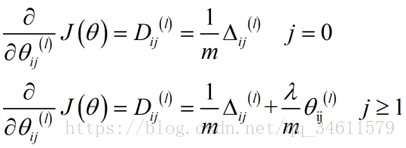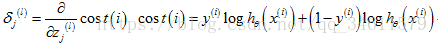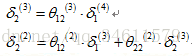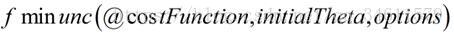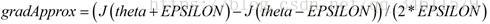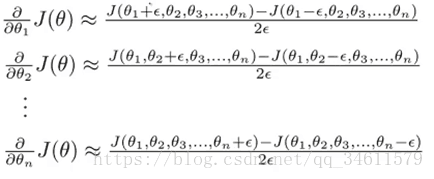第十章 神经网络参数的反向传播算法
代价函数
重点讲解神经网络在分类问题中的应用。
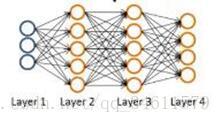
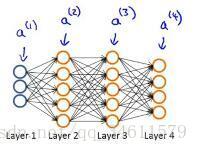
假设有如下的神经网络和训练集:
下面第一种是二元分类问题,第二种是多类别分类问题:
为神经网路定义代价函数,即使用的是逻辑回归中代价函数:
在神经网络来中,这里不再仅有一个逻辑回归输出单元,取而代之的是K个,所以应用到神经网络中的代价函数如下:
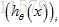
反向传播算法
这一节中主要介绍让代价函数最小化的算法。
使用梯度下降法求解代价函数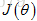
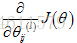
先给出一个样本(x, y)时的正向传播过程:
这里实现了把前向传播向量化,使得可以计算神经网络结构里每个神经元的激活值。
为了计算导数项,采用一种叫做反向传播的算法,反向传播这个名称源于我们从输出层开始计算δ项,然后返回上一层计算隐藏层的δ项,继续往前计算,类似把输出层的误差反向传播给上一层,这就是反向传播。
设置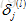
如何实现反向传播算法?
训练集:
①设置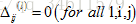
②
遍历训练集,先使用正向传播算法计算出激活值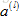
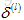
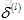
③最后加上正则化项
理解反向传播
为了更好地理解反向传播,首先进一步研究反向传播的过程。
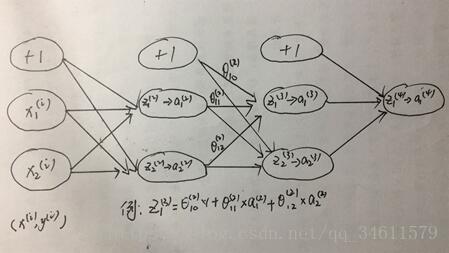
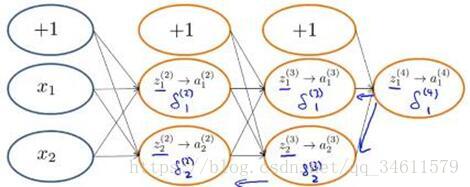
下面是正向传播的过程:
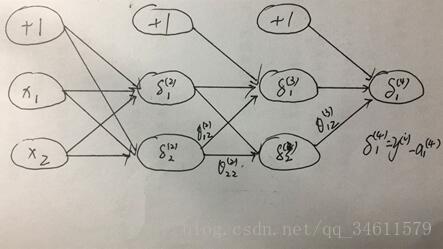
下面是反向传播的过程:
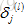
正式的说:
看一下如何计算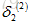
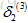
通过以上的图解过程,可以对反向传播有一个更直观的理解。
使用注意:展开参数
这一节将介绍一个细节的实现过程:怎样把参数从矩阵展开成向量,以便于在高级最优化步骤中的使用。
在上面的函数中,我们需要传递的参数为向量。
而事实上,在我们的神经网络中可以发现θ和梯度都为矩阵形式,所以我们需要把矩阵换为向量传递,在函数中将向量转换为矩阵使用。
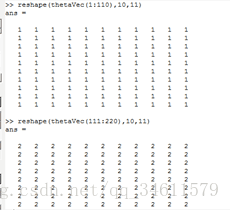
下面举一个例子:
实现过程:
应用于学习算法中:
假设有一些初始参数值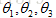
另外一件事是实现待见函数costFunction:
通过对上述内容的学习,我对怎样进行参数的矩阵表达式和向量表达式之间的来回转换有了更清晰的认识。使用矩阵表达式的好处,当你的参数以矩阵的形式存储时,进行正向传播和反向传播时,会觉得更加方便;当你将参数存储存为矩阵时,也更容易充分利用。向量化实现相反地,向量表达式的优点是:如果你有像thetaVec或者DVec这样的矩阵,当使用一些高级的优化算法时,这些算法通常要求把所有的参数要展开成一个长向量的形式。
梯度检测
下面给出一个梯度检测的例子:
(1)梯度的数值估计
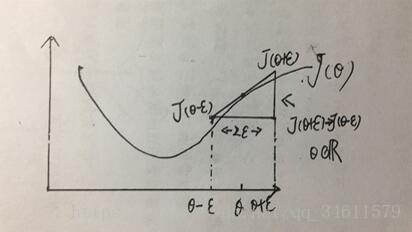
由导数的几何意义如下:
该点导数的计算公式:
考虑到θ是向量的情况,有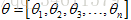
为了估算导数的实现过程:
在神经网络中,使用这种方法时,使用for循环完成对神经网络中代价函数的所有偏导数的计算,与在反向传播中得到梯度进行比较: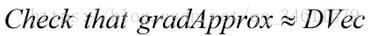
总结:(1)通过反向传播来计算DVec(可能是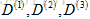
(2)实现数值上的梯度检验计算出gradApprox;
(3)确保DVec和gradApprox都能得到相似的值;
(4)用反向传播代码进行学习的时候要关掉梯度检验。
注意:在运行算法之前(比如多次迭代的梯度下降或是多次迭代训练分类器高级优化算法),要确保禁用梯度检验代码。如果在每次梯度下降迭代或者每次代价函数的内循环里都运行一次梯度检验,程序会变得非常慢。(因为梯度检验比反向传播算法要慢得多)
随机初始化
当调用梯度下降法或者高级的优化算法时,需要为θ赋上一个初始值,想一想,我们能和逻辑回归中那样给初始值设为全0吗?
不行,根据正向传播算法,如果初始值都一样,则每层的单元值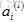
同样,根据反向传播算法,每个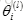
所以每次更新后,这些隐藏单元的每个参数的输入都是相等的,意味着即使梯度下降进行了一次迭代,它们还是以相同的函数作为输入计算。
所以为了解决这样的问题,在神经网络中对参数进行初始化时要使用随机初始化的思想:
初始化的范围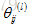
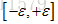
组合
在进行神经网络的训练时,首先就是选择神经网络的结构(神经网络之间的连接模式),
接着是对输入单元和输出单元的选择,然后是对隐藏元单元个数和隐藏层的数目的选择(两种:一个隐藏层;大于一个隐藏层,但每一层的隐藏单元个数一样)。
训练神经网络的实现步骤:
(1) 构建一个神经网络,然后随机初始化权重(通常很小,接近于0);
(2) 执行前向传播算法,即对神经网络输入任意一个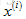
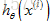
(3) 通过代码计算出代价函数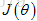
(4) 执行反向传播算法来算出这些偏导数项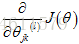
(5) 使用梯度检验来比较这些已经计算得到的偏导数项,把用反向传播算法得到的偏导数值与用数值方法得到的估计值进行比较,
确保两种方法得到相近的值,接下来最重要的一点是停用梯度检验;
(6) 使用一个最优化算法(梯度下降算法或高级优化算法:LBFGS算法、共轭梯度法或其他内置到fminunc函数中的方法),
将这些方法和反向传播算法相结合去最小化代价函数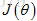
注:神经网络中的代价函数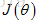
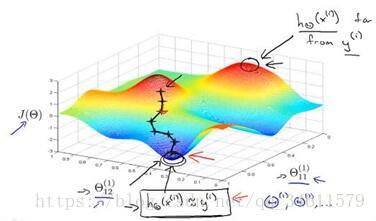
梯度下降法在神经网络中的应用的直观理解:
神经网络的学习和反向传播算法是一个复杂的过程,在学习的过程中有不理解的地方也没有关系,可以继续学习之后的课程,
在实现算法的过程中在仔细的复习,神经网络学习的例子:自动驾驶。