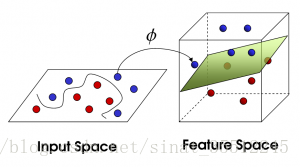
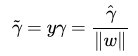机器学习算法（4）——SVM

以一个故事开始SVM方法的学习：

在很久以前的情人节，博瑟要去救他的爱人，但魔鬼和他玩了一个游戏。

魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你用一根棍分开它们？要求：尽量在放更多球之后，仍然适用。”

于是博瑟这样分了：

然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营；SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。

现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。

然后，在SVM 工具箱中有另一个更加重要的 trick。魔鬼看到大侠已经学会了一个trick，于是魔鬼给了大侠一个新的挑战。

现在，博瑟没有棍可以很好帮他分开两种球了，现在怎么办呢？博瑟朝桌子一拍，球飞到空中。然后抓起一张纸，插到了两种球的中间。

这里写图片描述

现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了。

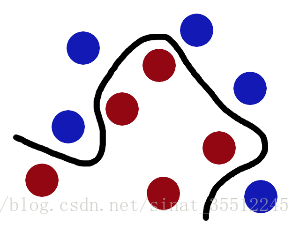
这里写图片描述

再之后，无聊的大人们，把这些球叫做「data」，把棍子叫做「classifier」, 最大间隙trick叫做「optimization」，拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。

from：https://blog.csdn.net/sinat_35512245/article/details/54981721

进入正题.....................

支持向量机学习方法包括构建由简至繁的模型：线性可分支持向量机、线性支持向量机及非线性支持向量机。当训练数据线性可分时，通过硬间隔最大化，学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机；当训练数据近似线性可分时，通过软间隔最大化，也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

1. 什么是支持向量机？

在机器学习领域中，支持向量机”（SVM）是一种可用于分类和回归任务监督学习算法，在实践中，它的主要应用场景是分类。为了解释这个算法，首先我们可以想象一大堆数据，其中每个数据是高维空间中的一个点，数据的特征有多少，空间的维数就有多少。相应的，数据的位置就是其对应各特征的坐标值。为了用一个超平面尽可能完美地分类这些数据点，我们就要用SVM算法来找到这个超平面。在这个算法中，所谓“支持向量”指的是那些在间隔区边缘的训练样本点，而“机”则是用于分类的那个最佳决策边界（线/面/超平面）

给定训练样本集D=(x1,y1),(x2,y2),......(xm,ym),y∈−1,+1，分类学习最基本的想法就是基于训练集D在样本空间中找到一个超平面，将不同类别的样本分开。但是正如下图所示，能将训练样本分开的超平面可能有很多，那我们应该选择哪一个呢？

直观上看，我们应该去找位于两类训练样本“正中间”的超平面，也就是样本点与直线的距离最大那条直线。因为该超平面对训练样本局部扰动的容忍性最好

点到超平面的距离

设二维空间存在一个超平面实现二类可分如下图所示：

在样本空间中，超平面可用如下方程来描述：

$g(x)=w^{T}+b=0$

其中 $w=(w_{1},w_{2},...w_{d})$ 为法向量，决定了超平面的方向；b为位移项，是超平面与远点之间的距离。显然超平面可由法向量w和位移b唯一确定。

一般来说，一个点距离超平面的距离d的大小可以表示分类预测的确信程度。在超平面 $w^{T}+b=0$ 确定的情况下，

$d=\frac{|w^{T}x+b|}{||w||}$

其中，||w||为w的二阶范数

公式（４）也被称为超平面关于样本点xixi的几何间隔 !!!

最大间隔分离超平面

如上图所示，距离超平面最近的这几个训练样本点被称为支持向量，两个异类支持向量（即分别位于超平面两侧的点）到超平面的距离之和为 :

$\gamma =\frac{1}{||w||}+\frac{-1}{||w||}=\frac{2}{||w||}$ $\gamma$ 称为间隔（margin）

要求得最大间隔（即最大化2/w），就是要满足：

问题等价于：

显然，这是个带有约束条件的求极值问题，问题求解在后面。

补充函数间隔与几何间隔的含义：

函数间隔

上一节我们讲到，我们要像线性分类器一样找到一个超平面，不仅能够对数据点进行一个准确的分隔，同时我们希望所有的点尽量都能够远离我们的超平面，即所有点的f(x)值都是很大的正数或者是很小的负数。
但这里就会有一个疑问了，为什么f(x)值能够代表数据点远离超平面的程度呢？接下来，我们将讨论点到超平面的距离问题。

我们的函数间隔定义为：

可以看到，函数间隔其实就是类别标签乘上了f(x)的值，可以看到，该值永远是大于等于0的，正好符合了距离的概念，距离总不能是负的吧。那么为什么该值可以表示数据点到超平面的距离呢？我们不妨这样想，假设y=1,f(x)=1,其实就是将原来的分类超平面f(x) 向右平移了1个单位，而y=1,f(x)=2是将原来的分类超平面f(x) 向右平移了2个单位，所以f(x)值越大的点到分类超平面的距离当然越远，这就解释了我们之前提出的问题。

几何间隔

函数间隔可以表示预测的正确性以及确信度，但是当我们选择最优的超平面的时候，只有函数间隔还不够，主要按照比例改变W和b那么超平面没有变，但是函数间隔却变成了原来的两倍，如将他们改变为 2w 和 2b，虽然此时超平面没有改变，但函数间隔的值 yf (x) 却变成了原来的 4 倍。我们可以对分离超平面的法向量进行约束，例如规范化，||w||=1,这样就使得间隔是确定的，这样函数间隔就变成了几何间隔。

假设B在这条分割线面上，分割线外的一点，到这个平面的距离用表示，任何一个点在这个超平面分割面上都有一个投影，现在假设，A的投影就是B，那么BA就是A到B的距离，w就是它的法向量,其中w/||w||为单位向量，假设A（xi,yi）那么B的x坐标为xi- w/||w||。把B的横坐标带入wTX+b=0,得到：

进一步简化

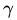
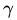
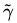
为了得到的绝对值，令乘上对应的类别 y，即可得出几何间隔（用表示）的定义：

几何间隔就是函数间隔除以||w||，而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|，而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。当||w||=1的时候，无乱扩大几倍，对距离都没有影响，这叫做几何距离。

2. 从线性不完全可分到软间隔与松弛变量

(1) 线性不完全可分

由于噪声存在或者数据本身分布有偏差（异常分布的点），现实中大多数情况下，很难实现二类问题的完美划分。如下图所示：

图中，我们很难找到（或者说不存在）一个具有最大边缘(max margin)能够实现红蓝数据点完全分隔且最大间隔内没有数据点分布的超平面。从而造成原来的约束条件无法被满足，无法求解。
(2) 软间隔与松弛变量

针对线性不完全可分的问题，需要引入软间隔(soft margin)的概念：在原来的约束条件上加上一个参数适当放宽原判别准则（限制条件）：

其中，ξi≥0 称为松弛变量。相应地，由于引入了松弛变量，目标函数也得到改变：

其中，为惩罚函数项，对一个异常的点的惩罚（函数）就是这个点到其正确位置（分类判决边界）的距离（如下图所示）：

C为惩罚因子表示异常分布的点对目标函数的贡献权重，C越大表示异常分布的点对目标函数Φ(w)的影响就越大，使得目标函数对异常分布点的惩罚就越大。
因为我们需要 $\frac{1}{2}||w||^{2}$ 尽可能小，同时误分类的异常点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中，需要调参来选择。
至此，我们同样需要求解一个带约束条件的求极值问题：

3. 从线性不可分到特征空间映射与核函数

(1) 线性不可分

线性不可分定义就不说了直接上图0.0：

对于上图的二分类数据点，普通线性分类器不行，最大间隔超平面和软间隔超平面也无能为力。面对这样的线性不可分问题，通常的思路是找出一个非线性分类边界（比如组合分类器）来实现分类。SVM则另辟蹊径，将数据点从原始空间映射到特征空间，而数据在特征空间往往就能实现线性可分。
(2) 特征空间映射

原始空间的线性不可分的数据点，经过映射函数φ(x)到特征空间（往往是低维到高维的映射），往往就能实现线性可分。下面用图举例说明：
① 一维空间向二维空间映射

上图，一维空间不可分，映射到二维空间y=x2y=x2就可以找到一条直线，实现二类完全可分。
② 二维空间向二维特征空间映射

上图，二维空间不可分，但变换一下坐标空间，也能实现线性可分。
③ 二维空间向三维空间的映射

②中的二维空间数据点也能映射到三维空间，同样可以找到一个超平面能够实现在三维空间的线性可分。
(3) 核函数

原始空间向特征空间的映射需要借助映射函数φ(x)。例如对于数据点xi，映射到特征空间就变成了φ(xi)。而SVM的一大巧妙之处就是映射后的特征空间数据点内积的计算等价于低维空间数据点在映射函数对应的核函数中的计算。这大大降低了运算量，因为有的时候高维空间的计算很复杂，下图是一个将mm维向量的映射到特征空间的映射函数的例子：

映射后的维度大概是 $\frac{m^{2}}{2}$ 维。则计算映射后的数据内积的时间复杂度为。而如果使用核函数，则计算复杂度会降低为，例如：

常用的核函数主要有：

① 多项式核函数：

该核函数对应的映射函数为前面的Φ(x)，一个n维的向量映射后的特征空间向量Φ(x)的维度为。
② 高斯核函数：

当xi和xj很接近时，核函数的值约为1；相差很大时，核函数的值约为0。高斯核函数又称为径向基函数。能把原始有限维空间的向量映射到无穷维的特征空间。
③ S型核函数：

类比高斯核函数能够描述两个向量之间的相似度（0~1之间）。双曲正弦函数tanh(⋅)（双极性sigmoid函数）也能作为核函数。同样地，也存在单极性sigmoid核函数。
还有很多其他的核函数，Mercer定理可以判断核函数的有效性。如果我们能够判断出核函数是有效的，甚至不需考虑与之对应的特征映射的函数Φ(x)(实际上Φ(x)很难求)，就能解决特征空间向量的内积的问题。