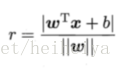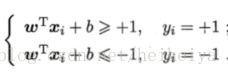一、训练样本线性可分
假设有训练集D={(x1, y1), (x2, y2), ..., (xm, ym)},yi{-1, 1},分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。
但是能将训练样本分开的超平面肯定不止一个。
在样本空间中,超平面可用下面的方程描述:
其中,w=(w1, w2, ..., wd)为法向量,决定了超平面的方向。b为位移项,决定了超平面与原点之间的距离。
样本空间中任意一点x到超平面的距离可以表示为:
假设超平面(w,b)能将训练样本正确分类,令:
距离超平面最近的这几个训练样本点使上式的等式成立。它们被称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为
它被称为“间隔”(margin)。
要寻找具有“最大间隔”的划分超平面,也就是要找到满足约束条件的w,b,使得上式最大,即
等价于:
这就是支持向量机(Support Vector Machine,简称SVM)的基本型。
其对偶问题是:
求解上式的高效算法常用的是SMO。
解出后,求出w和b即可得到模型:
二、训练样本线性不可分
在现实中,原始样本空间内可能不存在一个能正确划分两类样本的超平面。
为解决这个问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内是线性可分的。
令表示将x映射后的特征向量,在特征空间中划分超平面所对应的模型可以表示为:
和线性可分的情况类似:
其对偶问题是:
但是求解上式涉及到计算,这是样本xi和xj映射到特征空间之后的內积。由于特征空间维数可能很高甚至无穷,因此直接计算非常困难。
假设有这样一个函数:
即xi和xj映射到特征空间之后的內积等于它们在原始样本空间中通过函数k(.,.)计算的结果。所以:
求解后即可得到:
这里的函数k(.,.)称为“核函数”(kernel function)。
下面是几种常用的核函数。