机器学习：SVM算法的对偶形式

楔子

广义拉格朗日函数

问题：

转化为无约束的拉格朗日形式：

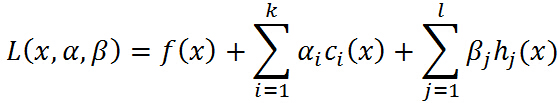
原问题和对偶问题

primal problem opt (原始问题最优化（极小值）):

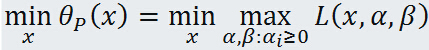
dual problem opt (对偶问题最优化（极大值）):

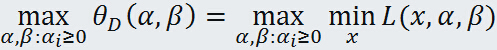
KKT条件

关于KKT 条件的理解：前面三个条件是由解析函数的知识，对于各个变量的偏导数为0（这就解释了一开始为什么假设三个函数连续可微，如果不连续可微的话，这里的偏导数存不存在就不能保证），后面三个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束。剩下一个就是***对偶互补条件***，就是添加项每一项均为0.

SVM对偶形式推导

我们以软间隔为例：

原始优化问题

原问题拉格朗日函数：

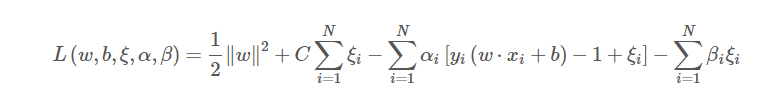
对拉格朗日函数对原始问题的变量：w,b及各个 $\xi_i$求偏导，求极小值：

得到结果带入拉格朗日函数，对变量 $\alpha_i$和 $\beta_i$，求极大值

实际上 $\beta_i$和 $\alpha_i$相关的，可以消去 $\beta_i$， $\beta_i$约束为：0<= $\beta_i$<=C。

以上优化变成一个凸二次优化问题，原始问题的解和对偶问题的解满足KKT条件：

硬间隔和软间隔对偶性形式对比

硬间隔对偶形式

软间隔对偶形式

对比

看到没？目标函数一模一样，差别就在于约束条件 $\alpha_i$的取值范围。
对偶形式可以看成样本的线性组合，权重不为0的样本构成了支持向量。
还可以看出对偶性形式样本只以内积的形式出现，这个给核方法提供了可乘之机。

对偶问题的解和原问题的解关系和区别

对偶形式的解为 $\alpha^*$= $(\alpha_1,…,\alpha_N)^T$
容易求出原问题的解为：

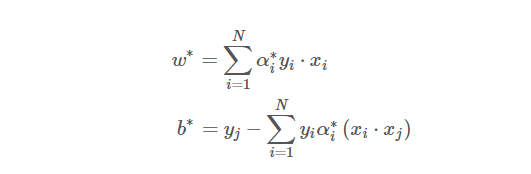
$b^*$表达式中出现的 j 是满足0< $\alpha_j$<C的下标，为什么呢？

首先支持向量一定在 $\alpha_i$>0里面，体会一下：

也就是说由于松弛变量的引入，间隔边界变成一条河了，河里面的点都是支持向量。
所以取0< $\alpha_j$<C， $x_j$必定是在函数间隔上为支持向量，求出的b，就是分割超平面的参数。

$\alpha_i^*$ , $\xi_i^*$,分离超平面位置的关系：