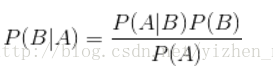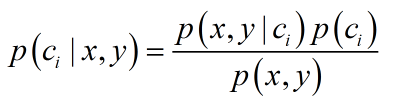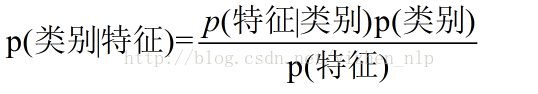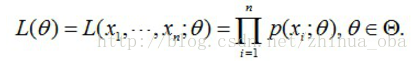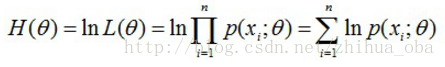最近系统地学习了2008版的CS229,笔记如下
有些凌乱,大家见谅
cost function:
LMS algorithm 最小均方算法
为了找到使得cost function最小的θ,我们考虑使用梯度下降法
这个方法就是从某一个 θ 的初始值开始,然后逐渐重复更新
上面的这个更新要同时对应从 0 到 n 的所有j 值进行。
这里的 α 也称为学习速率。这个算法是很自然的,逐步重复,朝向 J 降低最快的方向移动。
要实现这个算法,咱们需要解决等号右边的导数项。首先来解
决只有一组训练样本 (x, y) 的情况,这样就可以忽略掉等号
右边对 J 的求和项目了。公式就简化下面这样:
对单个训练样本,更新规则如下所示:
此规则也称为LMS更新规则
当一个训练集有超过一个训练样本的时候,有两种对这个规则的修改方法。
第一种就是下面这个算法: 重复直到收敛
不难证明,在上面这个更新规则中求和项的值就是
∂J(θ)/∂θ j (这是因为对 J 的原始定义)。所以这个更新规则实际上就是对原始的成本函数 J 进行简单的梯度下降。这一方法在每一个步长内检查所有整个训练集中的所有样本,也叫做批量梯度下降法(batch gradient descent)
此外还有另外一种方法能够替代批量梯度下降法,这种方法效果也不错。如下所示:
在这个算法里,我们对整个训练集进行了循环遍历,每次遇到一个训练样本,根据每个单一训练样本的误差梯度来对参数进行更新。
这个算法叫做随机梯度下降法(stochastic gradientdescent),或者叫增量梯度下降法(incremental gradientdescent)。批量梯度下降法要在运行第一步之前先对整个训练集进行扫描遍历,当训练集的规模 m 变得很大的时候,因此引起的性能开销就很不划算了;随机梯度下降法就没有这个问题,而是可以立即开始,对查询到的每个样本都进行运算。通常情况下,随机梯度下降法查找到足够接近最低值的 θ 的速度要比批量梯度下降法更快一些。
最大似然估计
“似然”是对likelihood 的一种较为贴近文言文的翻译,“似然”用现代的中文来说即“可能性”。故而,若称之为“最大可能性估计”则更加通俗易懂。
最大似然法明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然法是一类完全基于统计的系统发生树重建方法的代表。该方法在每组序列比对中考虑了每个核苷酸替换的概率。
在对数据进行概率假设的基础上,最小二乘回归得到的 θ 和最大似然法估计的 θ 是一致的。所以这是一系列的假设,其前提是认为最小二乘回归(least-squares regression)能够被判定为一种非常自然的方法,这种方法正好就进行了最大似然估计
高斯判别模型(GDA)
高斯判别模型能比逻辑回归对数据进行更强的建模和假设
高斯判别分析方法(GDA)能够建立更强的模型假设,并且在数据利用上更加有效(比如说,需要更少的训练集就能有“还不错的”效果),当然前提是模型假设争取或者至少接近正确。逻辑回归建立的假设更弱,因此对于偏离的模型假设来说更加健壮(robust)得多。然而,如果训练集数据的确是非高斯分布的(non-Gaussian),而且是有限的大规模数据(in the limit of large datasets),那么逻辑回归几乎总是比GDA要更好的。因此,在实际中,逻辑回归的使用频率要比GDA高得多。
泊松分布
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为
特征函数为
泊松分布与二项分布
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的。
朴素贝叶斯法
(x i 是离散值的时候来使用的一种学习算法)
P(Y|X)是条件概率,在已知X发生概率下,Y发生的概率
要给p(x|y)建模,先来做一个非常强的假设。我们假设特征向量x i 对于给定的 y 是独立的。这个假设也叫做朴素贝叶斯假设(Naive Bayes ,NB assumption),基于此假设衍生的算法也就叫做朴素贝叶斯分选器(Naive Bayes classifier)。例如,如果 y = 1 意味着一个邮件是垃圾邮件;然后其中“buy” 是第2087个单词,而 “price”是第39831个单词;那么接下来我们就假设,如果我告诉你 y = 1,也就是说某一个特定的邮件是垃圾邮件,那么对于x 2087 (也就是单词 buy 是否出现在邮件里)的了解并不会影响你对x 39831 (单词price出现的位置)的采信值。更正规一点,可以写成 p(x 2087 |y) = p(x 2087 |y, x 39831 )。(要注意这个并不是说x 2087 和 x 39831 这两个特征是独立的,那样就变成了p(x 2087 ) = p(x 2087 |x 39831 ),我们这里是说在给定了 y 的这样一个条件下,二者才是有条件的独立。)
然后我们就得到了等式:
第一行的等式就是简单地来自概率的基本性质,第二个等式则使用了朴素贝叶斯假设。
贝叶斯法则如下:
- 不同于其它分类器,朴素贝叶斯是一种基于概率理论的分类算法;
- 特征之间的条件独立性假设,显然这种假设显得“粗鲁”而不符合实际,这也是名称中“朴素”的由来。然而事实证明,朴素贝叶斯在有些领域很有用,比如垃圾邮件过滤;
- 在具体的算法实施中,要考虑很多实际问题。比如因为“下溢”问题,需要对概率乘积取对数;再比如词集模型和词袋模型,还有停用词和无意义的高频词的剔除,以及大量的数据预处理问题,等等;
拉普拉斯光滑
背景:零概率问题,就是在计算实例的概率时,如果某个量x,在观察样本库(训练集)中没有出现过,会导致整个实例的概率结果是0。在文本分类问题中,当一个词语没有在训练样本中出现,该词语调概率为0,使用连乘计算文本出现概率时也为0。这是不合理的,不能因为一个事件没有观察到就武断的认为该事件的概率是0
拉普拉斯平滑:假定训练样本很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题
Token是一个用户自定义的任意字符串,在文本分类中指“词条”
标称型数据和数值型数据
标称型:一般在有限的数据中取,而且只存在‘是’和‘否’两种不同的结果(一般用于分类)
数值型:可以在无限的数据中取,而且数值比较具体化,例如4.02,6.23这种值(一般用于回归分析)
词集模型和词袋模型
词集模型中一个词中只出现一次,词袋模型中一个词可以出现多次
cost function & loss function
损失函数(Loss function)是定义在单个训练样本上的,也就是就算一个样本的误差,比如我们想要分类,就是预测的类别和实际类别的区别,是一个样本的哦,用L表示
代价函数(Cost function)是定义在整个训练集上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和的平均,有没有这个平均其实不会影响最后的参数的求解结果。
https://blog.csdn.net/zhihua_oba/article/details/73776553
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
极大似然估计
总的来说:极大似然估计就是用来估计模型参数的统计学方法。
(1)举例说明:经典问题——学生身高问题
我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组,然后先统计抽样得到的100个男生的身高。假设他们的身高是服从正态分布的。但是这个分布的均值μ和方差σ2我们不知道,这两个参数就是我们要估计的。记作θ=[μ,σ]T。
问题:我们知道样本所服从的概率分布的模型和一些样本,需要求解该模型的参数。如图1
图1
我们已知的有两个:样本服从的分布模型、随机抽取的样本;我们未知的有一个:模型的参数。根据已知条件,通过极大似然估计,求出未知参数。总的来说:极大似然估计就是用来估计模型参数的统计学方法。
(2)如何估计
问题数学化:设样本集X=x1,x2,…,xN,其中N=100 ,p(xi|θ)为概率密度函数,表示抽到男生xi(的身高)的概率。由于100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积,也就是样本集X中各个样本的联合概率,用下式表示:
这个概率反映了,在概率密度函数的参数是θ时,得到X这组样本的概率。 我们需要找到一个参数θ,使得抽到X这组样本的概率最大,也就是说需要其对应的似然函数L(θ)最大。满足条件的θ叫做θ的最大似然估计量,记为
θ̂ =argmaxL(θ)
(3)求最大似然函数估计值的一般步骤
首先,写出似然函数:
然后,对似然函数取对数:
接着,对上式求导,令导数为0,得到似然方程;
最后,求解似然方程,得到的参数θ即为所求。
Jensen不等式
设f是定义域为实数的函数,如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。
Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么:E[f(X)]≥f(E[X])。当且仅当X是常量时,上式取等号。其中,E[x]表示x的数学期望。
注:
1、Jensen不等式应用于凹函数时,不等号方向反向。当且仅当X是常量时,Jensen不等式等号成立。
2、关于凸函数,百度百科中是这样解释的——“对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上非负,就称为凸函数(向下凸)”。关于函数的凹凸性,百度百科中是这样解释的——“中国数学界关于函数凹凸性定义和国外很多定义是反的。国内教材中的凹凸,是指曲线,而不是指函数,图像的凹凸与直观感受一致,却与函数的凹凸性相反。只要记住“函数的凹凸性与曲线的凹凸性相反”就不会把概念搞乱了”。关于凹凸性这里,确实解释不统一,博主暂时以函数的二阶导数大于零定义凸函数,此处不会过多影响EM算法的理解,只要能够确定何时E[f(X)]≥f(E[X])或者E[f(X)]≤f(E[X])就可以。
EM算法
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation Maximization Algorithm)。EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题
KL-divergence,俗称KL距离,常用来衡量两个概率分布的距离
K-means方法是一种无监督学习的算法,它解决的是聚类问题
k-means算法优缺点分析
优点:
算法简单易实现;
缺点:
需要用户事先指定类簇个数K;
聚类结果对初始类簇中心的选取较为敏感;
容易陷入局部最优;
只能发现球型类簇;
k-means++
k-means++算法选择初始seeds的基本思想就是:初始的聚类中心之间的相互距离要尽可能的远
http://www.cnblogs.com/nocml/p/5150756.html
https://blog.csdn.net/sinat_35512245/article/details/55051306
https://blog.csdn.net/loadstar_kun/article/details/39450615
二分-K均值
二分-K均值是为了解决k-均值的用户自定义输入簇值k所延伸出来的自己判断k数目,
其基本思路是:
为了得到k个簇,将所有点的集合分裂成两个簇,从这簇中选取一个继续分裂些,如此下去,直到产生k个簇。
Softmax与Sigmoid的异同
| Softmax |
Sigmoid |
|
| 公式 |
 |
 |
| 本质 |
离散概率分布 |
非线性映射 |
| 任务 |
多分类 |
二分类 |
| 定义域 |
某个一维向量 |
单个数值 |
| 值域 |
[0,1] |
(0,1) |
| 结果之和 |
一定为1 |
为某个正数 |
Sigmoid就是极端情况(类别数为2)下的Softmax