ng在coursera上的机器学习课已经讲过了PCA,这里不再过多赘述。但是下面要介绍PCA的数据预处理过程,并证明,为什么PCA选取的主成分是协方差矩阵对应的特征值前k大的特征向量。
PCA前的数据预处理
令\(\mu=\frac 1 m \sum_{i=1}^m x^{(i)}\)是m个数据的均值,\(\sigma_j^2=\frac 1 m \sum_{i=1}^m(x_j^{(i)}-\mu_j)^2\)是m个数据第j种特征的方差,做PCA之前,要对所有数据做Z-score归一化:
\[x^{(i)}_j:=\frac {x^{(i)}_j-\mu_j}{\sigma_j}\]
减去均值,保证归一化后的数据均值为0,除以标准差\(\sigma\),保证归一化后的数据,每种特征的标准差都是1
PCA的数学证明

设共有m组数据,\(x^{(i)}\in \mathbb R^n\),即每个数据有n个特征。
PCA的第一步,是要找到k个线性无关的单位向量\(u_1,\cdots,u_k\),使得所有点在\(u_1,\cdots,u_k\)上的投影方差最大,从而保留尽可能多的信息。
比如k=1时,如上图所示,中间这个图选取的单位向量u比右边的图选取的u要好,因为数据点在中图的向量u上的投影方差比右图大。
我们知道,对于单位向量\(u\)而言,向量x在u上的投影\(\mathrm{Prj}_u x=u\cdot x=x^Tu\)(注意方向,向量x与u夹角大于90度时投影为负数)
那么m个点在单位向量u的投影的方差可以表示为:
\[\frac 1 m \sum_{i=1}^m(\mathrm{Prj}_u x^{(i)}-\mu)^2\]
\(\mu\)是m个投影的均值
\[\mu=\frac 1 m \sum_{i=1}^m u^Tx^{(i)}=\frac 1 m u^T\sum_{i=1}^m x^{(i)}\]
由于之前已做过Z-score归一化,所以\(\sum_{i=1}^m x^{(i)}=0\),\(\mu=0\)
所以有:
\[\frac 1 m \sum_{i=1}^m(\mathrm{Prj}_u x^{(i)}-\mu)^2\]
\[=\frac 1 m \sum_{i=1}^m (\mathrm{Prj}_u x^{(i)})^2\]
\[=\frac 1 m \sum_{i=1}^m ((x^{(i)})^Tu)^2\]
\[=\frac 1 m \sum_{i=1}^m u^T(x^{(i)})((x^{(i)})^T)u\]
\[=u^T(\frac 1 m \sum_{i=1}^m x^{(i)}(x^{(i)})^T)u\]
约束条件为\(\|u\|=1\),对于这个带约束条件的优化问题,我们可以使用拉格朗日乘数法,构造拉格朗日函数(\(\alpha\)是拉格朗日乘子)
\[\mathcal L=u^T(\frac 1 m \sum_{i=1}^m x^{(i)}(x^{(i)})^T)u+\alpha (\|u\|^2-1)\]
\(\mathcal{L}\)对向量\(u\)求导,并令其等于0:
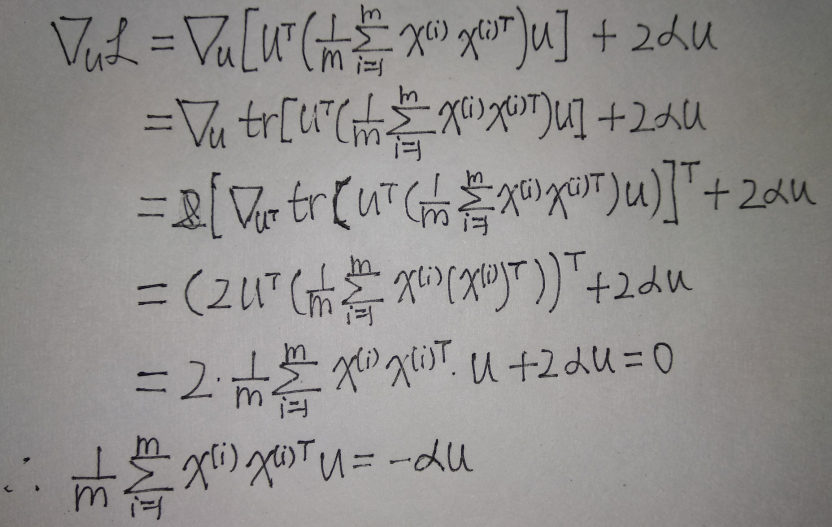
可见u一定是协方差矩阵的特征向量,设\(\Sigma u=\lambda u\),则m个投影的方差
\[u^T(\frac 1 m \sum_{i=1}^m x^{(i)}(x^{(i)})^T)u=u^T\Sigma u=\lambda u^Tu=\lambda \|u\|^2=\lambda\]
这表明\(u\)对应的特征值越大,m个投影的方差越大,越能满足我们的要求。
很容易看出协方差矩阵是实对称阵,有n个线性无关的特征向量,我们可以通过对协方差阵对角化:\(P^{-1}\Sigma P=\Lambda\),其中P是正交阵,P的n个列向量代表n个线性无关且相互正交的、单位化的特征向量。我们只需选P中对应特征值前k大的特征向量作为一组标准基即可