【神经网络和深度学习】吴恩达（Andrew Ng）- 第三周课程总结

一、综述

本文根据吴恩达老师第三周的深度学习课程的课后编程作业来写的，其中涉及到的test_cases.py和planar_utils.py在此处下载。

二、准备工作

2.1 分析问题

我们要做的是：建立一个包含一个隐藏层，一个输出层的神经网络。该神经网的功能与第二周的Logistic Regression回归处理的问题是相似的，都是分类问题。但是，此次的数据集根据单纯的Logistic Resgression回归处理的结果是不太好的，因此使用带有隐藏层的神经网络来处理。

2.2 分析数据

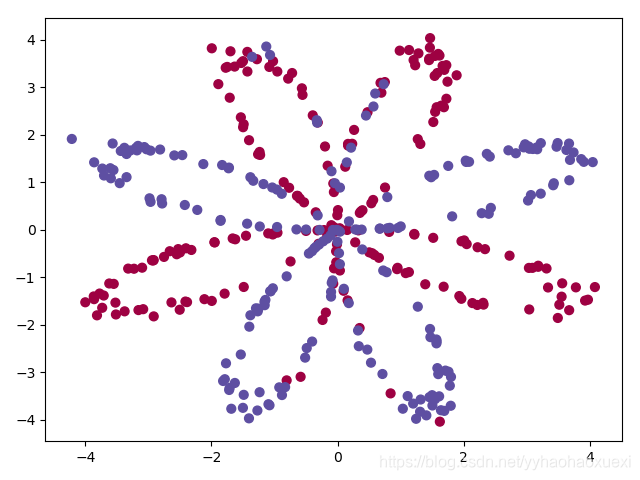
首先，我们查看此次实验的数据：

# 分析数据

X, Y = planar_utils.load_planar_dataset()
print(np.shape(X))
print(np.shape(Y))
# 可视化
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral) #绘制散点图
plt.show()
# 上一语句如出现问题，请使用下面的语句：
# plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral) #绘制散点图

输出：

# X(2, 400)
# 也就说明有两个特征，即X1 X2，一共有400组特征输入
(2, 400)
# Y(1,400)
# 输出分别是400组输入的label
(1, 400)

数据图片

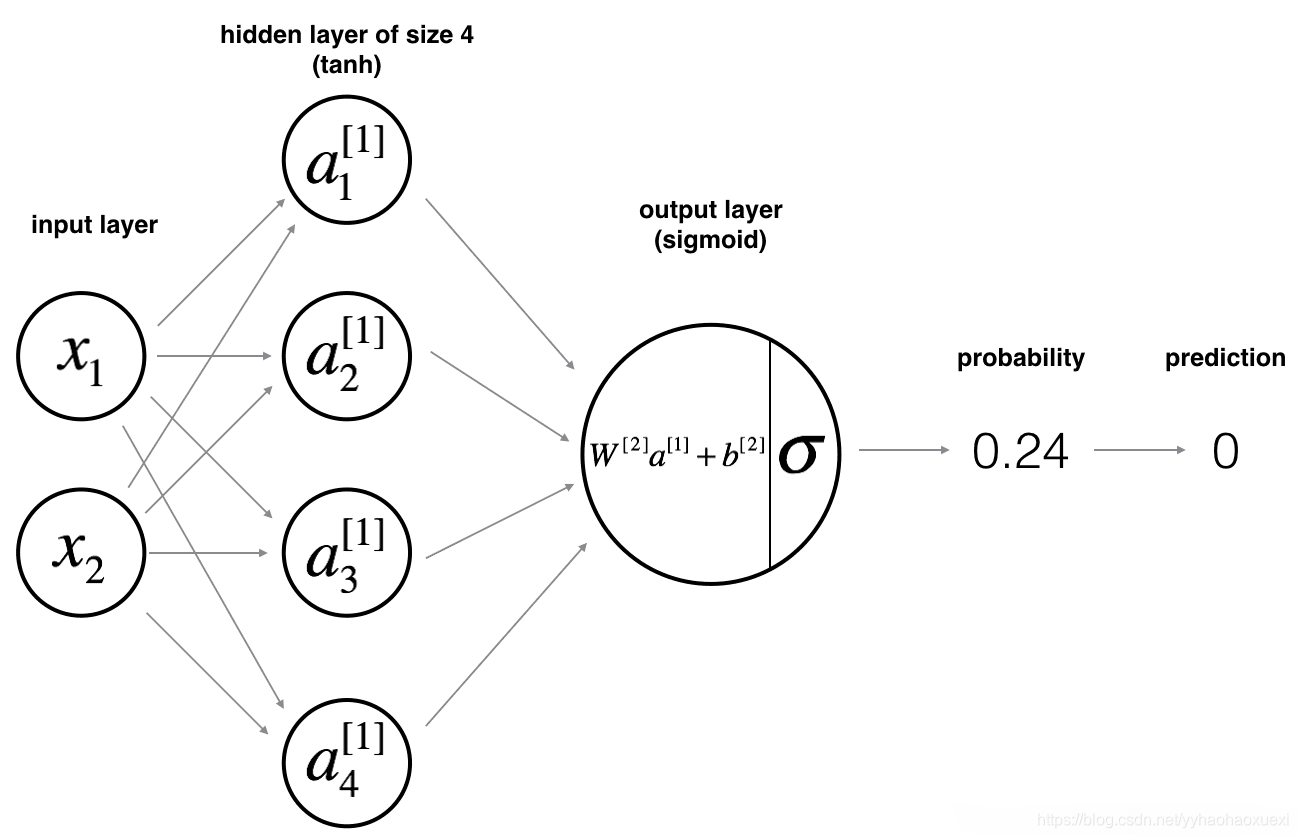
三、分析网络

我们要建立的网络结构如下：

3.1 公式及含义

本次实验涉及到的公式及相关含义：
$z^{[1](i)} = W^{[1]} x^{(i)} + b^{[2](i)} \tag{1}$
$a^{[1](i)} = tanh(z^{[1](i)})\tag{2}$
$z^{[2](i)} = W^{[2]} x^{(i)} + b^{[2](i)} \tag{3}$
$\hat{y}^{(i)} = a^{[2](i)} = sigmoid(z^{[2](i)}) = \sigma(z^{[2](i)}) = \frac{1}{1+e^{-z^{[2](i)}}} \tag{4}$
$y^{(i)}_{prediction} = \begin{cases} 1, \quad\quad\quad y^{(i)} > 0.5 \\ 0, \quad\quad\quad 其它 \end{cases} \tag{5}$
$J = -\frac{1}{m}\sum_{i=0}^{m-1}\Big( y^{(i)}log(\hat y^{(i)})+(1-y^{(i)})log(1- \hat y^{(i)}) \Big)\tag {6}$
其中J是交叉熵损失，在《统计学方法》(李航著)第六章中有详细讲解。其余公式在吴恩达老师的深度学习课程第一课第三周中讲过，如果有什么忘记或者不清楚的，建议及时回看。
（PS：附上PPT中的梯度下降算法更新参数部分的公式）
梯度下降算法公式
其中 $g^{[1]'} = 1-a^2$

四、构建网络

构建网络的一般方法如下：
1.定义神经网络结构（输入特征值个数，隐藏层规模，输出层规模等）
2.初始化模型参数
3.循环优化参数：
3.1 正向传播
3.2 计算损失
3.3 后向传播
3.4 更新参数

4.1 定义神经网络结构

结构如分析网络时的图片，有两个特征输入，隐藏层有四个神经元，输出层有一个神经元，有一个输出值。

# 定义神经网络结构
def init_layer_size(x, y):
    # 输出层数量（特征值个数）
    n_x = x.shape[0]
    # 隐藏层数量（神经元个数）
    n_h = 4
    # 输出层数量
    n_y = y.shape[0]
    return n_x, n_y, n_h

4.2 初始化模型参数

# 初始化模型参数

# n_x :特征值类别
# n_y :输出层输出个数
# n_h :隐藏层神经元个数
def initialize_parameters(n_x, n_y, n_h):

    # 隐藏层
    # n_h个神经元（隐藏层输出个数），n_x个输入
    W1 = np.random.randn(n_h, n_x) * 0.01
    # 加到每个神经元上的，所以是（神经元个数，1）
    b1 = np.zeros(shape=(n_h, 1))

    # 输出层
    # n_y个神经元（输出层输出个数），n_h个输入（来自于隐藏层的输出）
    W2 = np.random.randn(n_y, n_h) * 0.01
    # 加到每个神经元上的，所以是（神经元个数，1）
    b2 = np.zeros(shape=(n_y, 1))

    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))

    res = {
        'W1': W1,
        'b1': b1,
        'W2': W2,
        'b2': b2
    }
    return res

4.3 循环优化参数

4.3.1 正向传播参数

# 正向传播参数

# X 输入
# parameters 参数
def forward_propagation(X, parameters):
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    # W1 (4, 2)
    # X  (2, 400)
    # b1 (4, 1)
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    # A2 (1, 400)
    A2 = sigmoid(Z2)

    # 确保数据的正确性
    assert (A2.shape == (1, X.shape[1]))

    res = {
        'Z1': Z1,
        'A1': A1,
        'Z2': Z2,
        'A2': A2
    }
    return A2, res

4.3.2 计算损失

# 计算交叉熵损失（Cost Function）
# A2 (1, 400)
# Y  (1, 400)
def compute_cost(A2, Y):
    # 训练集组数
    m = Y.shape[1]
    cost = (-1 / m) * np.sum(Y * np.log(A2) + (1 - Y) * (np.log(1 - A2)))  # 成本函数
    cost = float(np.squeeze(cost))

    assert (isinstance(cost, float))

    return cost

4.3.3 反向传播

# 反向传播
def background_propagation(parameters, res, X, Y):
    m = Y.shape[1]

    W1 = parameters['W1']
    W2 = parameters['W2']

    A1 = res['A1']
    A2 = res['A2']

    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)

    dZ1 = np.multiply(np.dot(W2.T, dZ2), (1 - np.power(A1, 2)))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)

    res = {
        'dW1': dW1,
        'db1': db1,
        'dW2': dW2,
        'db2': db2,
    }

    return res

4.3.4 更新参数

# 使用梯度下降算法更新参数
def update_parameters(parameters, res, learning_rate=0.5):
    W1, W2 = parameters['W1'], parameters['W2']
    b1, b2 = parameters['b1'], parameters['b2']

    dW1, dW2 = res['dW1'], res['dW2']
    db1, db2 = res['db1'], res['db2']

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    res = {
        'W1': W1,
        'b1': b1,
        'W2': W2,
        'b2': b2,
    }

    return res

4.4 预测

def predict(parameters, X):
    A2, res = forward_propagation(X, parameters)
    predictions = np.round(A2)
    return predictions

4.5 整合与调用


def model(X, Y, n_h, num_iterations, print_cost=False):

    layer_size = init_layer_size(X, Y)

    # 注意layer_size的参数的位置
    n_x = layer_size[0]
    n_y = layer_size[1]

    parameters = initialize_parameters(n_x, n_y, n_h)
    W1 = parameters['W1']
    b2 = parameters['b2']
    W1 = parameters['W1']
    b2 = parameters['b2']

    for i in range(num_iterations):
        A2, res_4_forward_propagation = forward_propagation(X, parameters)
        costs = compute_cost(A2, Y)
        res_4_background_propagation = background_propagation(parameters, res_4_forward_propagation, X, Y)
        parameters = update_parameters(parameters, res_4_background_propagation, learning_rate=0.5)

        if print_cost:
            if i % 1000 == 0:
                print('第', i, '次循环，成本为：' + str(costs))

    return parameters
    
parameters = model(X, Y, n_h=4, num_iterations=10000, print_cost=True)

4.6 绘制结果

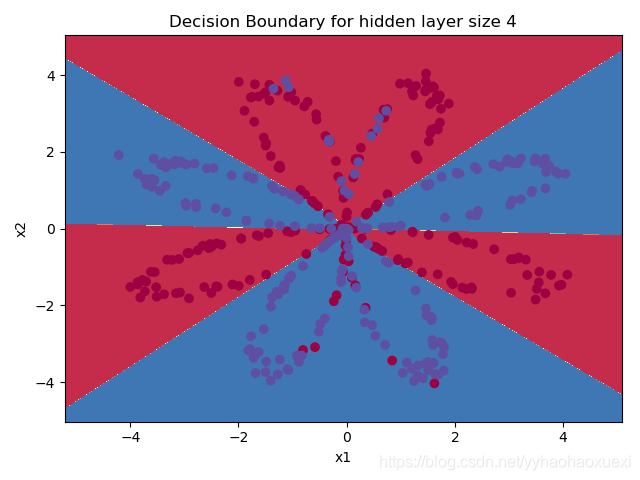
#绘制边界
planar_utils.plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))

predictions = predict(parameters, X)
print('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
plt.show()

X, Y = planar_utils.load_planar_dataset()


plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral) #绘制散点图
plt.show()

输出：

第 0 次循环，成本为：0.6931125167719424
第 1000 次循环，成本为：0.3018260619349989
第 2000 次循环，成本为：0.28671239842926227
第 3000 次循环，成本为：0.27867697737583497
第 4000 次循环，成本为：0.2733112974222824
第 5000 次循环，成本为：0.26926236471810167
第 6000 次循环，成本为：0.2659462203243697
第 7000 次循环，成本为：0.26305193251429543
第 8000 次循环，成本为：0.2603753013304441
第 9000 次循环，成本为：0.25760866918830294
准确率: 90%

结果图片