Dinic算法（研究总结，网络流）

网络流是信息学竞赛中的常见类型，笔者刚学习了最大流Dinic算法，简单记录一下

网络流基本概念

什么是网络流

在一个有向图上选择一个源点，一个汇点，每一条边上都有一个流量上限（以下称为容量），即经过这条边的流量不能超过这个上界，同时，除源点和汇点外，所有点的入流和出流都相等，而源点只有流出的流，汇点只有汇入的流。这样的图叫做网络流。

所谓网络或容量网络指的是一个连通的赋权有向图 D= （V、E、C），其中V 是该图的顶点集，E是有向边(即弧)集，C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流，这是定义在网络上的非负函数，它一方面受到容量的限制，另一方面除去起点和终点以外，在所有中途点要求保持流入量和流出量是平衡的。（引自百度百科）

定义

我们定义：
源点：只有流出去的点
汇点：只有流进来的点
流量：一条边上流过的流量
容量：一条边上可供流过的最大流量
残量：一条边上的容量-流量

几个基本性质

基本性质一：

对于任何一条流，总有流量<=容量

这是很显然的

基本性质二

对于任何一个不是源点或汇点的点u，总有
$\sum p \in E k [p] [u] == \sum q \in E k [u] [q] （其中k[i][j]表示i到j的流量）$

这个也很显然，即一个点（除源点和汇点）的入流和出流相等

基本性质三

对于任何一条有向边(u,v)，总有
$k [u] [v] == - k [v] [u]$

这个看起来并不是很好理解，它的意思就是一条边的反边上的流是这条边的流的相反数，可以这么想，就是如果有k[u][v]的流从u流向v，也就相当于有-k[v][u]的流从v流向u。这条性质非常重要。

网络流最大流

网络流的最大流算法就是指的一个流量的方案使得网络中流量最大。

网络流最大流的求解

网络流的所有算法都是基于一种增广路的思想，下面首先简要的说一下增广路思想，其基本步骤如下：

1.找到一条从源点到汇点的路径，使得路径上任意一条边的残量>0（注意是小于而不是小于等于，这意味着这条边还可以分配流量），这条路径便称为增广路
2.找到这条路径上最小的F[u][v]（我们设F[u][v]表示u->v这条边上的残量即剩余流量），下面记为flow
3.将这条路径上的每一条有向边u->v的残量减去flow，同时对于起反向边v->u的残量加上flow（为什么呢？我们下面再讲）
4.重复上述过程，直到找不出增广路，此时我们就找到了最大流

这个算法是基于增广路定理(Augmenting Path Theorem): 网络达到最大流当且仅当残留网络中没有增广路（由于笔者知识水平不高，暂且不会证明）

举个例子：
此处输入图片的描述

为什么要连反向边

我们知道，当我们在寻找增广路的时候，在前面找出的不一定是最优解，如果我们在减去残量网络中正向边的同时将相对应的反向边加上对应的值，我们就相当于可以反悔从这条边流过。
比如说我们现在选择从u流向v一些流量，但是我们后面发现，如果有另外的流量从p流向v，而原来u流过来的流量可以从u->q流走，这样就可以增加总流量，其效果就相当于p->v->u->q，用图表示就是：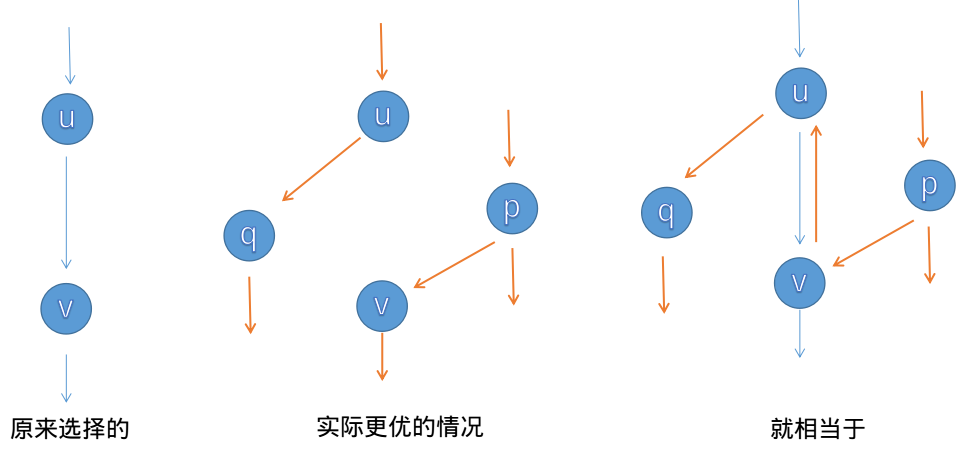
此处输入图片的描述
图中的蓝色边就是我们首次增广时选择的流量方案，而实际上如果是橘色边的话情况会更优，那么我们可以在v->u之间连一条边容量为u->v减去的容量，那我们在增广p->v->u->q的时候就相当于走了v->u这条"边"，而u->v的流量就与v->u的流量相抵消，就成了中间那幅图的样子了。
如果是v->u时的流量不能完全抵消u->v的，那就说明u还可以流一部分流量到v，再从v流出，这样也是允许的。

一个小技巧

虽然说我们已经想明白了为什么要加反向边，但反向边如何具体实现呢？笔者在学习网络流的时候在这里困扰了好久，现在简要的总结在这里。
首先讲一下邻接矩阵的做法，对于G[u][v]，如果我们要对其反向边进行处理，直接修改G[v][u]即可。
但有时会出现u->v和v->u同时本来就有边的情况，一种方法是加入一个新点p，使u->v，而v->u变成v->p,p->u。
另一种方法就是使用邻接表，我们把边从0开始编号，每加入一条原图中的边u->v时，加入边v->u流量设为0，那么这时对于编号为i的边u->v，我们就可以知道i^1就是其反向边v->u。

朴素算法的低效之处

虽然说我们已经知道了增广路的实现，但是单纯地这样选择可能会陷入不好的境地，比如说这个经典的例子：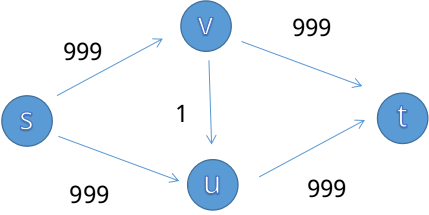
此处输入图片的描述
我们一眼可以看出最大流是999(s->v->t)+999(s->u->t)，但如果程序采取了不恰当的增广策略：s->v->u->t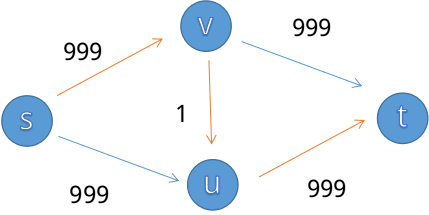

我们发现中间会加一条u->v的边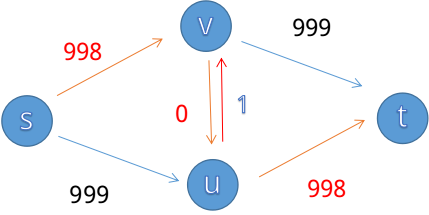

而下一次增广时：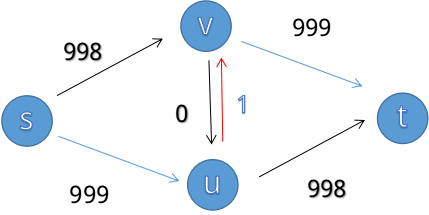

若选择了s->u->v->t

然后就变成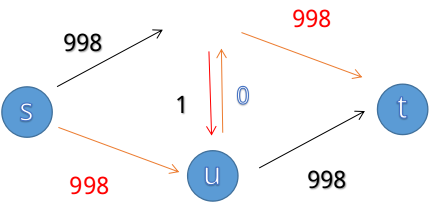

这是个非常低效的过程，并且当图中的999变成更大的数时，这个劣势还会更加明显。
怎么办呢？
这时我们引入Dinic算法

Dinic算法

为了解决我们上面遇到的低效方法，Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点，我们根据从源点开始的bfs序列，为每一个点分配一个深度，然后我们进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。下面给出代码
一些变量的定义

int s,t;//源点和汇点
int cnt;//边的数量，从0开始编号。
int Head[maxN];//每一个点最后一条边的编号 int Next[maxM];//指向对应点的前一条边 int V[maxM];//每一条边指向的点 int W[maxM];//每一条边的残量 int Depth[maxN];//分层图中标记深度

Dinic主过程：

int Dinic()
{
    int Ans=0;//记录最大流量 while (bfs()) { while (int d=dfs(s,inf)) Ans+=d; } return Ans; }

bfs分层图过程

bool bfs()
{
    queue<int> Q;//定义一个bfs寻找分层图时的队列 while (!Q.empty()) Q.pop(); memset(Depth,0,sizeof(Depth)); Depth[s]=1;//源点深度为1 Q.push(s); do { int u=Q.front(); Q.pop(); for (int i=Head[u];i!=-1;i=Next[i]) if ((W[i]>0)&&(Depth[V[i]]==0))//若该残量不为0，且V[i]还未分配深度，则给其分配深度并放入队列 { Depth[V[i]]=Depth[u]+1; Q.push(V[i]); } } while (!Q.empty()); if (Depth[t]==0)//当汇点的深度不存在时，说明不存在分层图，同时也说明不存在增广路 return 0; return 1; }

dfs寻找增广路过程

int dfs(int u,int dist)//u是当前节点，dist是当前流量 { if (u==t)//当已经到达汇点，直接返回 return dist; for (int i=Head[u];i!=-1;i=Next[i]) { if ((Depth[V[i]]==Depth[u]+1)&&(W[i]!=0))//注意这里要满足分层图和残量不为0两个条件 { int di=dfs(V[i],min(dist,W[i]));//向下增广 if (di>0)//若增广成功 { W[i]-=di;//正向边减 W[i^1]+=di;反向边加 return di;//向上传递 } } } return 0;//否则说明没有增广路，返回0 }

把上面的内容都封装到类中：

class Graph
{
private:
    int s,t; int cnt; int Head[maxN]; int Next[maxM]; int V[maxM]; int W[maxM]; int Depth[maxN]; public: int n; void init(int nn,int ss,int tt)//初始化 { n=nn; s=ss; t=tt; cnt=-1; memset(Head,-1,sizeof(Head)); memset(Next,-1,sizeof(Next)); return; } void _Add(int u,int v,int w) { cnt++; Next[cnt]=Head[u]; V[cnt]=v; W[cnt]=w; Head[u]=cnt; } void Add_Edge(int u,int v,int w)//加边，同时加正向和反向的 { _Add(u,v,w); _Add(v,u,0); } int dfs(int u,int dist) { //cout<<"Dfs:"<<u<<' '<<dist<<endl; if (u==t) return dist; for (int i=Head[u];i!=-1;i=Next[i]) { if ((Depth[V[i]]==Depth[u]+1)&&(W[i]!=0)) { int di=dfs(V[i],min(dist,W[i])); if (di>0) { W[i]-=di; W[i^1]+=di; return di; } } } return 0; } int bfs() { //cout<<"Bfs.begin:"<<endl; queue<int> Q; while (!Q.empty()) Q.pop(); memset(Depth,0,sizeof(Depth)); Depth[s]=1; Q.push(s); do { int u=Q.front(); //cout<<u<<endl; Q.pop(); for (int i=Head[u];i!=-1;i=Next[i]) { if ((W[i]>0)&&(Depth[V[i]]==0)) { Depth[V[i]]=Depth[u]+1; Q.push(V[i]); } } } while (!Q.empty()); //cout<<"Bfs.end"<<endl; if (Depth[t]>0) return 1; return 0; } int Dinic() { int Ans=0; while (bfs()) { while (int d=dfs(s,inf)) Ans+=d; } return Ans; } };

Dinic算法的优化

Dinic算法还有优化，这个优化被称为当前弧优化，即每一次dfs增广时不从第一条边开始，而是用一个数组cur记录点u之前循环到了哪一条边，以此来加速
总代码如下，修改的地方已在代码中标出：

class Graph
{
private:
    int cnt; int Head[maxN]; int Next[maxM]; int W[maxM]; int V[maxM]; int Depth[maxN]; int cur[maxN];//cur就是记录当前点u循环到了哪一条边 public: int s,t; void init() { cnt=-1; memset(Head,-1,sizeof(Head)); memset(Next,-1,sizeof(Next)); } void _Add(int u,int v,int w) { cnt++; Next[cnt]=Head[u]; Head[u]=cnt; V[cnt]=v; W[cnt]=w; } void Add_Edge(int u,int v,int w) { _Add(u,v,w); _Add(v,u,0); } int dfs(int u,int flow) { if (u==t) return flow; for (int& i=cur[u];i!=-1;i=Next[i])//注意这里的&符号，这样i增加的同时也能改变cur[u]的值，达到记录当前弧的目的 { if ((Depth[V[i]]==Depth[u]+1)&&(W[i]!=0)) { int di=dfs(V[i],min(flow,W[i])); if (di>0) { W[i]-=di; W[i^1]+=di; return di; } } } return 0; } int bfs() { queue<int> Q; while (!Q.empty()) Q.pop(); memset(Depth,0,sizeof(Depth)); Depth[s]=1; Q.push(s); do { int u=Q.front(); Q.pop(); for (int i=Head[u];i!=-1;i=Next[i]) if ((Depth[V[i]]==0)&&(W[i]>0)) { Depth[V[i]]=Depth[u]+1; Q.push(V[i]); } } while (!Q.empty()); if (Depth[t]>0) return 1; return 0; } int Dinic() { int Ans=0; while (bfs()) { for (int i=1;i<=n;i++)//每一次建立完分层图后都要把cur置为每一个点的第一条边 感谢@青衫白叙指出这里之前的一个疏漏 cur[i]=Head[i]; while (int d=dfs(s,inf)) { Ans+=d; } } return Ans; } };

最大流 dinic