一:实验目的:
1. 掌握LU分解算法原理;
2. 使用C语言编程实现LU分解算法。
二:实验要求
用LU分解算法求解给定的线性方程组 。
函数接口定义:
bool Direct( int n, double a[][MAX_SIZE], double b[] )。
在Direct的接口定义中,n为矩阵a的维数,MAX_SIZE是由裁判程序定义的矩阵最大维数,b是方程组中的常向量,求得的解将存储在b中返回。本题目要求先用杜利特尔分解,再求解两个三角型方程组。函数返回布尔型值,当求解成功时返回TRUE,否则返回FALSE。
实验代码:
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define MAX_SIZE 100 /* 矩阵最大维数 */
#define ZERO 0.000000001 /* 当一个正数小于ZERO就认为该数是0 */
int Direct( int n, double a[][MAX_SIZE], double b[] )
{
double L[MAX_SIZE][MAX_SIZE],U[MAX_SIZE][MAX_SIZE];
double y[MAX_SIZE];
int i,j,k;
double t;
for(i=0;i<n;i++)
{
/*对LU矩阵进行初始化操作*/
L[i][i]=1;
U[0][i]=a[0][i];
for(j=i+1;j<n;j++)
{
L[i][j]=0;
U[j][i]=0;
}
}
for(i=0;i<n;i++)
{
/*求解L矩阵*/
for(k=i+1;k<n;k++)
{
t=0;
for(j=0;j<i;j++)
t=t+L[k][j]*U[j][i];
t=a[k][i]-t;
if(t!=0&&U[i][i]==0)//判断分母是否为零
return 0;
L[k][i]=t/U[i][i];
}
/*求解U矩阵*/
for(k=i+1;k<n;k++)
{
t=0;
for(j=0;j<=i;j++)
t=t+L[i+1][j]*U[j][k];
t=a[i+1][k]-t;
U[i+1][k]=t/L[i+1][i+1];
}
}
/*求解线性方程组LY=b*/
for(i=0;i<n;i++)
{
t=0;
for(j=0;j<i;j++)
t=t+L[i][j]*y[j];
y[i]=b[i]-t;
}
//for(i=0;i<n;i++)
// {
// printf(".8lf\n",y[i]);
// }
/*通过回代法求解线性方程组UX=Y,并将结果放入b[]中*/
for(i=n-1;i>=0;i--)
{
t=0;
for(j=i+1;j<n;j++)
t=t+U[i][j]*b[j];
t=y[i]-t;
if(t!=0&&U[i][i]==0)//判断分母是否为零
return 0;
b[i]=t/U[i][i];
}
return 1;
}
int main()
{
int n, i, j;
double a[MAX_SIZE][MAX_SIZE], b[MAX_SIZE];
while ( scanf("%d", &n) != EOF ) { /* 读取裁判测试用例 */
for ( i=0; i<n; i++ ) {
for ( j=0; j<n; j++ )
scanf("%lf", &a[i][j]);
scanf("%lf", &b[i]);
}
/*--- 输出直接法的解 ---*/
if ( Direct(n, a, b) ) {
printf("Result of direct method:\n");
for ( j=0; j<n; j++ )
printf("%.8lf\n", b[j]);
}
else
printf("Doolittle factorization failed.\n");
printf("\n");
}
return 0;
}
实验结果:


心得体会:

主要是通过等式两边对于元素相等,来将矩阵A分解为一个单位下三角矩阵L和上三角矩阵U。例如
1:通过比较等式两边第一行和第一列可以分别得出:
U(1,j)=a(1,j)(j=1…n)
L(i,1)=a(i,1)/U(1,1)(i=2,..,n)
2:通过比较等式两边第二行和第二列可以得出
U(2,j)=a(i,2)-l(2,1)*U(1,j) j=2,..,n
L(i,2)=(a(i,2)-l(i,1)*U(1,2))/U(2,2) i=3,…,n
因此类推可以得出:
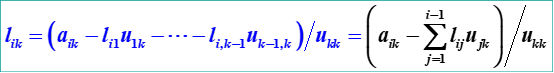
(j=k…,n)
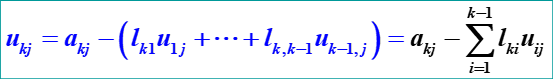
(i=k+1,…,n)
依次到第n步即可求出矩阵L和矩阵U中的所有元素。
在求得LU后,原方程组AX=b即可变为LUX=b的形式。在令UX=Y。
所有原式可以变成:LY=b,和UX=Y。两个线性方程组。又因为LU分别为下三角矩阵和上三角矩阵,因此可以通过直接d代入法求出Y,然后通过回代法求出X。
2:LU分解其实本质是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵,其变换矩阵就是一个单位下三角矩阵。因此若矩阵A可以进行LU分解则应该满足A的顺序主子式不等于零。