线性方程组的解（SVD，正规方程）

非齐次线性方程组Ax=b，A是m*n的矩阵,x是n*1，b是m*1。

   超定：当m>n时，rank(A)=nrank(A,b)    ==>（即b不在A的列向量张成的子空间中）,此时不存在精确解。

                               rank(A)=n=rank(A,b)     ==>（即b在A的列向量张成的子空间中）,此时也存在精确解

   当m=n时，rank(A)=rank(A,b)=n,    ==>存在唯一解。

    当m<n时，rank(A)=rank(A,b)<n,    ==>存在无穷解。

齐次线性方程组Ax=0，A是m*n的矩阵,x是n*1。

    超定：当mn时,rank(A)=n      ==> 存在唯一零解。

    当m<n时,rank(A)<n       ==> 存在无穷解。
 

Ax=b，A是m*n,且m>n.

1) A的秩为n，即A是列满秩的。

解法一：SVD奇异值分解

其中利用了正交变换的保范性质，即一个正交矩阵乘一个矢量，矢量的范数不改变。证明如下，

。

||Ax-b|| = ||UDx-b|| = ||Dx-b||,记和。

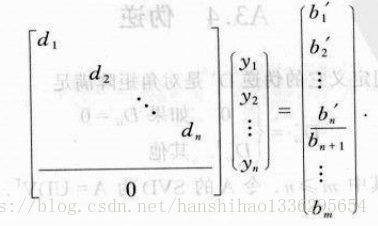
那么问题变为，其中D为m*n的矩阵并且对角线以外元素为零。该方程组的形式为

显然，离最近的Dy是矢量(,,......,,0,....0,由于A的秩为n,那么，可以令得到，进而得到x=Vy。

在伪逆的概念下：

对角矩阵D的伪逆为

那么A=的伪逆为

那么解简写为：

解法二：正规方程

参考最小二乘法的几何意义: 任务是在A的列向量所组成的的子空间中找到接近b的矢量。最接近的情况是Ax是b在A的列空间中的投影，那么Ax-b必然是与A的列空间垂直的矢量，垂直投影指向b。那么Ax-b垂直于A的每一列。

即

,

那么这是一个n*n的线性方程组，称正规方程。

由于A秩为n,为n*n的可逆矩阵。则方程解为

当n相对于m很小时，正规方程解有优势。

2)当A的秩为r<n时，即A不是列满秩的。

待研究。

Ax=0，A是m*n,且m>n.

1) A的秩为n，即A是列满秩的。

解法一：SVD奇异值分解

，

对于齐次方程组，x是方程组的解，那么乘以一个标量k,即kx也是方程组的解，一个约束是求||x||=1的解。

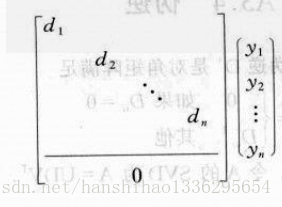
即在约束下求，最小化

令,则问题变成在||y||=1下最小化||Dy||,D是一个按降序排列的对角矩阵，

则解为,.即是V的最后一列，也是的最小特征值的特征矢量。

2)当A的秩为r<n时，即A不是列满秩的。

待研究。