时间序列ARIMA[PYTHON]

【注明】用的是python3.6版本。参考如下三篇博客，增加部分个人理解。
博客1：https://blog.csdn.net/u010414589/article/details/49622625
博客2：https://blog.csdn.net/qq_41214205/article/details/79984095
博客3：https://blog.csdn.net/Tw6cy6uKyDea86Z/article/details/84076363

第一、时间序列的定义：它是一系列在相同时间间隔内测量到的数据点。简言之，时间序列是指以固定的时间间隔记录下的特定的值，时间间隔可以是小时、每天、每周、每10天等等。时间序列的特殊性是：该序列中的每个数据点都与先前的数据点相关。

第二、ARIMA的定义：ARIMA是一种非常流行的时间序列预测方法，它是自回归综合移动平均（Auto-Regressive Integrated Moving Averages）的首字母缩写。ARIMA模型建立在以下假设的基础上：

1、数据序列是平稳的，这意味着均值和方差不应随时间而变化。通过对数变换或差分可以使序列平稳。
2、输入的数据必须是单变量序列，因为ARIMA利用过去的数值预测未来的数值。

ARIMA有三个分量：AR(自回归项)、I(差分项)和MA(移动平均项)。
AR项是指用于预测下一个值的过去值。AR项由ARIMA中的参数‘p’定义。“p”的值是由PACF图确定的。
MA项定义了预测未来值时过去预测误差的数目。ARIMA中的参数‘q’代表MA项。ACF图用于识别正确的‘q’值，
差分顺序规定了对序列执行差分操作的次数，对数据进行差分操作的目的是使之保持平稳。像ADF和KPSS这样的测试可以用来确定序列是否是平稳的，并有助于识别d值。

第三、ARIMA基本建模步骤：

获取被观测系统时间序列数据；
对数据绘图，观测是否为平稳时间序列；对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列；
经过第二步处理，已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF，通过对自相关图和偏自相关图的分析，得到最佳的阶层 p 和阶数 q
由以上得到的d、q、pd、q、p ，得到ARIMA模型。然后开始对得到的模型进行模型检验。

第四、代码详解。（代码部分主要参考博客二）

基本数据导入
from __future__ import print_function
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.api import qqplot
plt.rcParams['font.sans-serif']=['SimHei'] #用来画图时正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  #用来画图时正常显示坐标轴负数
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf


dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422, 
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355, 
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767, 
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232, 
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248, 
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722, 
11999,9390,13481,14795,15845,15271,14686,11054,10395]

dta=np.array(dta,dtype=np.float)  #转换数据类型
dta=pd.Series(dta)

在这里插入图片描述

d阶查分运算
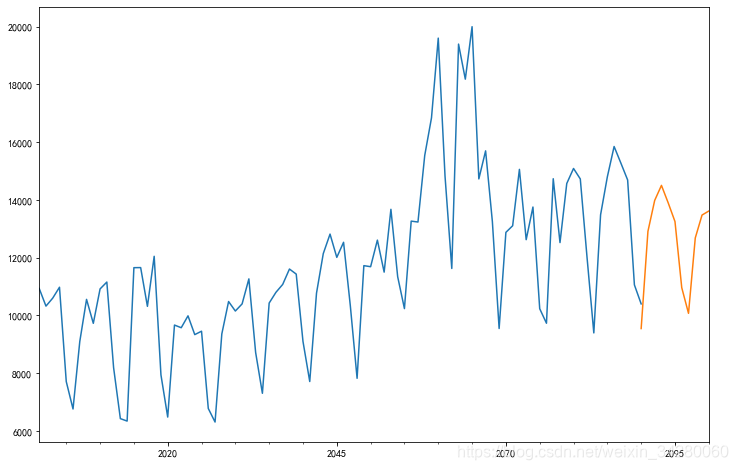
dta.index=pd.Index(sm.tsa.datetools.dates_from_range('2001','2090'))
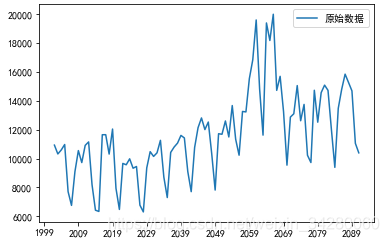
plt.plot(dta,label='原始数据')
plt.legend()  #让label生效

plt.figure()    #新开一个图窗
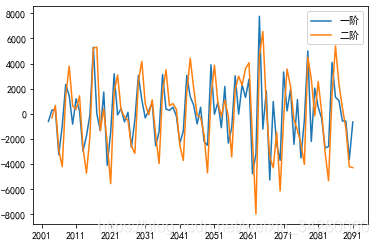
diff1=dta.diff(1)
plt.plot(diff1,label='一阶')
diff2=dta.diff(2)
plt.plot(diff2,label='二阶')
plt.legend()

在这里插入图片描述
肉眼可见：一阶差分的时间序列的均值和方差已经基本平稳，二阶差分后的时间序列与一阶差分相差不大，并且二者随着时间推移，时间序列的均值和方差保持不变。因此可以将差分次数d设置为1。
也可以用单位根检验（Python代码待后续更新）：
ADF检验，如果序列平稳，则不存在单位根，否则就会存在单位根。
若数据不平稳，则可以做差分变换，查看是否差分后平稳。
ADF原假设为，序列存在单位根，即非平稳，对于一个平稳的时序数据，就需要在给定的置信水平上显著，拒绝原假设。
若得到的统计量显著小于3个置信度（1%，5%，10%）的临界统计值时，说明是拒绝原假设的。另外是看P-value是否非常接近0.（4位小数基本即可）

根据得到差分后的平稳序列的acf 图和pacf 图，选择合适的p、q。
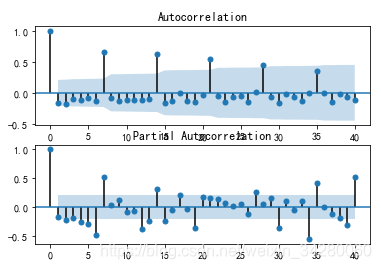
fig=plt.figure()
ax1=fig.add_subplot(211)  # 画子图
plot_acf(diff1[1:],lags=40,ax=ax1)
#diff11=np.diff(dta)
#plot_acf(diff11,lags=40,ax=ax1)
ax2=fig.add_subplot(212)
plot_pacf(diff1[1:],lags=40,ax=ax2)

在这里插入图片描述
通过两图观察得到：

自相关图显示滞后有三个阶超出了置信边界；
偏相关图显示在滞后1至7阶（lags 1,2,…，7）时的偏自相关系数超出了置信边界，从lag 7之后偏自相关系数值缩小至0
根据上图，猜测有以下模型可以供选择：

ARMA(0,1)模型：即自相关图在滞后1阶之后缩小为0，且偏自相关缩小至0，则是一个阶数q=1的移动平均模型；
ARMA(7,0)模型：即偏自相关图在滞后7阶之后缩小为0，且自相关缩小至0，则是一个阶层p=7的自回归模型；
ARMA(7,1)模型：即使得自相关和偏自相关都缩小至零。则是一个混合模型。
…还可以有其他供选择的模型
现在有以上这么多可供选择的模型，我们通常采用ARMA模型的AIC法则。我们知道：增加自由参数的数目提高了拟合的优良性，AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。不仅仅包括AIC准则，目前选择模型常用如下准则：

AIC=-2 ln(L) + 2 k 中文名字：赤池信息量 akaike information criterion
BIC=-2 ln(L) + ln(n)*k 中文名字：贝叶斯信息量 bayesian information criterion
HQ=-2 ln(L) + ln(ln(n))*k hannan-quinn criterion
构造这些统计量所遵循的统计思想是一致的，就是在考虑拟合残差的同时，依自变量个数施加“惩罚”。但要注意的是，这些准则不能说明某一个模型的精确度，也即是说，对于三个模型Ａ，Ｂ，Ｃ，我们能够判断出Ｃ模型是最好的，但不能保证Ｃ模型能够很好地刻画数据，因为有可能三个模型都是糟糕的。

arma_mod70 = sm.tsa.ARMA(dta,(7,0)).fit()
arma_mod01 = sm.tsa.ARMA(dta,(0,1)).fit()
arma_mod71 = sm.tsa.ARMA(dta,(7,1)).fit()
arma_mod80 = sm.tsa.ARMA(dta,(8,0)).fit()
print(arma_mod70.aic,arma_mod70.bic,arma_mod70.hqic)
print(arma_mod01.aic,arma_mod01.bic,arma_mod01.hqic)
print(arma_mod71.aic,arma_mod71.bic,arma_mod71.hqic)
print(arma_mod80.aic,arma_mod80.bic,arma_mod80.hqic)

在这里插入图片描述
可以看出80的aic、bic、hqic均最小。

对残差进行自相关检验
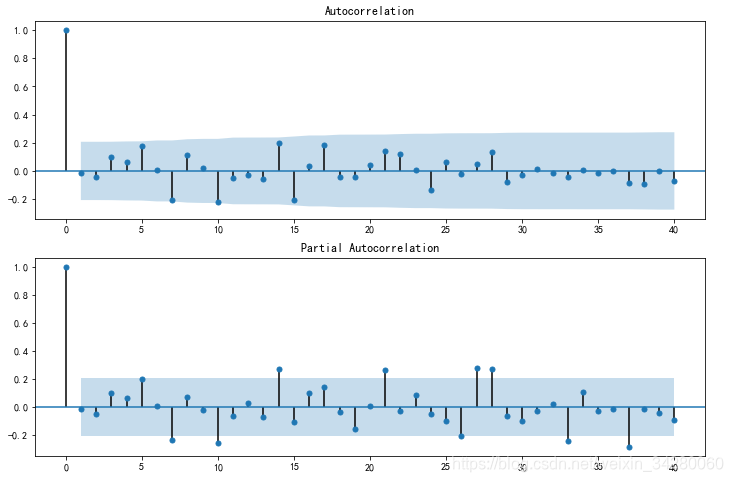
resid = arma_mod80.resid#残差

fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)

print(sm.stats.durbin_watson(arma_mod80.resid.values))

在指数平滑模型下，观察ARIMA模型的残差是否是平均值为0且方差为常数的正态分布（服从零均值、方差不变的正态分布），同时也要观察连续残差是否（自）相关。
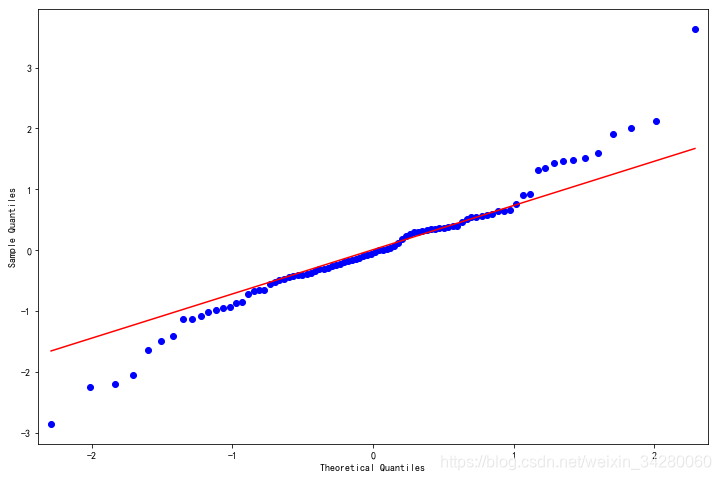
在这里插入图片描述
由图可知：残差的ACF和PACF图，可以看到序列残差基本为白噪声。

残差qq图
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)

在这里插入图片描述

DW检验
print(sm.stats.durbin_watson(arma_mod80.resid.values))

2.02347805932 【不存在自相关性】
德宾-沃森（Durbin-Watson）检验。德宾-沃森检验,简称D-W检验，是目前检验自相关性最常用的方法，但它只使用于检验一阶自相关性。因为自相关系数ρ的值介于-1和1之间，所以 0≤DW≤４。并且DW＝O＝＞ρ＝１　　即存在正自相关性
DW＝４＜＝＞ρ＝－１　即存在负自相关性
DW＝２＜＝＞ρ＝０　　即不存在（一阶）自相关性
因此，当DW值显著的接近于0或４时，则存在自相关性，而接近于２时，则不存在（一阶）自相关性。这样只要知道ＤＷ统计量的概率分布，在给定的显著水平下，根据临界值的位置就可以对原假设Ｈ０进行检验。

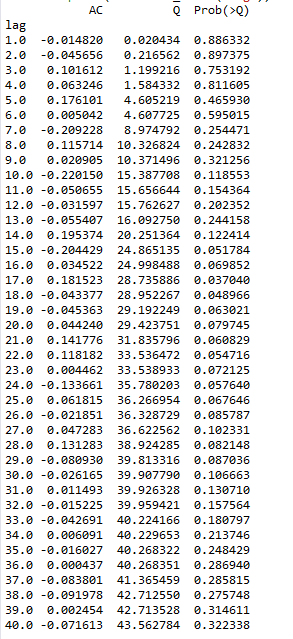
Ljung-Box 检验：LB检验则是基于一系列滞后阶数，判断序列总体的相关性或者说随机性是否存在。 
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))

在这里插入图片描述
检验的结果就是看最后一列前十二行的检验概率（一般观察滞后1~12阶），如果检验概率小于给定的显著性水平，比如0.05、0.10等就拒绝原假设，其原假设是相关系数为零。就结果来看，如果取显著性水平为0.05，那么相关系数与零没有显著差异，即为白噪声序列。即：prob值均大于0.05，所以残差序列不存在自相关性。
在这里插入图片描述

时间序列ARIMA[PYTHON]

猜你喜欢