隐马尔可夫模型学习笔记（一）：前后向算法介绍与推导

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qq_37334135/article/details/86265648

学习隐马尔可夫模型（HMM），主要就是学习三个问题：概率计算问题，学习问题和预测问题。概率计算问题主要是讲前向算法和后向算法，这两个算法可以说是隐马尔可夫的重中之重，接下来会依次介绍以下内容。

1. 隐马尔可夫模型介绍
2. 模型的假设
3. 直接计算法，前向算法，后向算法的介绍与详细推导
4. 根据前后向算法推出一些结论

补充：推导公式很依赖模型的假设与贝叶斯网络，所以在这之前最好了解贝叶斯网络，这两天会补充贝叶斯网络。

学习资料：《统计学习方法》，邹博老师的HMM的ppt，其他。

隐马尔可夫模型

隐马尔可夫模型是关于时序的概率模型。由一个隐藏的马尔可夫链随机生成的不可观测的状态随机序列（理解为隐变量），再由各个状态生成一个观测而产生观测随机序列（理解为显变量）的过程。如下图就是一个隐马尔可夫链，状态序列 $\{Z_1,Z_2,...,Z_{n+1}\}$，再由各个状态序列生成观测序列 $\{X_1,X_2,...,X_{n+1}\}$，而每个节点（位置）对应一个时刻，从前往后就是时刻 $t_1,t_2,...,t_{n+1}$。

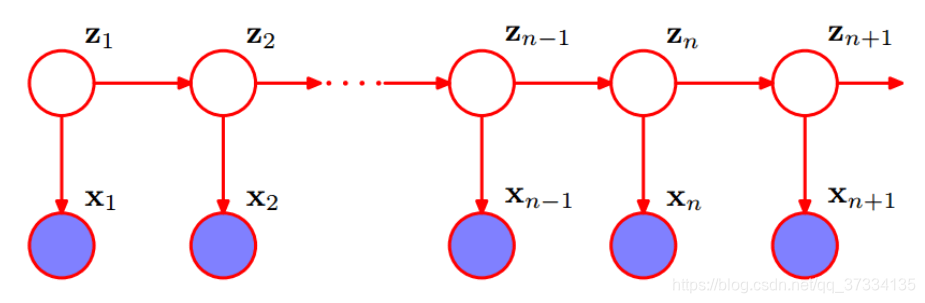
隐马尔可夫模型由初始状态概率向量 $\pi$、状态转移矩阵 $A$和观测矩阵 $B$确定，称为隐马尔可夫三要素，表示为 $\lambda=(\pi,A,B)$，关于具体的参数介绍如下：

记： $Q=\{q_1,q_2,...,q_N\}$表示所有可能的状态集合， $V=\{v_1,v_2,...,v_M\}$表示所有可能的观测集合。

$I=\{i_1,i_2,...,i_T\}$ 表示状态序列， $O=\{o_1,o_2,...,o_N\}$ 为对应的观测序列。

状态转移矩阵 $A$:
令 $a_{ij}=P(i_{t+1}=q_j|i_{t}=q_i)$ 表示 $t$时刻状态为 $q_i$，下一时刻（即 $t+1$）状态为 $q_j$的概率，而状态转移矩阵 $A=(a_{ij})_{N×N}$，注意这里是 $N×N$的方阵。

观测矩阵 $B$:
令 $b_{j}(k)=P(o_t=v_k|i_t=q_j)$表示 $t$时刻状态为 $q_j$的条件下，观测值为 $v_k$的概率，而观测矩阵 $B=(b_{j}(k))_{N×M}$。

初始状态概率向量 $\pi$：
$\pi_i=P(i_1=q_i)$表示初始时刻（即 $t=1$）时状态为 $q_i$的概率。

$\pi,A$决定状态序列， $B$决定观测序列。

由以上定义知，隐马尔可夫做了如下两个假设（两个基本性质）：

1. 齐次马尔可夫假设：任意时刻 $t$的状态只与前一时刻 $t-1$的状态有关，而与其他时刻状态、观测记忆时刻无关，即:
   $P(i_t|i_{t-1},o_{t-1},...,i_1,o_1)=P(i_t|i_{t-1})$
2. 观测独立性假设： 任意时刻的状态只与该时刻马尔可夫链的状态有关，即：
   $P(o_t|i_{T},o_{T},...,i_1,o_1)=P(o_t|i_{t})$

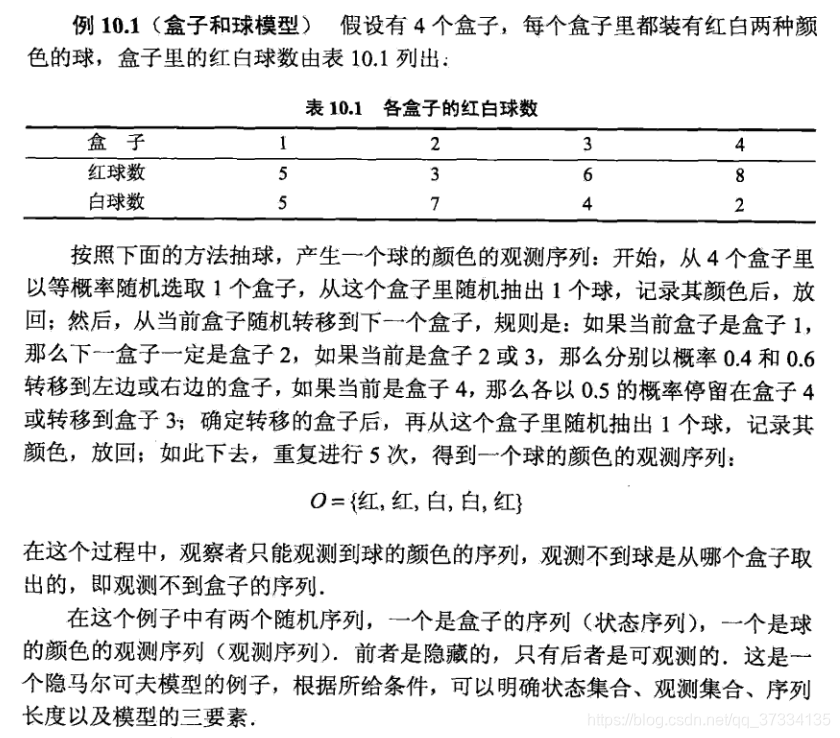
下面给出《统计学习方法》上的盒子和球的例子

三个基本问题

隐马尔可夫模型有三个基本问题：

1. 概率计算问题
2. 学习问题
3. 预测问题

在这里就只讲概率计算问题，后面会接着讲学习问题和预测问题。

概率计算问题指的是给定模型 $\lambda=(\pi,A,B)$和观测序列 $O=\{o_1,o_2,...,o_N\}$，求在模型 $\lambda$下，观测序列 $O$出现的概率，即 $P(O|\lambda)$，下面会介绍三个方法来讲述，分别为

1. 直接计算法
2. 前向算法
3. 后向算法

1、直接计算法

给定模型 $\lambda=(\pi,A,B)$和观测序列 $O=\{o_1,o_2,...,o_N\}$，计算 $P(O|\lambda)$。

$P(O|\lambda)=\sum\limits_{I}P(I|\lambda)P(O|I,\lambda)$

补充：根据贝叶斯网络，对于任意随机变量有 $P(x_1,x_2,...,x_N)=P(x_N|x_1,...,X_{N-1})...P(x_2|x_1)P(x_1)$

计算 $P(I|\lambda)$:

$P(I|\lambda)=P(i_1,i_2,...,i_T|\lambda)=P(i_1|\lambda)P(i_2,...,i_T|i_1,\lambda)=\pi_{i_1}P(i_3,...,i_T|i_2,i_1,\lambda)P(i_2|i_1,\lambda)=\pi_{i_1}a_{i_1i_2}P(i_3,...,i_T|i_2,i_1,\lambda)$

由于状态2给定条件下，状态1和其它状态条件独立（这点由贝叶斯网络得出，或者根据HMM的齐次性假设， $i_3,...,i_T$与 $i_1$是相互独立的），所以 $P(i_3,...,i_T|i_2,i_1,\lambda)=P(i_3,...,i_T|i_2,\lambda)$，所以有

$P(I|\lambda)=\pi_{i_1}a_{i_1i_2}P(i_3,...,i_T|i_2,\lambda)=\pi_{i_1}a_{i_1i_2}P(i_4,...,i_T|i_3,i_2,\lambda)P(i_3|i_2,\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}P(i_4,...,i_T|i_3,i_2,\lambda)=...=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}...a_{i_{T-1}i_T}$

计算 $P(O|I,\lambda)$：

根据HMM的独立性假设得到如下的式子
$P(O|I,\lambda)=P(o_1,o_2,...,o_T|i_1,i_2,...,i_T,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)...b_{i_T}(o_T)$

最终得到 $P(O|\lambda)=\sum\limits_{I}P(I|\lambda)P(O|I,\lambda)=\sum\limits_{i_1,i_2,...,i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)a_{i_2i_3}...a_{i_{T-1}i_T}b_{i_T}(o_T)$

考虑以下时间复杂度： $\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)a_{i_2i_3}...a_{i_{T-1}i_T}b_{i_T}(o_T)$一共是 $2T$个因子，那么就是 $2T-1$个乘号，而外层求和符号是 $T$层，每个状态 $i$有 $N$种取法（状态），所以取法是 $N^T$种，所以时间复杂度是 $O((2T-1)N^T)$ 即 $O(TN^T)$，这个时间复杂度是很恐怖的，并不可取，考虑以下的有效方法：前向算法、后向算法。

2、前向算法

前向算法实际上算作是动态规划算法，也就是将大问题分解分众多小问题，通过小问题的解来得到大问题的解。对各个小问题进行求解后，会将结果保存下来，下次要用的时候就不用再去计算而是直接拿来用了，这样能有效避免重复计算问题，基本上都会涉及到递推。具体的可以去leetcode上刷两题感受一下。

前向概率： 给定隐马尔科夫模型 $\lambda$，定义到时刻 $t$的观测序列为 $o_1,o_2,...,o_t$ 且状态为 $i_t=q_i$的概率为前向概率，记做 $a_t(i)$，表示如下：

$\alpha_t(i)=P(o_1,o_2,...,o_t,i_t=q_i|\lambda)$

为什么要给这么个定义呢，因为我们要求的是 $P(O|\lambda)=P(o_1,o_2,...,o_T|\lambda)$

$\alpha_T(i)=P(o_1,o_2,...,o_T,i_T=q_i|\lambda)$，得到
$\alpha_T(1)+\alpha_T(2)+...+\alpha_T(N)\\=P(o_1,o_2,...,o_T,i_T=q_1|\lambda)+P(o_1,o_2,...,o_T,i_T=q_2|\lambda)...+P(o_1,o_2,...,o_T,i_T=q_N|\lambda)\\=P(o_1,o_2,...,o_T|\lambda)$

最后一个等号根据全概率公式得来。

所以我们可以先对每个 $i=1,2,...,N$求出 $\alpha_1(i)$，从而递推得到 $\alpha_T(i)$，下面看递推公式是怎样的。即，对于每个 $i=1,2,...,N$求出了 $\alpha_t(i)$，那么 $\alpha_{t+1}(i)$是怎么得到的。

前面说了根据贝叶斯网络有： $P(A,B,C)=P(A|B,C)P(B|C)P(C)$

$\alpha_t(j)a_{ji}=P(o_1,o_2,...,o_t,i_t=q_j|\lambda)P(i_{t+1}=q_i|i_t=q_j,\lambda)=P(o_1,o_2,...,o_t|i_t=q_j,\lambda)P(i_{t+1}=q_i|i_t=q_j,\lambda)P(i_t=q_j|\lambda)$

由于 $P(o_1,o_2,...,o_t|i_t=q_j\lambda)=P(o_1,o_2,...,o_t|i_t=q_j,i_{t+1}=q_i,\lambda)$这个在前面的直接计算法中已经说了。所以有
$\alpha_t(j)a_{ji}=P(o_1,o_2,...,o_t|i_t=q_j,i_{t+1}=q_i,\lambda)P(i_{t+1}=q_i|i_t=q_j,\lambda)P(i_t=q_j|\lambda)=P(o_1,o_2,...,o_t，i_t=q_j，i_{t+1}=q_i|\lambda)$
表示在时刻 $t$生成的观测序列 $o_1,o_2,...,o_t$且状态为 $q_j$同时在 $t+1$时刻的状态为 $q_i$的联合概率。（不写推导，直观上也能理解，在后面会不加解释的给出一些式子，因为直观上是容易理解的）。

从而 $\sum\limits_{j=1}^{N}\alpha_t(j)a_{ji}=\sum\limits_{j=1}^{N}P(o_1,o_2,...,o_t，i_t=q_j，i_{t+1}=q_i|\lambda)=P(o_1,o_2,...,o_t,i_{t+1}=q_i|\lambda)$
表示在时刻得到的观测序列为 $o_1,o_2,...,o_t$并且在时刻 $t+1$得到的状态为 $q_i$的联合概率。

$b_i(o_{t+1})=P(o_{t+1}|i_{t+1}=q_i,\lambda)$

从而得到 $(\sum\limits_{j=1}^{N}\alpha_t(j)a_{ji})b_i(o_{t+1})=P(o_1,o_2,...,o_t,i_{t+1}=q_i|\lambda)P(o_{t+1}|i_{t+1}=q_i,\lambda)=P(o_1,o_2,...,o_t|i_{t+1}=q_i,\lambda)P(o_{t+1}|i_{t+1}=q_i,\lambda)P(i_{t+1}=q_i|\lambda)$

根据隐马尔可夫模型的独立性假设得到 $P(o_1,o_2,...,o_t|i_{t+1}=q_i,\lambda)=P(o_1,o_2,...,o_t|i_{t+1}=q_i,o_{t+1}\lambda)$，带入到上式同时根据贝叶斯网络得到：
$(\sum\limits_{j=1}^{N}\alpha_t(j)a_{ji})b_i(o_{t+1})=P(o_1,o_2,...,o_t|i_{t+1}=q_i,o_{t+1}\lambda)P(o_{t+1}|i_{t+1}=q_i,\lambda)P(i_{t+1}=q_i|\lambda)=P(o_1,o_2,...,o_t,o_{t+1},i_{t+1}=q_i)=\alpha_{t+1}(i)$

到这里基本就知道前向算法怎么得到 $P(O)$了，下面写出正式的流程。

前向算法：

输入：隐马尔可夫模型 $\lambda$，观测序列 $O=\{o_1,o_2,...,o_T\}$
输出： 观测序列的概率 $P(O|\lambda)$

（1）、对于每个 $i=1,2,...,N$计算时刻 $t=1$ 初值:

$\alpha_1(i)=P(o_1,i_1=q_i|\lambda)\\=P(o_1|i_1=q_i,\lambda)P(i_1=q_i|\lambda)\\=\pi_ib_i(o_1)$

（2）、递推 对每个 $t=1,2,...,T-1$ 计算

$\alpha_{t+1}(i)=(\sum\limits_{j=1}^{N}\alpha_t(j)a_{ji})b_i(o_{t+1}),i=1,2,...,N$

（3）、终止，计算最终结果：

$P(O|\lambda)=\sum\limits_{i=1}^{N}\alpha_T(i)$

再来考虑前向算法的时间复杂度，看第二步就行，最外层对 $t$进行遍历，第二层对 $i$进行遍历，循环体粗略算是 $N$个乘号，所以最终时间复杂度为 $TN^2$，相比于直接计算的方法时间复杂度降低了太多，那么再来看后向算法。

3、后向算法

后向算法就不写的那么详细了，具体的推导就不写的太详细了。

后向概率： 给定隐马尔可夫模型 $\lambda$，定义在时刻 $t$ 状态为 $q_i$的条件下，从 $t+1$ 到 $T$ 部分的概率为后向概率，记做 $\beta_t(i)$

$\beta_t(i)=P(o_{t+1},...,o_{T}|i_{t}=q_i,\lambda)$

那么根据后向概率怎么得到观测序列的概率 $P(O)$呢？

$\pi_i b_i(o_1)\beta_1(i)=P(i_1=q_i|\lambda)P(o_1|i_1=q_i,\lambda)P(o_{2},...,o_{T}|i_{1}=q_i,\lambda)$
同样也是根据贝叶斯网络那个公式，以及HMM的假设得到：
$\pi_i b_i(o_1)\beta_1(i)=P(i_1=q_i|\lambda)P(o_1|i_1=q_i,\lambda)P(o_{2},...,o_{T}|i_{1}=q_i,o_1,\lambda)=P(o_1,o_{2},...,o_{T},i_1=q_i|\lambda)$

根据全概率公式，那么有 $\sum\limits_{i=1}^{N}P(o_1,o_{2},...,o_{T},i_1=q_i|\lambda)=P(o_1,o_{2},...,o_{T}|\lambda)=P(O|\lambda)$，这不就得到了么。

首先规定 $\beta_T(i)=1$，那么主要是通过递推得到 $\beta_1(i)$。也就是有 $\beta_{t+1}(i)$怎么推到 $\beta_{t}(i)$。

$\beta_{t}(i)=\sum\limits_{j=1}^{N} a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$

这个是怎么来的可以直观理解也可以推导试试，下面给出正式的算法。

后向算法：

输入：隐马尔可夫模型 $\lambda$，观测序列 $O=\{o_1,o_2,...,o_T\}$
输出： 观测序列的概率 $P(O|\lambda)$

（1）、对于每个 $i=1,2,...,N$计算时刻 $t=1$ 初值规定:

$\beta_T(i)=1$

（2）、递推 对每个 $t=T-1,T-2,...,1$ 计算

$\beta_{t}(i)=\sum\limits_{j=1}^{N} a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$

（3）、终止，计算最终结果：

$P(O|\lambda)=\sum\limits_{i=1}^{N}\pi_i b_i(o_1)\beta_1(i)$

考虑时间复杂度，和前向算法是一样的。如果前向和后向算法放在一起的话，我们会得到下面的一些结论。

一些结论

结论1、 $P(O,i_t=q_i|\lambda)=\alpha_t(i)\beta_t(i)$

$P(O,i_t=q_i|\lambda)=P(o_1,o_2,...,o_t,o_{t+1},...,o_T|i_t=q_i,\lambda)P(i_t=q_i|\lambda)$
由于给定 $i_t=q_i$，那么序列 $o_1,o_2,...,o_t$ 和序列 $o_{t+1},...,o_T$ 是条件独立的，所以 $P(o_1,o_2,...,o_t,o_{t+1},...,o_T|i_t=q_i,\lambda)=P(o_1,o_2,...,o_t|i_t=q_i,\lambda)P(o_{t+1},...,o_T|i_t=q_i,\lambda)$，带入上式子得到

$P(O,i_t=q_i|\lambda)=P(o_1,o_2,...,o_t|i_t=q_i,\lambda)P(o_{t+1},...,o_T|i_t=q_i,\lambda)P(i_t=q_i|\lambda)\\=P(o_1,o_2,...,o_t,i_t=q_i|\lambda)P(o_{t+1},...,o_T|i_t=q_i,\lambda)\\=\alpha_t(i)\beta_t(i)$

得到的结论是 $P(O,i_t=q_i|\lambda)=\alpha_t(i)\beta_t(i)$，根据这个结论可以得到下面两个结论

结论2、 $\gamma_t(i)=\frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{i=1}^{N}\alpha_t(i)\beta_t(i)}$

记 $\gamma_t(i)=P(i_t=q_i|O,\lambda)$，即已知模型 $\lambda$，给定观测序列条件下，在 $t$ 时刻状态为 $q_i$ 的概率。

$\gamma_t(i)=P(i_t=q_i|O,\lambda)\\=\frac{P(i_t=q_i,O|\lambda)}{P(O|\lambda)}\\=\frac{P(i_t=q_i,O|\lambda)}{\sum\limits_{i=1}^{N}P(i_t=q_i,O|\lambda)}\\=\frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{i=1}^{N}\alpha_t(i)\beta_t(i)}$

结论3、

记 $\xi_t(i,j)=P(i_t=q_i,i_{t+1}=q_j|O,\lambda)$，即已知模型 $\lambda$和观测 $O$，在时刻 $t$ 处于 $q_i$状态，时刻 $t+1$处于 $q_j$ 状态的概率。

根据后向算法的递推公式可以得到

$a_{ij}b_j(o_{t+1})\beta_{t+1}(i)=P(o_{t+1},o_{t+2},...,o_{T},i_{t+1}=q_j|i_t=q_i,\lambda)$
那么
$\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(i)\\=P(o_1,o_2,...,o_t,i_t=q_i|\lambda)P(o_{t+1},o_{t+2},...,o_{T},i_{t+1}=q_j|i_t=q_i,\lambda)\\=P(o_1,o_2,...,o_t|i_t=q_i,\lambda)P(i_t=q_i|\lambda)P(o_{t+1},o_{t+2},...,o_{T},i_{t+1}=q_j|i_t=q_i,\lambda)\\=P(o_1,...,o_t,o_{t+1},o_{t+2},...,o_{T},i_{t+1}=q_j|i_t=q_i,\lambda)P(i_t=q_i|\lambda)\\=P(o_1,...,o_t,o_{t+1},o_{t+2},...,o_{T},i_t=q_i,i_{t+1}=q_j|\lambda)\\=P(O,i_t=q_i,i_{t+1}=q_j|\lambda)$

注意：第二个等号到第三个等号的成立的原因是在 $i_t=q_i$的条件下， $o_1,o_2,...,o_t$和 $o_{t+1},o_{t+2},...,o_{T},i_{t+1}=q_j$ 是条件独立的。

$\xi_t(i,j)=P(i_t=q_i,i_{t+1}=q_j|O,\lambda)\\=\frac{P(i_t=q_i,i_{t+1}=q_j,O|\lambda)}{P(O|\lambda)}\\=\frac{P(i_t=q_i,i_{t+1}=q_j,O|\lambda)}{\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}P(i_t=q_i,i_{t+1}=q_j,O|\lambda)}\\=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(i)}{\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(i)}$