1.简介
马尔可夫模型是一种无记忆的模型,即在序列中t时刻状态只和t-1时刻相关,这是一种直接的关系。所谓的隐马尔可夫模型说的就是t时刻的状态和t-1时刻间接相关,也就是说两个观测变量之间并没有直接的关系,但是他们的隐藏变量序列符合马尔科夫性质。很多看似不相关的事物中,都会有一种隐性的关系。要了解这种隐性关系,就需要找到隐藏变量,并且发现其中的规律。这确实是一种很迷人的理论,他让我感到了更多的可能性。
2.隐马尔可夫模型

三个参数:上面的图展示了隐马尔可夫的工作流程,X作为隐变量序列,Y作为观测序列。我们将模型参数定义为:λ=(π,A,B),其中π表示初始状态概率分布,即x在第一个时刻的概率分布;A表示转移矩阵,即X之间的参数;B表示发射矩阵,即X和Y之间的参数;有了这三个参数,我们能够表示出x,y的所有变化的可能性。
二个假设:齐次马尔科夫假设(X在t时刻的状态只和t-1时刻有关)和观测独立假设(yt只和xt有关)
三个问题:隐马尔科夫有三个经典的问题,对应于它能够处理的三种情况。总结起来就是Evaluation评估问题,Learning学习问题,Decoding解码问题;
Evaluation就是求给定λ下Y的条件概率(即使用模型参数求观测值);Learning就是给定Y求λ(即给定观测数据,学习模型参数);Decoding就是已知λ和Y求X(即已知模型参数和观测值,求隐变量);
接下来我们详细介绍一下这三个问题。
3.Evaluation
前向算法可以理解为从左到右每个时刻每种状态前向概率之和,后向算法是从右到左每个时刻每种状态后向概率之和。最终都可以表示出参数λ对应观测值的条件概率分布。下面我们详细解释一下。
1.前向算法

直接暴力求解:
对于evaluation问题来说,我们已知参数λ和观测序列的值,要求的是参数λ下观测序列的概率分布,即P(Y|λ),最直接的办法就是求出P(X|λ),再求出P(Y|X,λ),我们得到了隐变量和观测值之间的联合概率。那么再使用边缘概率分布(固定一个变量时,另外一个变量的概率)就可以简单的求出P(Y|λ)
但是这个算法需要去遍历隐层序列所有组合的可能性,整个算法的复杂度是指数级的,假设隐藏状态数为N,隐藏序列长度为T,复杂度就是。这里的复杂度解释一下,序列的组合方式有
中,每个序列需要计算T次。对于数量较少的隐藏单元和状态数来说,这是可以接受的。但是隐藏单元和状态数量很多的情况下,这样的计算成本是致命的。
为了解决这个问题,我们决定另辟蹊径。于是我们召唤来了前向算法。
前向算法:
前向算法的思想很简单,既然参数λ是已知的,我们定义隐变量序列为I,观测序列为O
1.第一个时刻前向概率:时刻一的前向概率=π*发射矩阵;
![]()
2. 后面时刻的前向概率:t+1时刻的前向概率=t时刻的前向概率*状态转移矩阵*发射矩阵
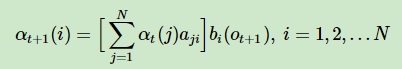
3.最终我们把每一时刻的前向概率加和就算出了最终基于参数λ的观测序列O的概率分布
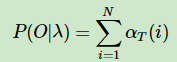
总结:前向算法的思想就是从左往右求出每个时刻的前向概率,这是一种动态规划算法,将每一个时刻与前一时刻前向概率的关系抽象出来,这样就可以轻松的使用迭代表示每一个时刻。然后将所有时刻的前向概率求和,就可以得到最终的概率分布P(O|λ);其中第一时刻的前向概率使用π乘以发射矩阵,后面每一时刻的前向概率使用前一时刻的前向概率乘以状态转移矩阵再乘以发射矩阵。这样我们避免了每一次都遍历序列左右组合的可能性,整个算法的复杂度降为,比暴力求解办法
复杂度有着指数级的下降。
2.后向算法

刚才我们了解了前向算法,其实就是从左往右计算前向概率,然后将每个时刻加起来。所谓的后向算法就是,从右往左计算后向概率,然后将各个时刻加起来。跟前向算法一样,它也是一种动态算法,使用每一时刻和后面时刻状态的关系表示。
前向算法中我们给定t-1时刻前向概率,来计算t时刻的前向概率。前向概率表示的是以隐变量为条件下观测值的概率,那么t时刻的前向概率表示的就是t时刻隐变量为条件下,前面t-1个时刻观测值的概率分布。因为是从前往后推,第一个时刻隐变量的状态π是已知的,所以我们可以直接进行地递推计算。
后向算法跟前向其实正好相反,我们是假设已知t时刻隐变量的条件下,后面t+1到T时刻观测值的概率分布。因为是从后往前面推,所以我们需要先定义一个β,来表示我们刚才的假设。
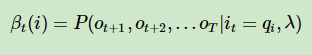
然后我们来表示从t+1时刻到t时刻β的递推关系。对应着上面的图我们可以解释一下,其实很简单的一个逻辑。既然βt+1表示了t+1时刻条件下,后面所有观测值的条件概率分布。那么用βt+1乘以转移矩阵,可以得到βt,乘以发射矩阵B可以得到 t+1时刻观测值的条件概率分布,综合起来得到的βt就可以表示出隐变量t时刻下,t+1和后面所有时刻观测值的条件概率分布。
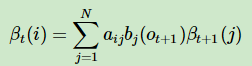
通过递归我们就可以得到第一个时刻隐变量的状态,对应后面所有时刻观测值的条件概率分布。将所有N个状态加起来就得到了λ(初始状态π、转移矩阵、发射矩阵)对应的观测值的概率分布。
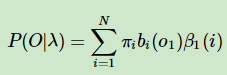
总结:对比着前向算法,我们介绍了后向算法的计算逻辑。其思想和前向算法是一样的,都是通过时刻状态之间的关系来动态表示出参数λ和观测值之间的关系。只不过是因为从右往左推,所以我们需要先定义一个变量β来表示我们的假设。即每一个时刻的隐变量对应后面时刻观测值的概率分布。最终得到第一个时刻π条件下,对应后面观测值的概率分布。所以计算时我们需要初始化t时刻β的值。最终算法复杂度为。
4.维特比(Viterbi)算法
首先维特比算法对应的HMM三个基本问题中的解码问题,即已知模型λ(π,A,B)和观测序列O;需要求出隐藏状态序列S。实际应用比如:语音识别,已知一段语音信息,推测出最有可能对应的文字信息;
不用担心,以我活了这么长时间的经验来讲,往往听名字越是令人恐怖的算法其实才越简单;维特比算法核心思想就是求最优路径,也就是最有可能的隐藏状态序列组合方式;怎么求呢?这其中有一个小技巧,假设你知道了t时刻到t+1时刻的最优路径(最大概率),那么你就能得到t时刻之前的最优路径;继续推一下,假设你知道了倒数第二个时刻到最后时刻的最优路径,那么你就可以推出全局的最优路径了。
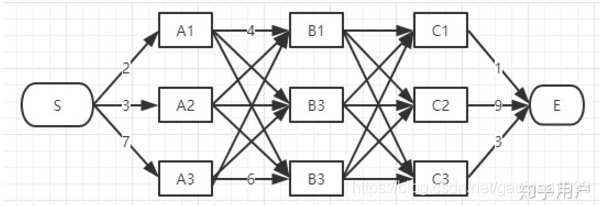
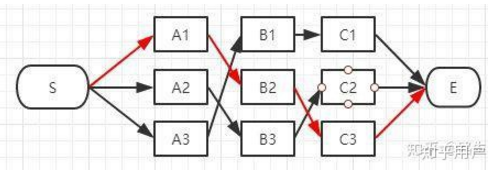
请看上面的两幅图,图一是从S到E的所有可能路径;图二是使用维特比进行处理后的路径,明显更加简单一些。仔细观察会发现,第二幅图之所以简单是因为在每一时刻,对应一个状态只有一条路径。可以将这条路径理解为局部最优路径。最后 到状态E的时候,然后再向后追溯便可以消除其它的路径,只留下一条全局最优路径。
5.总结
本文讲述了隐马尔科夫模型,其是在马尔科夫模型的基础上引入了隐变量,来表达一个序列。并且介绍了马尔可夫三个经典的问题,即学习问题,评估问题,解码问题。最后我们介绍了评估问题的求解方式前向算法和后向算法。后面的学习问题和解码问题,我打算放在下一篇博客中来讲,因为我现在特别想去看电视。
6.废话
我特别喜欢说废话,因为这给我带来健康。我一直都想找一个小孩子,他待在我的身边,安安静静的。我跟他说话的时候,他的回答深邃到使我感到震惊 。他对于其它人都在追求的那些东西没有太大的兴趣,反而是很乐意去干那些别人觉得无聊的事情。他喜欢发呆,喜欢自言自语,喜欢看着远方的天空沉思,好像他不属于这个世界似的。他努力的表现的和大家一样,希望 别人觉得他是一个正常的孩子。只有一个人的时候,他才会觉得幸福。他喜欢跟一些看不见的东西聊天,不是用语言,而是用心。在这个时候,周围的一切好像都是有生命的一样。我走了,而他却始终坐在那个夕阳下的田边,荡着双腿。我说hi,天就要黑了!快点回家去吧!他就跑着回家去,然后躺在妈妈的怀里睡着了。我已经很长时间没有见他了,我想他了,但是我找不到了。
滴答 - 侃侃