隐马尔可夫(HMM)、前/后向算法、Viterbi算法

转自：https://www.cnblogs.com/sddai/p/8475424.html
HMM一直想彻底弄明白，这篇文章较为通俗易懂，留下来多看几遍，其中有我认为公式错误的，进行了相应的修改

HMM的模型

图1

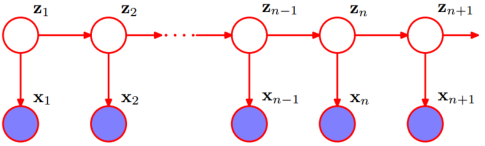
如上图所示，白色那一行描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，蓝紫色那一行是各个状态生成可观测的随机序列

话说，上面也是个贝叶斯网络，而贝叶斯网络中有这么一种，如下图：

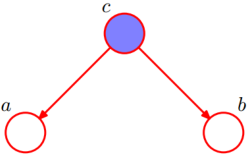
代表：c确定时a和b独立。(c为实心圆代表：c已经被确定)

这时，如果把z1看成a，x1看成b，z2看成c的话，则因为第一个图的z1是不可观测的(所以z1是空心圆)，也就是没确定，则x1和z2就一定有联系。

进一步，如果把z2、x2合在一起看成c的话，则x1和z2、x2就一定有联系，则x1和x2有联系(不独立)。

推广之后：x2和x3不独立，x1和x3也不独立，于是xn们互相不独立。

PS：
LDA假定文章中的词与词之间互相独立，而HMM中是所有的观测互相均不独立。
所以，对于一篇Machine Learn的文章，LDA会吧“机器”和“学习”分成两个词，而HMM会将其视为一个词。

HMM的确定

初始概率分布

z1可能是状态1，状态2 … 状态n，于是z1就有个N点分布：

Z1	状态1	状态2	…	状态n
概率	P1	P2	…	Pn

即：Z1对应个n维的向量。
上面这个n维的向量就是初始概率分布，记做π。

状态转移矩阵

但Z2就不能简单的“同上”完事了，因为Z2和Z1不独立，所以Z2是状态1的概率有：Z1是状态1时Z2是状态1，Z1是状态2时Z2是状态1,…, Z1是状态n时Z2是状态1，于是就是下面的表

$\frac{Z2}{Z1}$	状态1	状态2	…	状态n
状态1	P11	P12	…	P1n
状态2	P21	P22	…	P2n
…	…	…	…	…
状态n	Pn1	Pn2	…	Pnn

即：Z1->Z2对应个n*n的矩阵。
同理：Zi -> Zi+1对应个n*n的矩阵。

上面这些nXn的矩阵被称为状态转移矩阵，用An*n表示。

当然了，真要说的话，Zi -> Zi+1的状态转移矩阵一定都不一样，但在实际应用中一般将这些状态转移矩阵定为同一个，即：只有一个状态转移矩阵。

图1的第一行就搞定了，下面是第二行。

观测矩阵

如果对于zi有：状态1, 状态2, …, 状态n，那zi的每一个状态都会从下面的m个观测中产生一个：观测1, 观测2, …, 观测m，所以有如下矩阵：

$\frac{X}{Z}$	观测1	观测2	…	观测m
状态1	P11	P12	…	P1m
状态2	P21	P22	…	P2m
…	…	…	…	…
状态n	Pn1	Pn2	…	Pnm

这可以用一个n*m的矩阵表示，也就是观测矩阵，记做 $B_{n*m}$。

由于HMM用上面的π，A，B就可以描述了，于是我们就可以说：HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定，为了方便表达，把A, B, π 用 λ 表示，即：
λ = (A, B, π)

例子

假设我们相对如下这行话进行分词：

       欢迎来到我的博客

再假设我们是这样分的：找到“终止字”，然后根据终止字来分词。即：对于这行字，“迎、到、我、的、客”是终止字，于是最终这么分词：欢迎/来到/我/的/博客

下面用上面的知识对这个例子建立HMM的A, B, π：

初始概率分布的确定：

1，对于每个样本，我们的目标是确定其是不是“终止字”，因此对于每个样本，其状态只有n=2个：状态1 – 是、状态2 – 不是。

2，因此初始概率分布π为：

π = {p1，p2}

P1：整个句子中第一个字是非终止字的概率

P2：整个句子中第一个字是终止字的概率

状态转移矩阵的确定：

刚才已经知道状态有n=2个，于是状态转移矩阵就立马得出了，即状态转移矩阵是个n*n的矩阵，如下：

             A=

             p11：非终止字 -> 非终止字的概率。

             p12：非终止字 -> 终止字的概率。

             p21：终止字 -> 非终止字的概率。

              p22：终止字 -> 终止字的概率。

观测矩阵的确定：

如果我们的目标文字使用Unicode编码，那么上面的任何一个字都是0~65535中的一个数，于是我们的观测就会有m=65536个，于是观测矩阵就是个n*m的矩阵，如下：

             B=

             p1,0：Unicode编码中0对应的汉字是非终止字的概率

             p1,65535：Unicode编码中65535对应的汉字是非终止字的概率

             p2,0：Unicode编码中0对应的汉字是终止字的概率

             p2,65535：Unicode编码中65535对应的汉字是终止字的概率

PS：为什么x会有65535个观测啊？“欢迎来到我的博客”这个明明只有8个字。原因是因为真正的HMM面临的情况，即：现有了 Z1=“非终止字”这个状态，然后根据这个状态从65535个字中选出x1=“欢”这个字，然后根据状态转移矩阵，下一次转移到了Z2 =“终止字”，然后根据Z2从65535个字中选出了x2=“迎”这个字，这样，最终生成了这句话。

HMM的两个基本性质

齐次假设

当前状态之和上一个状态有关系，用公式表示的话就是：

P(zt|zt-1,xt-1, zt-2, xt-2, ..., z1, x1)= P(zt | zt-1)

PS：在一开始时说x1和z2、x2不独立，怎么在这里又说x1和x2独立呢？其实真严格追究的话x1和x2的确不互相独立，因为x1是被z1生成的，x2是被z2生成的， 但z2的形成受z1影响，所以x1和x2一定也会有联系，但是为了研究和应用的方便，就假设：生成x1的z1和生成x2的z2不独立，但x1和x2独立。

观测独立性假设

所有的观测之间是互相独立的，某个观测之和生成它的状态有关系，即：

       P(xt|zt,xt, zt-1, xt-1, zt-2, xt-2,..., z1, x1) = P(xt | zt)

PS：在一开始时说x1和z2、x2不独立，怎么在这里又说x1和x2独立呢？其实真严格追究的话x1和x2的确不互相独立，因为x1是被z1生成的，x2是被z2生成的， 但z2的形成受z1影响，所以x1和x2一定也会有联系，但是为了研究和应用的方便，就假设：生成x1的z1和生成x2的z2不独立，但x1和x2独立。

HMM的三个问题

现在有几个问题：

1，知道HMM的参数 λ = (A, B, π) 和观测序列O = {o1,o2, …, oT} ，如何计算模型 λ 下观测序列O出现的概率P(O | λ)。

2，HMM的参数如何确定？

比如：对于刚才的中文分词的小例子。

初始概率分布π好确定：是不是终结词的概率各是0.5。

观测矩阵B也好确定：1/65535嘛

但状态转移矩阵怎么确定？我怎么知道下个词是终结词的概率是多少？

3，知道HMM的参数 λ = (A, B, π) 和观测序列O = {o1,o2, …, oT}，如何计算给定观测序列条件概率P(I|O, λ )最大的状态序列I，即：

对于中文分词，我想到底如何分的词。

上面三个问题：

第一个问题被称为：概率计算问题。
解决办法：前向-后向算法(一种动态规划算法)。

第二个问题被称为：学习问题。
解决办法：如果状态序列已知，那用最大似然估计就好了，但HMM的状态序列未知，即含有隐变量，所以要使用Baum-welch算法(其实其本质就是EM算法)。

第三个问题被称为：预测问题/解码问题。
解决办法：Viterbi算法(一种动态规划算法)。

概率计算问题

该问题有两种解决办法：

1，直接/暴力算法。

2，前向算法/后向算法。

而上面两个算法中的“暴力方法”是实际应用中绝不会被使用的。

Q：那为什么还说这玩意！（踹）

A：理解了直接/暴力算法可以帮助你推导Baum-welch算法。（回踹！）

直接/暴力计算法

问题：已知HMM的参数 λ，和观测序列O = {o1, o2, …,oT}，求P(O|λ)
思想核心：大力出奇迹。
思路：

1，列举所有可能的长度为T的状态序列I = {i1, i2, …, iT}；

2，求各个状态序列I与观测序列 的联合概率P(O,I|λ)；

3，所有可能的状态序列求和∑_I P(O,I|λ)得到P(O|λ)。

步骤：

1，最终目标是求O和I同时出现的联合概率，即：

             P(O,I|λ)= P(O|I, λ)P(I|λ)

那就需要求出P(O|I, λ) 和 P(I|λ)。

2，求P(I|λ) ，即状态序列I = {i1,i2, …, iT} 的概率：

             2.1，P(I|λ) = P(i1,i2, ..., iT |λ)

                  =P(i1 |λ)P(i2, i3, ..., iT |i1, λ)

                  =P(i1 |λ)P(i2 | i1, λ)P(i3, i4, ..., iT |i1, i2 λ)
                  
                   =P(i1 |λ)P(i2 | i1, λ)P(i3 | i1, i2, λ)P(i4, ..., iT |i1, i2, i3, λ)

					=P(i1 |λ)P(i2 | i1, λ)P(i3 | i2, λ)P(i4, ..., iT |i1, i2, i3, λ)  （因为 齐次假设）

                  =......

                  =P(i1 |λ)P(i2 | i1, λ)P(i3 | i2, λ)...P(iT | iT-1, λ)

而上面的P(i1 |λ) 是初始为状态i1的概率，P(i2 | i1, λ) 是从状态i1转移到i2的概率，其他同理，于是分别使用初始概率分布π 和状态转移矩阵A，就得到结果：

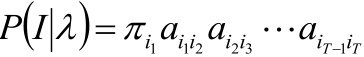
PS：上面的 $a_{i1i2}$代表A的第i1行第i2列。

3，P(O|I, λ)，即对固定的状态序列I，观测序列O的概率是：

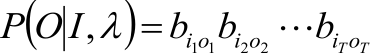
4，代入第一步求出P(O,I|λ)。

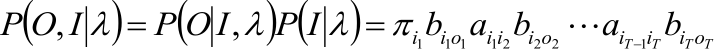
5，对所有可能的状态序列I求和得到观测序列O的概率P(O|λ)：

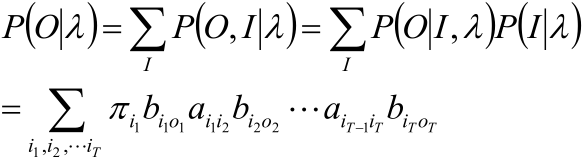
注：上式求和范围（i1,i2,…iT）我觉得表述的不准确，我理解的应该是每个时刻的状态都取遍状态集中所有的状态。
时间复杂度：
每个时刻有n个状态，一共有t个时刻，而根据上面的第5步可以知道每个时刻需要乘2T-1次，所以时间复杂度是： $O((2T-1)n^{T})$

前向算法/后向算法

前向概率-后向概率

如下图所示：

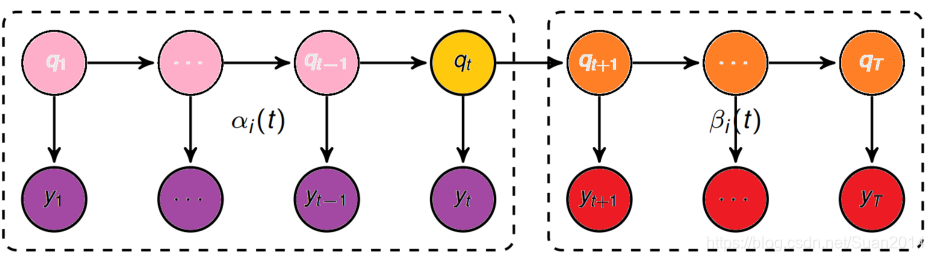
第一行是观测不到的状态序列，第二行是可以观测到的观测序列。

前向概率的定义是：当第t个时刻的状态为i时，前面的时刻分别观测到y1,y2, …, yt的概率，即：

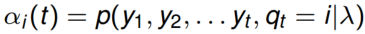
后向概率的定义是：当第t个时刻的状态为i时，后面的时刻分别观测到yt+1,yt+2, …, yT的概率，即：

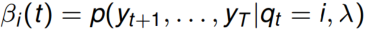
前向算法

如果令前向概率中的t=T，即：

$α_i(T) = p(y1,y2, ..., yT, qT = i | λ)$

那这就意味着，最后一个时刻位于第i号状态时，观测到y1, y2, …, yT的概率，这不就是“直接/暴力计算法”中第4步求出来的P(O,I|λ) 嘛。

因此，如果对 $α_i(T)$ 的i求和，即：

$α_{1}(T) +α_{2}(T) + ...+ α_{n}(T)$ 式1

那就是观测序列O的概率P(O|λ)。

那么如何算 $α_{1}(T) +α_{2}(T) + ...+ α_{n}(T)？$

这样想：

嗯…如果能算出第T-1时刻的前向概率，即 $α_{1}(T-1) +α_{2}(T-1) + ... + α_{n}(T-1)$ 的话，那就能算出式1了(HMM的参数知道了，根据参数不就得了)。

进一步，如果能算出T-2时刻的前向概率，那就能得出T-1时刻的，进而就得出时刻T的了。

按照这个思路：啊！我只要算出1时刻的前向概率不就能算出结果了！

刚才得到了有趣的结果，即：我求出第一个1时刻的前向概率 $α_{i}(1)$ 后就等于求出最终结果了，那 $α_i(1)$ 是啥？

不就是第一个时刻状态为第i号状态时观测到y1的概率吗，即：

$α_{i}(1) = P(y1,q1=i | λ)$

而第一个时刻状态为第i号状态的概率是πi，在第i号状态时得到y1这个观测的概率是Biy1，于是：

$α_i(1) =π_{i}* B_{iy1}$

PS：因为不知道当前是几号状态，所以为了以后的步骤，这里需要将所有的状态都算出来，即：计算出所有的 α1(1) ~ αi(1)

好了，第一个时刻已经求出来了，我们就向后推。

假设现在到第t个时刻了，而第t个时刻的状态是状态j，那我想求时刻t+1状态为i的前向概率怎么求，这样求：

时刻t+1的前向概率的 αi(t+1) 的求法就是：t时刻的状态转移到t+1时刻的状态的概率对所有状态求和 * t时刻的状态得到观测的概率，换句话说就是：t时刻的前向概率对所有的状态求和 * t时刻的状态得到观测的概率。

即：

$a_{i}(t+1) = (∑_j a_{j}(t)a_{ji})b_{iy(t+1)}$

解释一下：

首先，时刻t时状态为j的前向概率是 $a_{j}(t)$。

现在时刻t状态为j的概率知道了，那乘上状态j转移到状态i的转移概率就是时刻t+1时状态为i的概率，即 $a_{j}(t)a_{ji}$ 。

但状态是不可观测的啊，所有我们要计算时刻t时所有状态的情况，于是要对j求和，即： $∑_j a_{j}(t) a_{ji}$，这才是t时刻的状态转移到t+1时刻状态的总概率。

但这样还没完，因为还要由状态得到观测，所以还要在乘上状态i得到观测 $y_{t+1}$的概率，于是就是上面的式子了。

现在 $a_{i}(t+1)$ 知道怎么求了，那不就是所有的的前向概率都知道怎么求了，于是利用刚才的结论：P(O|λ) = α1(T) +α2(T) + … + αn(T)，不就求出观测序列O的概率P(O|λ)了，即：

$P(O|λ) =∑_i α_{i}(T)$

OK，前向算法说完了，下面总结下。

前向算法总结

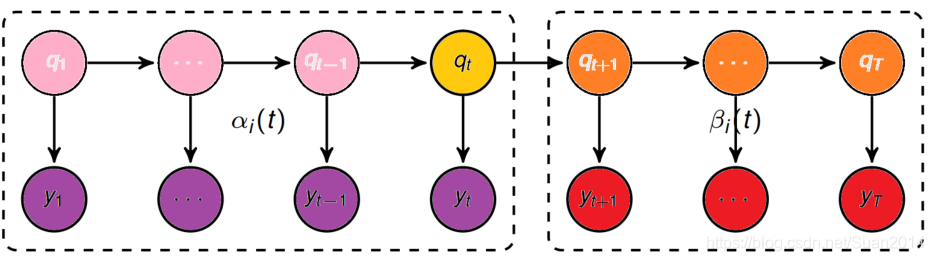
初值： $αi(1) =π_i* B_{iy1}$

递推：对于t = 1, 2, …,T-1

$a_i(t+1) = (∑_j a_j(t)a_{ji})b_{iy(t+1)}$

最终： $P(O|λ) =∑_i α_i(T)$

PS：这里的 αi(t) 中i表示第i号状态，t表示第t时刻。有的教程中会把i和t位置调换一下，变成 αt(i)，其实都一样。

前向算法例子

假设有3个盒子，编号为1,2,3，每个盒子都装有红白两种颜色的小球，数目如下：

盒子号	1	2	3
红球数	5	4	7
白球数	5	6	3

然后按照下面的方法抽取小球，来得到球颜色的观测序列：

1，按照 π=(0.2, 0.4, 0.4) 的概率选择1个盒子，从盒子随机抽出

1个球，记录颜色后放回盒子；

2，按照下图A选择新的盒子，按照下图B抽取球，重复上述过程；

PS：A的第i行是选择到第i号盒子，第j列是转移到j号盒子，如：第一行第二列的0.2代表：上一次选择1号盒子后这次选择2号盒子的概率是0.2。

B的第i行是选择到第i号盒子，第j列是抽取到j号球，如：第二行第一列的0.4代表：选择了2号盒子后抽取红球的概率是0.4。

求：得到观测序列“红白红”的概率是多少？

解：

1，明确已知：HMM模型的参数已经如上图所示了，那我们就需要再明确两件事：HMM中那“看不见的状态”和“可见的观测”分别是什么。

“可见的观测”根据题目可知是：y =“红白红”， “看不见的状态”就是这三次分别选择了什么盒子，且一共有3个状态：选中1号盒子、选中2号盒子、选中3号盒子。

2，根据前向算法，第一步计算 αi(1)，这很简单：

αi =1 (t=1) 即时刻1时位于状态“选中1号盒子”的前向概率，所以：α1(1) =“选中1号盒子”“选中红球” = π0 B10= 0.2*0.5 = 0.1

同理：α2(1) =0.40.4 = 0.16，α3(1) = 0.40.7 = 0.28。

3，计算 αi(2)：

根据公式：

$α_1(2) = (∑_j α_1(2)α_{j1}) b_{1y2}$

$= (0.1*0.5 + 0.16*0.3 + 0.28*0.2) * 0.5$

=0.077

α2(2) = 0.1104

α3(2) = 0.0606

4，同αi(2)，计算αi(3)：

α1(3) =0.04187

α2(3) =0.03551

α3(3) =0.05284

5，最终

$P(O|λ) = ∑_i α_i(3)$

= 0.04187 + 0.03551 + 0.05284

= 0.13022

后向算法

有了前向算法的基础，后向算法就好说了，因为就是前向算法的反过来：先计算最后一个然后推到第一个，于是详细说明就不在给了，直接上结论：

后向算法总结

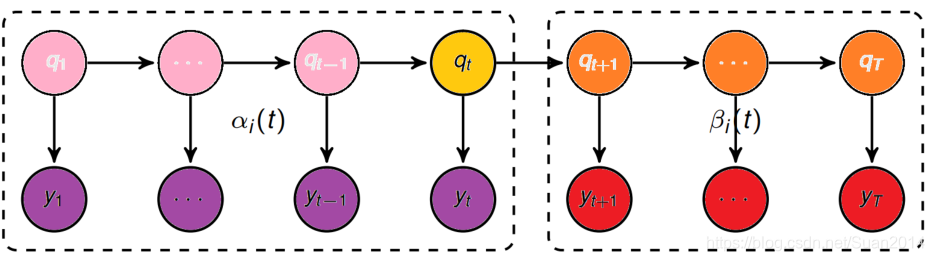
初值： $β_i(T) = 1$

PS：概率为1的原因是 – 本来还需要看看时刻T后面有什么东西，但因为最后一个时刻T 后面已经没有时刻，即不需要再观测某个东西，所以你随便给个什么都行，我不在乎。

递推：对于t = T-1, T-2,…, 1

$β_i(t) = (∑_j a_{ij}b_{jy(t+1)}β_j(t+1))$

PS：这一步是根据t+1的后向概率算t时刻的后向概率βi(t)，因此：

βi(t) = 第t时刻位于第i号状态转移到第t+1时刻位于第j号状态的概率aij * 第t+1时刻第j号状态给出y(t+1) 观测的概率bjy(t+1) * 第t+1时刻的后验概率。

最终： $P(O|λ) =∑_i π_ib_{iy1}β_i(1)$

PS：同第二步，只不过这里是第1时刻。

前后向概率的关系

具体推倒就不给出了，总之：

拥有所有观测时，第t时刻有第i个状态的概率 = t时刻的前向概率 * t时刻的后向概率，即：

$P(i_t = q_i, Y | λ ) = α_i(t) * β_i(t)$

单个状态的概率

这里的单个状态是什么呢？就是给定观测O和HMM的参数 λ 时，在时刻t时位于隐状态i的概率，记为：

$γ_t(i) = P(i_t= q_i | O, λ)$

PS：这里的O是所有观测的合集，即：O = {y1 = o1, y2 = o2, …,yT = oT}

这个就很强啦，因为我们可以估计在t时刻的隐状态，进而求出隐状态序列！

PS：这个的确是求隐状态序列的一种方式，但这种有个问题 – 求出的隐状态之间互相独立，即：没有考虑到第t+1时刻的隐状态是由第t时刻的隐状态转移过来的情况。换言之：这样求得的隐状态是“每个隐状态都是仅在当前时刻最优，可每个隐状态都没考虑到全局情况”。

而它的求解也很简单，如下：

两个状态的联合概率

刚才“单个状态的概率”求得的t时刻的隐状态没有考虑到“上下文”，那就考虑下上下文，即：时刻t位于隐状态i时，t+1时刻位于隐状态j，记为：

$ξ_t(i, j) =P(i_t = q_i, i_{t+1} = q_j | O, λ)$

求解推导：

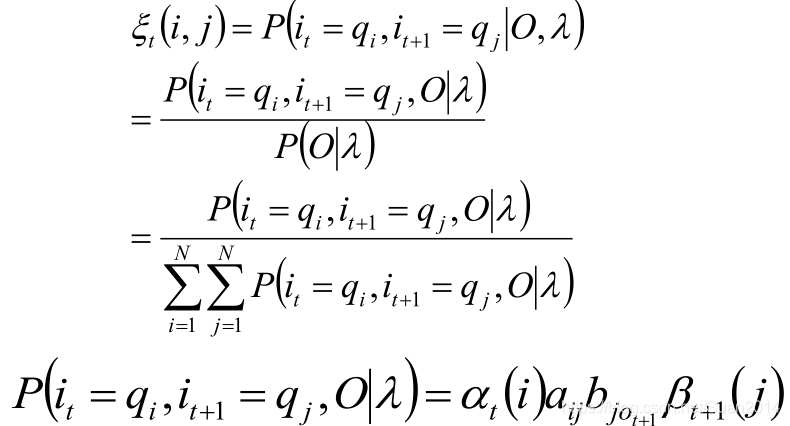
一些期望

学习问题

学习问题分两种：

1， 观测序列和隐状态序列都给出，求HMM。

PS：这种学习是监督学习。

2， 给出观测序列，但没给出隐状态序列，求HMM。

PS：这种学习是非监督学习，利用Baum-Welch算法。

观测序列和隐状态序列都给出

这种其实求法超简单：用大数定理用频率来估算HMM的三种概率就OK了。

解释：

还是用最开始的分词的例子。

初始概率：

i = 0：第一个文字是终止字的次数 / (第一个文字是终止字的次数 + 不是终止字的次数)

i = 1：第一个文字不是终止字的次数 / (第一个文字是终止字的次数 + 不是终止字的次数)

转移概率：

i=0,j=0：第t个字是终止字，第t+1个字是终止字的次数 / (第t个字是终止字，第t+1个字是终止字的次数 + 第t个字是终止字，第t+1个字不是终止字的次数 + 第t个字不是终止字，第t+1个字是终止字的次数 + 第t个字不是终止字，第t+1个字不是终止字的次数)

i=0,j=1、i=1, j=0、i=1, j=1同理。

观测概率：

i=0,k=0：Unicode编码中编码为0的字是终止字的次数 / (Unicode编码中编码为0的字是终止字的次数 + Unicode编码中编码为0的字不是终止字的次数)

i=1,k=0：Unicode编码中编码为0的字不是终止字的次数 / (Unicode编码中编码为0的字是终止字的次数 + Unicode编码中编码为0的字不是终止字的次数)

其他k=j同理。

Baum-Welch算法

其实该算法的本质就是EM算法，因为它解决的问题就是：有了观测值X，而观测值有个隐变量Z时，求在HMM参数 λ下的联合概率P(X, Z | λ) 。

PS：我总结的EM算法地址如下：

http://blog.csdn.net/xueyingxue001/article/details/52020673

这里在贴一下EM算法的步骤：

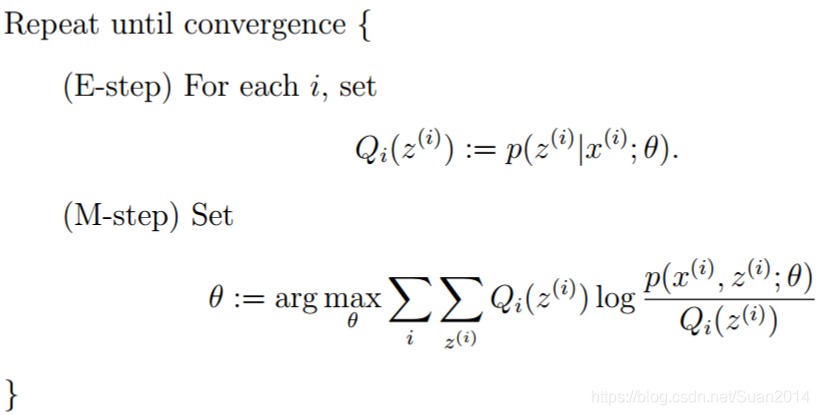
上面的步骤写成统一的式子就是：

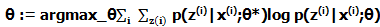
因此EM算法对应到HMM的学习问题就是：

所有观测数据写成O=(o1, o2 …oT)，所有隐数据写成I=(i1, i2 …iT)，完全数据是(O, I)=(o1, o2 …oT ,i1,i2 … iT)，完全数据的对数似然函数是lnP(O, I | λ)

于是：

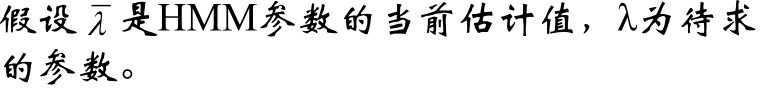
就有如下推导：

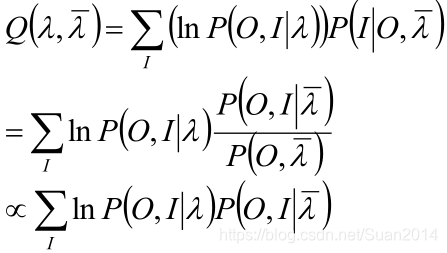
解释：

第一行：EM的Q函数。

第二行：条件概率公式。

第三行：

第一：第二行分母代表“上一次求出的参数与观测集合的联合概率”，对本次的估计没帮助，所以可以舍去。

第二：第三行那个是正比符号，即使没有上一个解释可是可以保证第二行与第三行是成正比的。

话说，P(O, I | λ) 在“HMM概率计算问题”的“直接/暴力计算法”中已经解出了，这里再贴下截图：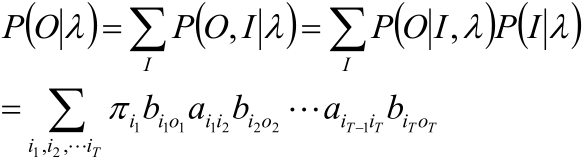
于是上面可以进一步做如下推导：

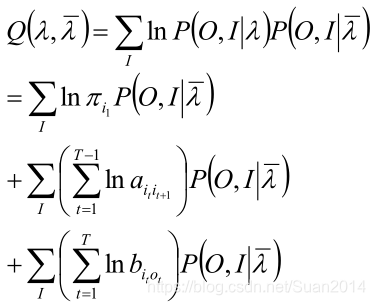
对于上式，除了HMM的参数 λ = (A, B, π) 外都是已知的了。

话说上图将最后一个等号写在3行是为了表述一点：这三行的每一行仅包含HMM的一个参数，而我们的目标是求Q函数的最大，于是只要求最后三行的最大就好了。为了方便说明，我将上图最后三行的三个式子从上向下依次命名为：π式，α式，β式。

求 π 式

π 式有个约束：所有πi的和为1。

于是对于有约束的求极值为题就拉格朗日乘子法的伺候！

1，拉格朗日函数

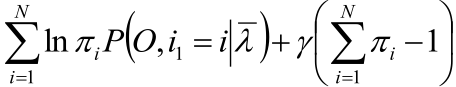
2，上式对 πi 求偏导

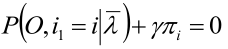
3，上式对i求和后 πi 的和为1就把 π 约掉了，从而求出拉格朗日参数

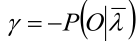
4，将上式带入第二步的式子就求出了π：

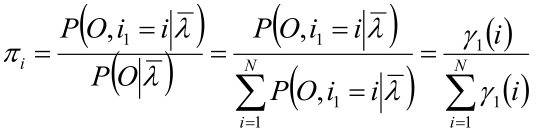
而上式的 γ 就是“HMM概率计算问题”中“单个状态的概率”中的 γ(PS：不是拉格朗日参数)，于是 π 就求出来了！

求 α 式

α 式可以写成

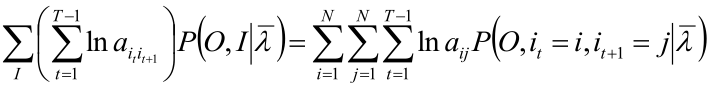
仍然使用拉格朗日乘子法，得到

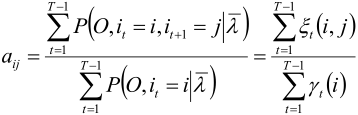
上式的 γ 是“HMM概率计算问题”中“单个状态的概率”中的 γ，上式的 ξ 是“HMM概率计算问题”中“两个状态的联合概率”中的 ξ。

求 β 式

同理，得到：

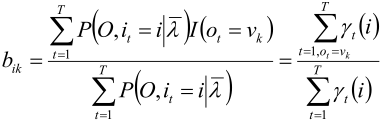
上式的 γ 是“HMM概率计算问题”中“单个状态的概率”中的 γ。

预测问题

预测问题有两种解决办法：

1， 近似算法。其实就是“HMM概率计算问题”中“单个状态的概率”的解法。

2， Viterbi 算法。下面讲解这个。

VIterbi算法

在介绍维特比算法之前，我先用通俗的语言描述下它。

假设我们遇到了这么个问题：

大学时你让室友帮你带饭(如果你上过大学，别告诉我你没干过这事…)，然后你室友问你想吃啥？你回答：“你吃啥我吃啥，不过回来时帮忙带瓶雪碧，谢啦”。于是有趣的事就发生了：你室友给你带回了饭和雪碧并兴高采烈的说：“我去，食堂换大厨了，那个小卖部的收银员换成了个漂亮妹子！！”然后你问他：“你去的哪个食堂和小卖部？”，他想了想回答：“你猜。”

好了，你猜吧~

我猜你妹啊(╯‵□′)╯︵┻━┻

嘛，先别慌掀桌，不管如何你室友帮你带了饭，所以咱们就满足下他那小小的恶作剧，就当做是给他跑腿的辛苦费好了。

PS：假设你学校有2个小卖部和2个食堂。

于是，mission start！

首先，问他：你先去得小卖部？他回答：是的。

OK，买东西的先后顺序搞定了，如下图：

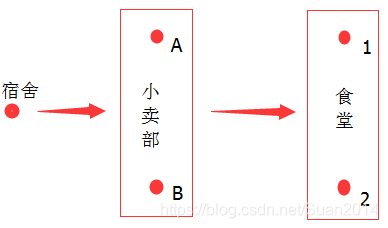
接下来开始思考：

第一步：从宿舍到小卖部A和B的距离都差不多，不好判断，即从宿舍到小卖部A的概率 = 从宿舍到小卖部B的概率，如下图；

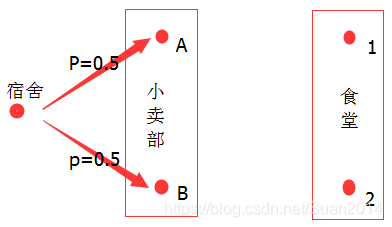
第二步：从小卖部A、B到食堂1、2有四种路线(A1, A2, B1, B2)，然后这四种路线中到食堂1最短的是A1，到食堂2最短的是B2，然后这货绝对那个近选哪个，所以如果去食堂1，则他会选择A1，如果去食堂2，则他会选择B2，如下图：

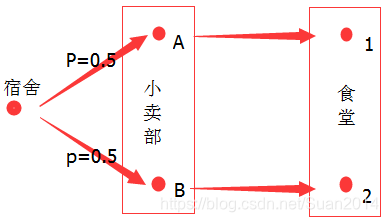
第三步：看看他给带来的饭，嗯…这个饭我记得食堂1有卖，食堂2不知道，就当没有吧，那就假设他去的是食堂1，如下图：

第四步：OK，终点已经确定，接下来反推回去，就好了，即：他绝壁选个最近的小卖部，所以他会选择距离食堂1最近的小卖部A，如下图：

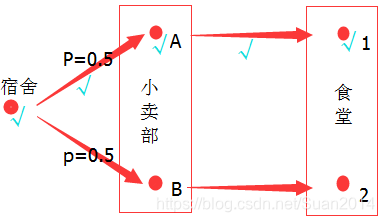
第五步：对他说：“你先去小卖部A然后去食堂1对吧”，他说：“我次奥，你咋知道的”。

OK，例子举完了，我们来看看维特比算法，其实维特比算法就是上面的过程： 1，先从前向后推出一步步路径的最大可能，最终会得到一个从起点连接每一个终点的m条路径(假设有m个终点)。

2，确定终点之后在反过来选择前面的路径。

3，确定最优路径。

下面看看Viterbi算法的定义。

Viterbi 算法的定义

定义变量δt(i)：表示时刻t状态为i的所有路径中的概率最大值，公式如下：

过程：

上面的符号之前都已经见过，这里不再解释，下面为了更好地理解这几步，我们来举个例子。

例子

还是盒子球模型。

盒子和球模型λ= (A, B,π)，状态集合Q={1, 2, 3}，观测集合V={红, 白}，

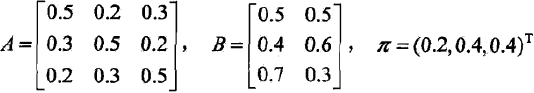
已知观测序列O=(红，白，红)，试求最优状态序列，即最优路径I*= (i1*, i2*, i3*)。

解：

如下图所示(图中的数字在之后的步骤中会一一推导出来)

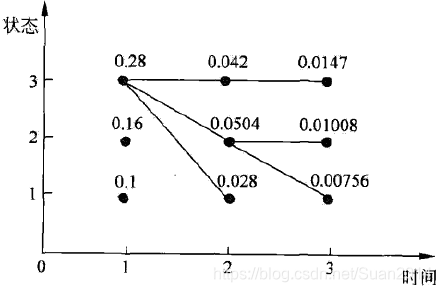
要在所有可能的路径中选择一条最优路径，按照以下步骤出来。

1，初始化

t=1时，对每个状态i, i=1, 2, 3，求状态为i观测o1为红的概率，记此概率为δ1(i)，则：

$δ_1(i) = π_ib_i(o1)=π_ib_i(红)$， i = 1, 2, 3

代入实际数据

δ1(1) = 0.10，δ1(2) =0.16，δ1(3) = 0.28

记ψ1(i) = 0，i = 1, 2, 3。

2，在t=n时

t=2时，对每个状态i，求在t=1时状态为j观测为红并且在t=2时状态为i观测为白的路径的最大概率，记概率为δ2(t)，则根据：

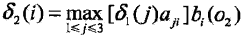
同时，对每个状态i, i = 1, 2, 3，记录概率最大路径的前一个状态j：

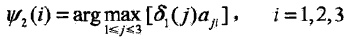
计算：

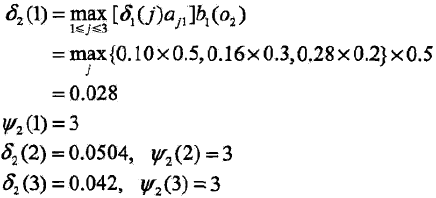
同样，在t=3时

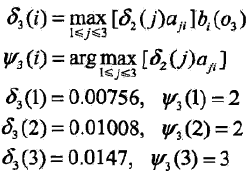
3，求最优路径的终点

以P*表示最优路径的概率，则

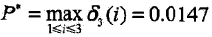
最优路径的终点是 $i_3^*$:

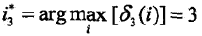
4，逆向找 $i_2^*$, $i_1^*$：
在t=2时， $i_2^* = ψ_3(i_3^*) =ψ_3(3) = 3$

在t=2时， $i_1^* = ψ_2(i_2^*) =ψ_2(3) = 3$

于是求得最优路径，即最有状态序列 $I* = (i_1^*,i_2^*, i_3^*) = (3, 3, 3)$。