机器学习 - 隐马尔科夫模型（2）- 前向 and 后向算法

前向算法

前向概率
观测序列概率的前向算法
例子

后向算法

后向概率
观测序列概率的后向算法
例子

前向算法

前向算法可以理解成我们之前接触的 Adaboost 算法中的前向分步算法，即后一时刻（t+1）某观测值出现概率的计算，依靠当前时刻（t）的概率。这样我们省去了在直接计算法中的重复计算过程，因为我们 保存了 在时刻 t 时各观测值出现的概率；而直接计算方法中，每种情况的计算都需要 从头至尾 全部重新计算。

前向概率

给定模型 $λ$ ，定义截止到时刻 t 部分的观测序列为 $o_1,o_2,…,o_t$ ，且状态为 $q_n$ 的概率为前向概率，记作：

$α_t(s)=P(o_1,o_2,…,o_t，s_t=q_n|λ)=P(o_1，s_t=q_n|λ)·P(o_2，s_t=q_n|λ)·…·P(o_t，s_t=q_n|λ)$

以此我们可以递推地计算前向概率，最终求得观测序列概率 $P(O|λ)$ 。
观测序列概率的前向算法

$\bullet$ 计算初值。在 t=1 时刻，计算在不同状态下，出现观测值 $o_1$ 的概率：

$α_1(s)=π_sb_s(o_1)，s=q_1,q_2,...,q_N$

$\bullet$ 递推计算。以此对 t=2,3,…,T，依据前一时刻的计算结果，计算转移到下一个状态的情况下，出现观测值 $o_t$ 的概率：

$α_t(s)=[\sum_{j=q_1}^{q_N}α_{t-1}(j)α_{js}]b_s(o_t)，s=q_1,q_2,...,q_N$

$\bullet$ 计算完毕。 $P(O|λ)=\sum_{s=q_1}^{q_N}α_T(s)$

例子

沿用上一篇文章的例子：

假设有 4 个盒子，每个盒子都装有红白两种颜色的球，各盒子的红白球数为：

盒子编号	1	2	3	4
红球数	5	3	6	8
白球数	5	7	4	2

我们按照以下方法抽取小球并产生颜色的观测序列：

开始时，从 4 个盒子中 等概率 随机选取一个盒子，从盒子中抽取 1 个小球记录颜色并放回；

且 状态转移概率矩阵为： $A=\begin{bmatrix} 0 & 1 & 0 & 0\\ 0.4 & 0 & 0.6 & 0\\ 0 & 0.4 & 0 & 0.6\\ 0 & 0 & 0.5 & 0.5\\ \end{bmatrix} \quad$

图模型表示：
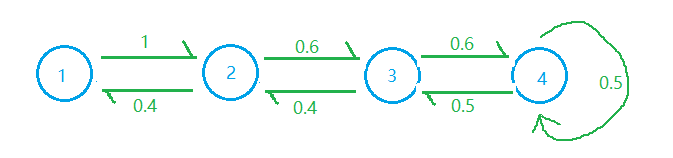
状态转移概率图模型
观测概率矩阵 为： $B=\begin{bmatrix} 0.5 & 0.5\\ 0.3 & 0.7\\ 0.6 & 0.4\\ 0.8 & 0.2\\ \end{bmatrix} \quad$

假设已知观测序列为： $O=(红，白)$

那么使用前向算法计算：

在 t=1 时刻：

$\begin{cases} α_1(1)=π_1b_1(o_1)=0.25*0.5=0.125\\ α_1(2)=π_2b_2(o_1)=0.25*0.3=0.75\\ α_1(3)=π_3b_3(o_1)=0.25*0.6=0.15\\ α_1(4)=π_4b_4(o_1)=0.25*0.8=0.2\\ \end{cases}$

在 t=2 时刻：

$\begin{cases} α_2(1)=[\sum_{i=1}^{4}α_{(i1)}a_{i1}]·b_1(o_2)=[0+0.125+0+0]*0.5=0.0625\\ α_2(2)=[\sum_{i=1}^{4}α_{(i2)}a_{i2}]·b_2(o_2)=[0.3+0+0.45+0]*0.7=0.525\\ α_2(3)=[\sum_{i=1}^{4}α_{(i3)}a_{i3}]·b_3(o_2)=[0+0.06+0+0.09]*0.4=0.06\\ α_2(4)=[\sum_{i=1}^{4}α_{(i4)}a_{i4}]·b_4(o_2)=[0+0+0.1+0.1]*0.2=0.04\\ \end{cases}$

最终 $P(O|λ)=0.0625+0.525+0.06+0.04=0.6875$

所以，该模型 $λ$ 产生观测序列 $O=(红，白)$ 的概率为 0.6875

后向算法

前向概率的计算为从前至后逐时刻计算当前时刻的所有概率，并为后续概率计算留存结果。而后向概率则是从后向前，逐时刻递减的计算，实际上大同小异。
1. 后向概率
  
  给定隐马尔科夫模型 $λ$ ，定义在时刻 t 状态为 $q_i$ 的条件下，从 t+1 时刻到 T 时刻的部分观测序列为 $o_{t+1},o_{t+2},...,o_T$ 的概率为后向概率，记作：
  
  $β_t(s)=P(o_{t+1},o_{t+2},…,o_T|s_t=q_n,λ)=P(o_{t+1}|s_t=q_n,λ)·P(o_{t+2}|s_t=q_n,λ)·…·P(o_t|s_t=q_n,λ)$
  
  同样可以使用递推的方法计算后向概率，最终求得观测序列概率 $P(O|λ)$
2. 观测序列概率的后向算法
  
  $\bullet$ 初始概率。定义最后时刻的概率为 1.
  
  $β_T(s)=1，s=q_1,q_2,...,q_N$
  
  $\bullet$ 对 t=T-1,T-2,…,1，根据后一时刻的概率，逐步计算当前时刻的概率。即根据当前时刻的结果概率，估计前一时刻可以产生此结果的不同状态的概率。
  
  $β_t(s)=\sum_{j=q_1}^{q_N}a_{sj}b_s(o_{t+1})β_{t+1}(s)，s=q_1,q_2,...,q_N$
  
  $\bullet$ 计算完毕。最终 $P(O|λ)=\sum_{s=q_1}^{q_N}π_sb_s(o_1)β_1(s)$
3. 例子
  
  沿用上例：
  
  在 t=2 时：
  
  $\begin{cases} β_2(1)=1\\ β_2(2)=1\\ β_2(3)=1\\ β_2(4)=1\\ \end{cases}$
  
  在 t=1 时：
  
  $\begin{cases} β_1(1)=\sum_{i=1}^{4}a_{1i}b_i(o_2)β_2(i)=0+0.5+0+0=0.5\\ β_1(2)=\sum_{i=1}^{4}a_{2i}b_i(o_2)β_2(i)=0.4*0.7+0+0.6*0.4+0=0.52\\ β_1(3)=\sum_{i=1}^{4}a_{3i}b_i(o_2)β_2(i)=0+0.4*0.4+0+0.6*0.2=0.28\\ β_1(4)=\sum_{i=1}^{4}a_{4i}b_i(o_2)β_2(i)=0+0+0.5*0.4+0.5*0.2=0.3\\ \end{cases}$
  
  在初始时，得到最终概率：
  
  $P(O|λ)=\sum_{i=1}^{4}π_ib_i(o_1)β_1(i)=0.25*(0.5*0.5+0.3*0.52+0.6*0.28+0.8*0.3)=0.2035$