从零开始-Machine Learning学习笔记(32)-强化学习

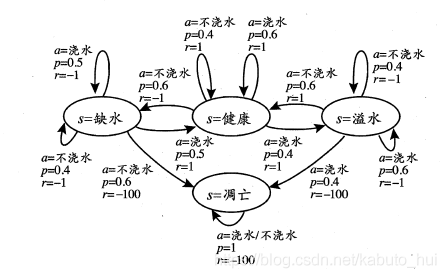
在上面的这个图中，状态空间一共有四种情况X={缺水，健康，溢水，凋亡}，当处于“缺水”的状态的时候；如果执行动作“浇水”，则有p=0.5的概率状态会转移到“缺水”，还有p=0.5的概率状态会转移到“健康”；当状态从“缺水”转移到“缺水”的时候，给出的奖赏是-1，当状态从“缺水”转移到“健康”的时候，给出的奖赏为1。同理，如果执行的动作是“不浇水”，则有p=0.4的概率状态会转移到“缺水”，还有p=0.6的概率状态会转移到“凋亡”；当状态从“缺水”转移到“缺水”的时候，给出的奖赏是-1，当状态从“缺水”转移到“凋亡”的时候，给出的奖赏-100。

机器要做的是通过在环境中不断地尝试而学得一个"策略"(policy) $\pi$ ，根据这个策略，在状态z 下就能得知要执行的动作 $a = \pi (x)$ ，例如看到瓜苗状态是缺水时，能返回动作"浇水"。于是使用 $\pi(x,a)$ 表示状态为x下选择动作为a的概率，这里有 $\sum_{a}\pi(x,a)=1$ 。

策略的优劣取决于长期执行这一策略后得到的累积奖赏；所以强化学习就是要学习出一种策略，使得最后的累计奖赏最高。

1. K-摇臂赌博机

强化学习任务的最终奖赏是在多步动作之后才能观察到，这里我们不妨先考虑比较简单的情形:最大化单步奖赏，即仅考虑一步操作。最大化单步奖赏需要考虑两个方面：（1）每个动作的奖赏；（2）要执行奖赏最大的动作。
如果每个动作的奖赏是一个确定的值，那么遍历所有的奖赏就能找到最大的动作；但是更多的时候，一个动作的奖赏值往往来自于一个概率分布，所以，一次尝试并不能确切地获得平均奖赏值。

1.1 探索与利用

单步强化学习任务就对应了一个理论模型-“K-摇臂赌博机”。所谓的K-摇臂赌博机是有k个摇臂，投入一个硬币后可以按下一个摇臂，每个摇臂以一定的概率吐出硬币，但是这个概率是多少并不知道。于是赌徒需要通过一定的策略使得自己获得最多的硬币，即最大化奖赏！于是就有以下的两种策略：
仅探索(exploration-only)：将所有机会平均分配给每个摇臂，最后用每个摇臂各自的平均吐币概率作为作为其奖赏期望的近似估计；
仅利用(exploitation-only)：选择到目前为止平均奖赏最大的摇臂，若有几个摇臂的平均奖赏一样的大，则随机选择一个。

仅探索可以很好的估计每个摇臂的奖赏，但是却失去了很多选择最大奖赏的机会；仅利用则没有估计每个摇臂的奖赏，很可能选不到奖赏最大的摇臂。这两种情况的感觉就好像是：
仅探索说我知道那个给的奖赏多，但我没有多少选择的机会了，我大部分的机会都是用于试出奖赏最大的摇臂；而仅利用说我不知道哪个摇臂给的奖赏最多，我就一直选我当前所知道的给的奖赏最多的那个摇臂，要是我提前知道那个最多，我就一直选择那个最大，这样我的奖赏就是最大的！

所以这两种情况是矛盾的，欲使累积的奖赏最大，就需要在“仅探索”和“仅利用”之间达到一个平衡！

1.2 $\epsilon$ -贪心

$\epsilon$ 贪心法是用一个概率来将探索和利用进行了一个折中。每次尝试时，以 $\epsilon$ 的概率进行探索，即以均匀概率随机选取一个摇臂;以 $1 - \epsilon$ 的概率进行利用，即选择当前平均奖赏最高的摇臂(若有多个，则随机选取一个)。
令Q(k)来记录摇臂k的平均奖赏，假设摇臂k被尝试了n次，每次的奖赏为 $v_i$ ，于是有：
$Q_n(k) = \frac{1}{n} \sum_{i=1}^{n}v_i \\ =\frac{1}{n} (v_1+v_2+...+v_{n-1}+v_n) \\ =\frac{1}{n}[ (n-1)\frac{1}{n-1}(v_1+v_2+...+v_{n-1})+v_n] \\ =\frac{1}{n}[ (n-1)Q_{n-1}(k)+v_n]$
于是每次只需要记录已尝试的次数n和最近的平均奖赏 $Q_{n-1}(k)$ 即可计算当前的平均奖赏，其算法描述如下所示：

1.3 Softmax

Softmax算法基于当前已知的摇臂平均奖赏来对探索和利用进行折中。若各摇臂的平均奖赏相当，则选取各摇臂的概率也相当;若某些摇臂的平均奖赏
明显高于其他摇臂，则它们被选取的概率也明显更高。所以区别于 $\epsilon$ -贪心，Softmax通过控制摇臂k被选中的概率，来对探索和利用进行折中，Softmax使用了一个Boltzmann分布：
$P(k) = \frac{e^{\frac{Q(k)}{\tau}}}{\sum_{i=1}^{k}e^{\frac{Q(k)}{\tau}}}$
其中 $\tau > 0$ 称为温度，其值越小，则平均累计奖赏高的摇臂被选取的概率越高。 $\tau$ 趋近于0，Softmax则趋近于仅利用，因为每次取出的都是当前平均累计奖赏最高的样本； $\tau$ 趋近与无穷大，Softmax趋近于仅探索，因为P(k)接近于1/K，是一个均匀分布，选择哪一个摇臂的概率都一样。

2. 有模型学习

上一小节的K-摇臂赌博机是一种单步强化学习任务。如果我们要考虑多步强化学习任务，暂且先假定任务对应的马尔可夫决策过程四元组 $E= (X， A ， P， R)$ 均为己知，这样的情形称为"模型己知"，即机器已对环境进行了建模，能在机器内部模拟出与环境相同或近似的状况。在己知模型的环境中学习称为"有模型学习"(model-based learning)。

2.1 策略评估

在模型己知时，对任意策略 $\pi$ 能估计出该策略带来的期望累积奖赏。下面做几个约定：
$V^{\pi}(x)$ ：表示从状态x出发，使用策略 $\pi$ 所带来的累计奖赏；
$Q^{\pi}(x,a)$ ：表示从状态x出发，执行动作a后再使用策略所带来的累计奖赏；
$V(·)$ ：被称为状态值函数(state value function)，表示在指定状态上的累积奖赏； $Q(·)$ ：被称为状态-动作值函数(state-action value function)，表示指定在状态-动作上的累积奖赏。根据累计函数的定义，我们可以写出状态值函数和状态动作值函数：

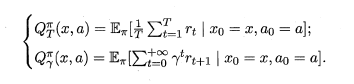
需要注意的是，上式中的 $P_{x→x'}^a$ 表示在执行动作a后，由状态x转移到状态x’的概率，这个概率乘以这个时候奖赏： $(R_{x→x'}^a + \gamma V_{\gamma}^{\pi}(x'))$ ，在对所有的动作a和状态x求和，得到就是期望，也就是我们式子中的值函数展开。于是基于T步累积奖赏的策略评估算法：

其中第三行的退出条件也可以设置为：
$\max_{x∈X} |V(x)-V^{'}(x)| < \theta$
有了状态值函数，就可以估算状态-动作值函数：

2.2 策略改进

对某个策略的累积奖赏进行评估后，若发现它并非最优策略，则当然活望对其进行改进。理想的策略应能最大化累积奖赏：
$\pi^* = \arg \max_{\pi}\sum_{x∈X}V^{\pi}(x)$
最优策略所对应的值函数称为最优值函数，由于最优值函数的累积奖赏值已经是最大，可对前面的值函数的展开式做一个改动：将对动作的求和改为取最优

于是对于当前策略，可以修改为：
$\pi^{'}(x)=\arg \max_{a∈A}Q^{\pi}(x,a)$
直到 $\pi$ 和 $\pi^{'}$ 一致、不再发生变化时，就找到了最优策略。

2.3 策略迭代与值迭代

在前面的两个小结中，我们知道了如何去评估一个策略的值函数，也知道怎么去改进这个策略达到最优策略。所以这一小节主要将如何将这两部分结合起来得到求最优解的方法：从一个初始策略(通常是随机策略)出发，先进行策略评估，然后改进策略，评估改进的策略，再进一步改进策略，……不断迭代进行策略评估和改进，直到策略收敛、不再改变为止.这样的做法称为"策略迭代" (policy iteration)。
以下是基于T步累积奖赏的策略迭代算法：

这个时候，我们将每次迭代过程中值函数的求解换成最优值函数，迭代完成之后，最后计算状态-动作函数，最后对于每个状态选择能使该状态对应的状态-动作函数最大的动作作为该状态的策略，于是就得到了的值迭代算法：

3. 免模型学习

在现实的强化学习任务中，环境的转移概率、奖赏函数往往很难得知，甚至很难知道环境中一共有多少状态。若学习算法不依赖于环境建模，则称为"免模型学习" (model-free learning)，这比有模型学习要困难得多。

3.1 蒙特卡罗强化学习

蒙特卡洛强化学习对应于有模型学习中策略评估。因为模型未知，所以无法进行全概率展开，也就无法进行策略估计。所以这里采用的方法是：多次采样，然后取平均累计奖赏来作为期望累积奖赏的近似。 这种方法称之为蒙特卡罗强化学习。
在模型未知的情形下，我们从起始状态出发、使用某种策略进行采样，执行该策略T步并获得轨迹，然后，对轨迹中出现的每一对状态-动作，记录其后的奖赏之和，作为该状态-动作对的一次累积奖赏采样值。多次来样得到多条轨迹后 ，将每个状态-动作对的累积奖赏采样值进行平均，即得到状态-动作值函数的估计。
因为要多次采样以获得多条轨迹，所谓每次的策略不能是确定的。于是基于 $\epsilon$ -贪心启发，我们选择策略也可以基于 $\epsilon$ -贪心：

其中 $\pi (x)$ 称为原始策略，其实也就是状态x对应的一个动作a，但是在这个状态中，可能有很多种动作a可供选择，于是我们让这个 $\epsilon$ -贪心策略也以概率 $\epsilon$ 能够随机均匀的取到所有的动作a。在使用策略评估之后，我们还需要对策略进行改进，这个时候只需要讲上面式子中的 $\pi (x)$ 替换为： $\arg \max_{a'}Q(x,a')$ ，用当前最大状态-动作函数所对应的最大动作a来替换原来的策略。因为策略评估与改进使用的都是同一个策略，因此被称为“同策略蒙特卡罗强化学习算法”：

使用策略 $\pi$ 的采样轨迹来评估策略 $\pi$ ，实际上就是对累计奖赏函数估计期望：
$Q(x,a)=\frac{1}{m} \sum_{i=1}^{m}r_i$
如果使用策略 $\pi ^{'}$ 的采样轨迹来估计策略 $\pi$ ，则只需要对累计奖赏行数进行加权：
$Q(x,a)=\frac{1}{m} \sum_{i=1}^{m} \frac{P_i^{\pi}}{P_i^{\pi ^{'}}}r_i$
其中， $P_i^{\pi}$ 是策略 $\pi$ 产生第i条轨迹的概率； $P_i^{\pi^{'}}$ 是策略 $\pi^{'}$ 产生第i条轨迹的概率；如果给定一条轨迹，那么策略 $\pi$ 产生这条轨迹的概率为：
$P^{\pi}=\prod_{i=0}^{T-1}\pi(x_i,a_i)P_{x_i→x_{i+1}}^{a_i}$
把这个式子带入到加权累积奖赏函数Q中，就可以发现，Q的计算跟环境的状态转移概率 $P_{x_i→x_{i+1}}^{a_i}$ 无关：
$Q(x,a) = \frac{1}{m} \sum_{i=1}^{m}\ \prod_{i=1}^{T-1}\frac{\pi(x_i,a_i)}{\pi{'}(x_i,a_i)}r_i \\ 其中策略\pi是确定性的策略，而\pi^{'}是\epsilon -贪心的：\\ Q(x,a) = \frac{1}{m} \sum_{i=1}^{m}\ \prod_{i=1}^{T-1}\frac{1}{p_i}r_i \\ 其中：\pi(x_i,a_i) = 1 \\ \pi{'}(x_i,a_i)=p_i = \begin{cases} 1-\epsilon+\frac{\epsilon}{|A|}, & \text{$a_i=\pi(x)$} \\ \frac{\epsilon}{|A|}, & \text{$a_i \neq \pi(x)$} \end{cases}$
于是，因为策略评估与策略更新用的不是一个策略，所以下面的这个算法也叫做“异策略蒙特卡罗强化学习算法”：

3.2 时序差分学习

时序差分(Temporal Difference, TD)学习则结合了动态规划与蒙特卡罗方法的思想，能做到更高效的免模型学习。
还记得之前关于Q的增量式计算为：
$Q_{t+1}^{\pi}(x,a) = Q_{t}^{\pi}(x,a)+\frac{1}{t+1}(r_{t+1}-Q_t^{\pi}(x,a)) \\ 把\frac{1}{t+1}替换为\alpha，于是：\\ Q_{t+1}^{\pi}(x,a) = Q_{t}^{\pi}(x,a)+\alpha(r_{t+1}-Q_t^{\pi}(x,a)) \\$
以 $\gamma$ 折扣累积奖赏为例：

使用上面的这个式子，每执行一步策略就更新一次函数估计，这就是Sarsa算法，因为每次更新函数值都需要知道前一步的状态(State)、动作(Action)、奖赏值(Reward)和当前状态(State)、将要执行的动作(Action)，因为Sarsa算法还是对同一个策略进行评估和改进，所是一个同策略的算法：

如果进行策略评估的时候使用贪心策略，而策略改进的时候使用的是原始策略，这样使用不同的策略进行改进和评估，就得到了异策略算法-Q学习算法：

4. 值函数近似

之前的学习都是假定强化学习任务的状态x是有限的。而现实的强化学习任务所面临的状态空间往往是连续的，有无穷多个状态。所以，我们可以对连续状态空间的值函数进行学习。先考虑简单情形，即值函数能表达为状态的线性函数：
$V_{\theta}(x) = \theta^T x$
其中x为状态向量， $\theta$ 为参数向量。由于此时的值函数难以像有限状态那
样精确记录每个状态的值，因此这样值函数的求解被称为值函数近似(Value Function Approximation)。我们对学得的值函数使用最小二乘误差来度量，然后使用梯度下降就可以求得 $\theta$ 的更新规则：

由于我们并不知道策略的真实值函数，但是我们可以借助时序差分学习，基于 $V^{\pi}(x)=r+\gamma V^{\pi}(x^{'})$ 用当前的估计的值函数来代替真实的值函数，即：
$\theta = \theta + \alpha(r+\gamma V^{\pi}(x^{'})-\theta^Tx)$
其中x’是下一时刻的状态。
在时序差分学习中需要状态-动作值函数以便于获取策略，这里一种简单的做法是令 $\theta$ 作用于表示状态和动作的联合向量上，下面有两个例子：

给x增加一维用于存放动作编号如{1,2…}，然后与x进行合并为(x,a)
将动作进行编码，如01的稀疏编码，这个时候a就有很多维度了，再与x进行合并为(x,a)
把(x,a)与 $\theta$ 相乘求得的值作为状态-动作值函数的近似。

基于上述的方式，就可以得到了线性值函数近似的Sarsa算法：

也可以用其他方法来代替线性学习器，如引入核方法实现非线性值函数近似。

5. 模仿学习

在强化学习的经典任务设置中，机器所能获得的反馈信息仅有多步决策后的累积奖赏，但在现实任务中，往往能得到人类专家的决策过程范例，例如在种瓜任务上能得到农业专家的种植过程范例。从这样的范例中学习，称为"模仿学习"(Imitation learning)。

5.1 直接模仿学习

强化学习任务中多步决策的搜索空间巨大，基于累积奖赏来学习很多步之前的合适决策非常困难。而直接模仿人类专家的"状态-动作对可以显著缓解这一困难，我们称其为"直接模仿学习"。
所谓直接模仿学习，就是我们根据专家的决策轨迹数据，然后构造训练集，即把状态作为特征，动作作为标记，使用回归(连续)或者分类(离散)的学习算法即可获得策略模型。

5.2 逆强化学习

在很多任务中，设计奖赏函数往往相当困难，从人类专家提供的范例数据中反推出奖赏函数有助于解决该问题，这就是逆强化学习(inverse reinforcement learning)。
在逆强化学习中，我们知道状态空间X，动作空间A，并且与直接模仿学习类似，有一个决策轨迹数据集。逆强化学习的基本思想是:欲使机器做出与范例一致的行为，等价于在某个奖赏函数的环境中求解最优策略，该最优策略所产生的轨迹与范例数据一致。换言之，我们要寻找某种奖赏函数使得范例数据是最优的，然后即可使用这个奖赏函数来训练强化学习策略。
假设奖赏函数能表达为状态特征的线性函数 $R(x)=w^Tx$ ，于是策略 $\pi$ 的累积奖赏可写为：
$\rho^{\pi}=E[\sum_{t=0}^{+\infty}\gamma_tR(x_t)|\pi] \\ =E[\sum_{t=0}^{+\infty}\gamma_tw^Tx|\pi] \\ =w^TE[\sum_{t=0}^{+\infty}\gamma_tx|\pi]$
即为状态向量加权和的期望与系数w的内积。
采用蒙特卡罗方法通过采样来近似期望，而范例数据恰好可以看成是最优策略的一个采样。于是可以将每条范例轨迹上的状态加权求和再平均。

显然，我们难以获得所有策略，一个较好的办法是从随机策略开始，迭代地求解更好的奖赏函数，基于奖赏函数获得更好的策略，直至最终获得最符合范例轨迹数据集的奖赏函数和策略。这就是逆强化学习算法：