从零开始-Machine Learning学习笔记(10)-SVM支持向量机

  1995年，苏联的弗拉基米尔·瓦普尼克(Vladimir N. Vapnik)在Machine Learning上发表了最初的SVM文章。传统的统计模式识别方法只有在样本趋向无穷大时，其性能才有理论的保证。统计学习理论（STL）研究有限样本情况下的机器学习问题。SVM的理论基础就是统计学习理论。

  SVM以训练误差作为优化问题的约束条件，以置信范围值最小化作为优化目标，即SVM是一种基于结构风险最小化准则的学习方法，其推广能力明显优于一些传统的学习方法。

1.线性可分支持向量机

  给定线性可分训练数据集D，分类学习的最基本想法就是基于训练集D在样本空间中找到一个划分超平面。但是这样的划分超平面可能有很多，所以SVM的任务就是去找到这么一个划分超平面，即对训练样本局部扰动的“容忍性”最好，由此划分超平面所产生的分类结果是最具有鲁棒性的，对未见样本的泛化能力最强。

  在样本空间中，划分超平面可以通过如下的线性方程来描述：

$$w^Tx+b=0$$
  显然，划分超平面可以被法向量w和位移b确定，我们将其记为(w,b)。那么空间中任意一点到划分超平面的距离可以写为：
$$r = \frac{|w^Tx+b|}{||w||}$$
  上面这个式子中 $||w||$是表示w的范数，所谓范数就是一种计算方式，在欧式(欧几里得)空间 $R^n$中，范数定义为：
$$||w|| = \sqrt{w_1^2+w_2^2+...+w_n^2}$$
所以，有了这层知识，上面距离的表达式换算成三维空间中就是我们学过的最基础的点到平面的距离公式。

  假设超平面可以正确分类，即对于每个样本$(x_i,y_i)$有：

$$\begin{cases} w^Tx_i+b\geq +1, y_i = +1\\ w^Tx_i+b\leq -1, y_i = -1 \end{cases}$$
距离分离超平面最近的样本，他们能使上述的等号成立，因此被称作为“支持向量”(support vector)，而两个异类的支持向量到超平面距离之和我们称之为“间隔”(margin)。
$$\gamma = \frac{2}{||w||}$$

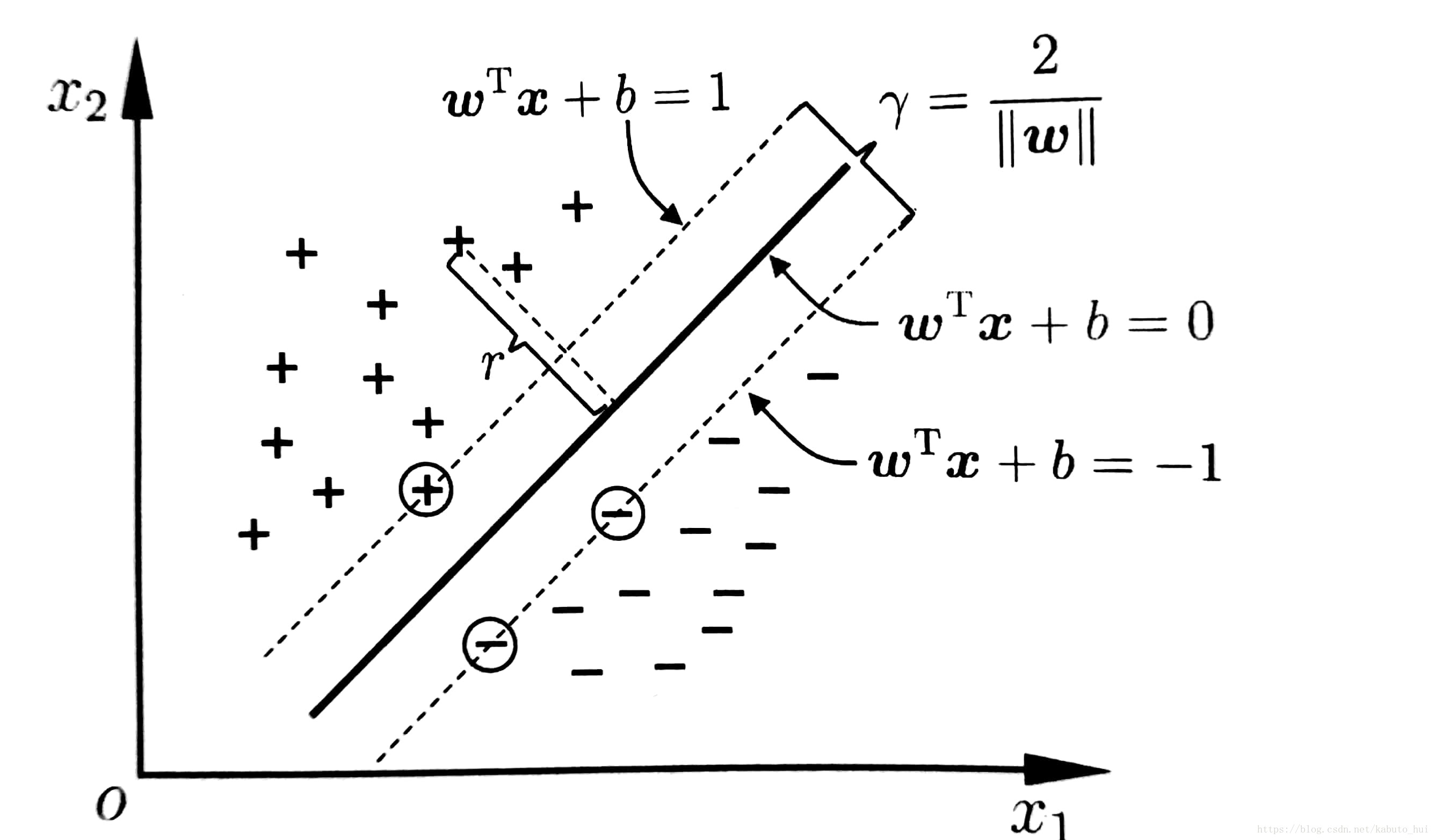
所以问题就可以转化为，找到满足上述约束条件的w与b，使得“间隔”最大。即：

$$\max_{w,b}{\frac{2}{||w||}} \\s.t.\ \ y_i(w^Txi+b) \ge1 , \ i=1,2,3...,m$$
于是可以转化为求其等价问题：
$$\min_{w,b}{\frac{1}{2}||w||^2} \\s.t.{ \ \ y_i(w^Txi+b) \ge1,i=1,2,3...,m}$$
我们使用拉格朗日乘子法，给每一个约束条件都添加一个拉格朗日乘子 $\alpha_i \geq 0$，所以其拉格朗日函数可以写为：
$$L(w,b,\alpha) = \frac{1}{2}||w||^2+\sum_{i=1}^{m}\alpha_i(1-y_i(w^Tx+b))$$
分别让L对w，b求偏导数并使其等于0可以得到：
$$w = \sum_{i=1}^{m}\alpha_iy_ix_i \\ 0 = \sum_{i=1}^{m}\alpha_iy_i$$
把上述两式带回拉格朗日函数中可以得到最终的一个对偶问题：
$$\begin{array}{l} \mathop {\min }\limits_\alpha \;\;\;\frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right)} } - \sum\limits_{i = 1}^N {{\alpha _i}} \\ s.t.\;\;\sum\limits_{i = 1}^N {{\alpha _i}{y_i} = 0} \\ \;\;\;\;\;{\alpha _i} \ge 0,\;\;\;\;i = 1,2, \ldots ,N \end{array}$$
最后求得最优解 $\alpha^*$。

再根据$\alpha^*$可以求出w与b：

$$\begin{array}{l} w^* = \sum\limits_{i = 1}^m {\alpha _i^*{y_i}{x_i}} \\ b^* =y_j - w^Tx= {y_j} - \sum\limits_{i = 1}^m {\alpha _i^*{y_i}\left( {{x_i} \cdot {x_j}} \right)} \end{array}$$
特别说明：

在计算$\alpha$时，我们可以写出其KKT条件如下：

$$\begin{cases} \alpha_i \geq 0 \\ y_if(x_i)-1 \geq 0\\ \alpha_i(y_if(x_i)-1) = 0 \end{cases}$$
当 $(x_i,y_i)$ 不是支持向量的时候，一定有 $y_if(x_i)-1 \geq 0\\$成立，那么根据第三个条件可以得出 $\alpha_i = 0$。所以这也解释了 支持向量机的最终模型仅与支持向量有关。

2.线性不可分支持向量机

  若o若数据线性不可分，则增加松弛因子$ξ_i≥0$，使函数间隔加上松弛变量大于等于1。这样，约束条件变成:

$${y_i}\left( {w \cdot {x_i} + b} \right) \ge 1 - {\xi _i}$$
目标函数则变为：
$$\mathop {\min }\limits_{w,b} \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^m {{\xi _i}}$$
所以原来的优化问题就变为：
$$\begin{array}{l} \mathop {\min }\limits_{w,b,\xi } \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^m {{\xi _i}} \\ s.t.\;\;\;{y_i}\left( {w \cdot {x_i} + b} \right) \ge 1 - {\xi _i},\;\;\;i = 1,2, \cdots m\\ \;\;\;\;\;\;{\xi _i} \ge 0,\;\;\;i = 1,2, \cdots m \end{array}$$
此时，拉格朗日函数为：
$$L\left( {w,b,\xi ,\alpha ,\mu } \right) \equiv \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^m {{\xi _i}} - \sum\limits_{i = 1}^m {{\alpha _i}\left( {{y_i}\left( {w \cdot {x_i} + b} \right) - 1 + {\xi _i}} \right)} - \sum\limits_{i = 1}^m {{\mu _i}{\xi _i}}$$
对w,b,ξ求偏导：
$$\frac{\partial L}{\partial w} = 0 \Rightarrow w=\sum_{i=1}^{m}\alpha_iy_ix_i \\ \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=0}^{m}\alpha_iy_i = 0 \\ C-\alpha_i - \mu_i = 0$$
带入L中得到：
$$\mathop {\min }\limits_{w,b,\xi } L\left( {w,b,\xi ,\alpha ,\mu } \right) = - \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right)} } + \sum\limits_{i = 1}^N {{\alpha _i}}$$
对上式关于 $\alpha$求极大，并求其对偶问题：
$$\begin{array}{l} \mathop {\min }\limits_\alpha \;\;\;\frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right)} } - \sum\limits_{i = 1}^m {{\alpha _i}} \\ s.t.\;\;\sum\limits_{i = 1}^m {{\alpha _i}{y_i} = 0} \\ \;\;\;\;\;0 \le {\alpha _i} \le C,\;\;\;\;i = 1,2, \ldots ,m \end{array}$$
求得最优解α*，计算w与b：
$$\begin{array}{l} w* = \sum\limits_{i = 1}^m {\alpha _i^*{y_i}{x_i}} \\ b* = {y_j} - \sum\limits_{i = 1}^m {\alpha _i^*{y_i}\left( {{x_i} \cdot {x_j}} \right)} \end{array}$$
注意：计算b*时，需要满足0<αj