参考视频 https://www.bilibili.com/video/av4356232/
参考博客 https://blog.csdn.net/codesamer/article/details/81191487
目录
1.预测值 与 状态预测公式
假设有一个小车在行驶,它的状态是,包括它的 位置p 和 速度v,加速度u

可知其上一时刻的状态为
发现其输出变量是输入变量的线性组合

转化成矩阵的形式为
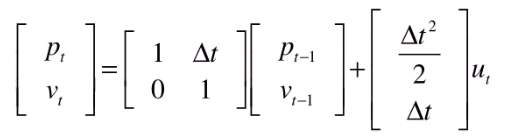
令 F 为状态转移矩阵(从上一时刻的状态推测这个时刻的状态),B 为控制矩阵(控制量u如何作用当前状态)
得到状态预测公式
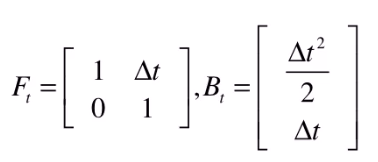

1.1预测状态的协方差P
使用协方差矩阵来表示 预测的值 的不确定性

假设 x 、y 两个维度的随机变量相互独立,其协方差为0
假设 x 、y 两个维度的随机变量具有相关性,x 随着 y 增大 协方差>0 。x 随着 y 减小 协方差<0
协方差矩阵表示为 cov(x,x) 对角线表示两个维度的 随机变量的 方差。斜对角线的值相等,表示协方差
根据: ![]()
不确定性 在各个时刻的传递关系(预测状态的协方差)
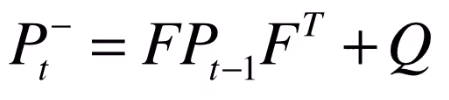
加一个 协方差Q 表示预测模型本身带来的噪声
1.2观测值 与 观测噪声协方差R
一个观测量 Z 可以通过车辆当前的状态 x · 观测矩阵H 和一个误差组成
定义观测噪声的协方差矩阵为 R

2.1状态更新
有第一步等到带 - 号的预测值,通过观测量修正 x 的值,就可以得到一个最佳估计值
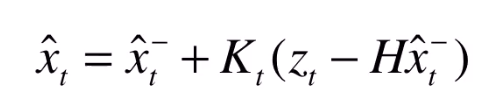
括号里面代表实际的观测值 和 预期的观测值 的残差。
K 是卡尔曼系数
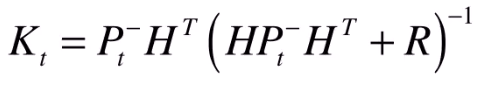
作用1:
权衡预测状态协方差 P 和 观测噪声协方差 R 的大小。来决定相信预测多一些(K小) or 相信观察多一些(K大)
作用2:
把残差的表现形式 从观察域 转化到 状态域
2.2预测值的噪声分布(协方差)P 的更新
更新 最佳预测值的噪声分布 未了 下一轮迭代
在不确定性变化(噪声)中寻找一个平衡
![]()
整合
带 - 的值是预测的值,但是缺少观测值的修正。所以加入观测值后,对每一时刻的状态进行预测。

公式1: X(k|k-1) = AX(k-1 | k-1) + BU(k) + W(k)
公式2: P(k|k-1) = AP(k-1|k-1)A' + Q(k)
公式3: X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)
公式4: Kg(k) = P(k|k-1)H'/{HP(k|k-1)H' + R}
公式5 : P(k|k) = (1- Kg(k) H) P(k|k-1)
实现
# -*- coding: utf-8 -*-
"""
Created on Tue Jan 1 15:54:48 2019
@author: aligo
"""
import numpy as np
import matplotlib.pyplot as plt
# 观测值,1-100 每秒一部,就是速度为 1 的匀速行驶
z = [i for i in range(100)]
z_watch = np.mat(z)
# 创建一个方差为1的高斯噪声,精确到小数点后两位
noise = np.round(np.random.normal(0, 1, 100), 2)
noise_mat = np.mat(noise)
# 将z的观测值和噪声相加
z_mat = z_watch + noise_mat
#print(z_watch)
# 定义x的初始状态
x_mat = np.mat([[0,], [0,]])
# 定义初始状态协方差矩阵
p_mat = np.mat([[1, 0], [0, 1]])
# 定义状态转移矩阵,因为每秒钟采一次样,所以delta_t = 1
f_mat = np.mat([[1, 1], [0, 1]])
# 定义状态转移协方差矩阵,这里我们把协方差设置的很小,因为觉得状态转移矩阵准确度高
q_mat = np.mat([[0.0001, 0], [0, 0.0001]])
# 定义观测矩阵
h_mat = np.mat([1, 0])
# 定义观测噪声协方差
r_mat = np.mat([1])
for i in range(100):
x_predict = f_mat * x_mat
p_predict = f_mat * p_mat * f_mat.T + q_mat
kalman = p_predict * h_mat.T / (h_mat * p_predict * h_mat.T + r_mat)
x_mat = x_predict + kalman *(z_mat[0, i] - h_mat * x_predict)
p_mat = (np.eye(2) - kalman * h_mat) * p_predict
plt.xlabel("p")
plt.ylabel("v")
plt.plot(x_mat[0, 0], x_mat[1, 0], 'ro', markersize = 1)
plt.show()

横坐标表示离初始位置的距离 p,纵坐标表示在该位置的速度 v。
初始为0,在经过一段很短的时间后,速度预测值 与 实际值1 就很接近了