置换群&Polya计数简易版学习笔记

前言

这个定理其实我学了蛮久的，就是一直一直没有掌握，原因是太抽象，而且证明也没怎么理解，今天看了Candy？大佬的博客，结合自己少得可怜的抽象代数知识，总算是搞懂了一点点，赶紧来发一波blog

问题引入

抽象的东西自然要把它具象化。
给定一个正方形的四格棋盘，想要给它黑白染色。
显然共有以下16种方案。
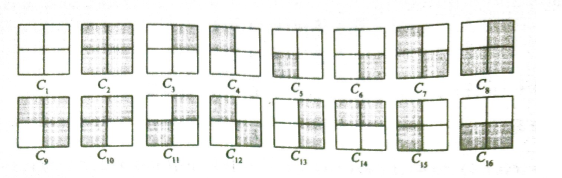
在这里插入图片描述
但是如果我认为，如果把正方形可以旋转 $90^\circ,180^\circ, 270^\circ$ ，求有多少种本质不同的正方形呢？
显然只有6种

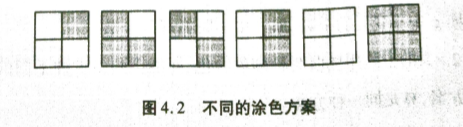
而置换群就是用来解决这一类问题的。

前置知识

概念1：置换

设 $N_n={1,2\cdots n}$ ，则从 $N_n$ 到 $N_n$ 上的一个双射 $f$ 称为一个置换，通常记为：
$f =\bigl( \begin{matrix} 1 & 2 \cdots & n \\ f(1) & f(2) \cdots & f(n) \end{matrix} \bigr)$
上述问题中的旋转就可认为是一种置换。

概念2：置换乘积

假设我们有置换 $f,g$ 那么
$(f\cdot g)(k)=f(g(k))$
通常不满足交换律，但满足结合律。

概念3：置换群

设集合 $N_n$ 的所有置换的集合为 $Sn$
$Sn$ 的非空子集 $G$ 满足：

合成运算的封闭性 $∀f,g∈G, f⋅g∈G$
单位元 $ι∈G$
逆元的封闭性 $∀f∈G, f^{−1}∈G$

那么 $G$ 就是一个置换群。
阶：置换群中元素个数
显然，上述问题的旋转组成了一个置换群。

概念4：置换群的消去律

$f⋅g=f⋅h→f^{-1}\cdot f⋅g=f^{-1}\cdot f⋅h→g=h$

概念5：着色

就是给 $N_n$ 中的每一个元素分配一个颜色。
设 $c$ 是 $N_n$ 的一种着色，用 $c(i)$ 表示 $i$ 的颜色。
上述问题的黑白染色就是一种着色。

概念6：置换对着色的作用

$f$ 将 $k$ 变为 $f(k)$ ，所以 $f∗c$ 将 $k$ 的颜色变到 $f(k)$
$(f∗c)(l)=c(f^{−1}(l)) l=1,2,...,n$
理解为旋转+染色即可。

概念7：着色集

$C$ 满足：
$∀f∈G,c∈C, f∗c∈C$

概念8：等价类

$∃f∈G, f∗c_1=c_2$ 则 $c_1\Leftrightarrow c_2$
就是说，存在旋转某个角度使得某种染色后的两个正方形相同，那么这两个正方形就是本质相同的，他们就在同一个等价类中。
而不同的等价类会把 $C$ 分成不同的几个部分。
而我们要求的，就是到底会把 $C$ 分成多少个等价类。

Burnside定理

终于开始了最重要的部分了。

概念1：稳定核

使着色 $c$ 不变的置换集合，称为 $c$ 的稳定核。也就是
$G(c)=f:f\in G, f*c=c$
也就是说，对于某种染色方案，置换完以后的状态和原来相同。

概念2：不动点

类似地，置换 $f$ 作用下不变的着色集合，称为 $f$ 的不动点。也就是
$C(f)=c:c\in C, f*c=c$

引理：轨道-稳定核定理

与 $c$ 等价的着色数
$orbit(c)=|f∗c: f∈G|=\frac{|G|}{|G(c)}$
等于 $G$ 中置换个数除以 $c$ 的稳定核中置换的个数
证明：
考虑有多少个 $g$ ,使得 $g∗c=f∗c$ ，也就是 $c$ 着色下的等价置换。
由于置换群 $G$ 的封闭性，咱们把 $g$ 拆成 $g=f\cdot h$
由之前的消去律可以得到
$(f\cdot h)*c=f*c\to h*c=c$
而 $G(c)=h:h\in G,h*c=c$
也就是说，这样的 $h$ 一共有 $|G(c)|$ 个（包括 $f$ 本身）。
也就是说，对于每个 $f$ 有 $|G(c)|$ 个置换与他的效果相同
那么与 $c$ 等价的着色数就是 $\frac{|G|}{|G(c)|}$ 啦
是不是很神奇？

定理：Burnside定理

主角登场！
着色集 $C$ 中非等价着色数
$N(G,C)=\frac{1}{|G|}∑_{f∈G}|C(f)|$
等于所有 $|C(f)|$ 的平均值
证明采用算二次方法。
我们用两种方法计数 $f∗c=c$ 的 $(f,c)$ 的个数
$\sum_{f\in G}|C(f)|=\sum_{c\in C}G(c)=|G|\sum_{c\in G}\frac{1}{orbit(c)}$
刚才的引理排上了大用场。
这个时候考虑 $\sum_{c\in G}\frac{1}{orbit(c)}$ 的组合意义。
每一个等价类的大小是 $orbit(c)$
那么一个等价类在上面的式子中的总贡献就是
$orbit(c)\cdot\frac{1}{orbit(c)}=1$
这就意味着！
$\sum_{c\in G}\frac{1}{orbit(c)}=N(G,C)$
证完了！

小试牛刀：Burnside定理的应用

考虑上面那道题
列出所有的置换，把不动点数出来。
在这里插入图片描述
是不是特别的。。。。
不好用呢？
复杂度甚至比暴力更高。
所以很多人称 $Burnside$ 为引理。
因为真正的神器在后面。

Polya定理

循环

它的严格定义是这样的。
设 $f$ 是 $N_n$ 上的一个置换， $a_1,a_2\cdots a_n$ 是 $1,2\cdots n$ 上的一个排列，如果 $f(a_1)=a_2,f(a_2)=a_3\cdots f(a_{k-1})=a_k,f(a_k)=a_1$ ，而且当 $k<n$ 时有 $f(a_{k+1})=a_{k+1}\cdots f(a_n)=a_n$ ，那么称 $f$ 是一个 $k$ 阶循环。
简单地来说，就是沿着 $f$ 跑出了一个环，这个环的大小是 $k$ ，除了这个环之外都是不动点的置换k阶循环。
显然，一个置换可以拆成若干个循环。
从图论的角度来看这个问题会比较清晰。
将置换看成有向图
$D_f=(N_n,E_f), E_f=(i,f(i)): i∈N_n$
$n$ 个点 $n$ 个弧
可以划分成若干个有向环，每个有向环是一个循环置换
阶为1的循环就是恒等置换
如果把置换看成连边的话，由于是双射，所以每个点入度出度都恰好为1，所以置换构成的图肯定是几个简单环构成的。
严格证明要数归，在此咕咕咕。

Polya定理

设循环的个数 $\#(f)$ ，用 $k$ 种颜色着色，
那么 $|C(f)|=k^{\#(f)}$
证明：显然 $f$ 作用下不变的着色每一个循环中着色必须相同。
$N(G,C)=\frac{1}{|G|}∑_{f∈G}k^{\#(f)}$
在这里插入图片描述

这样计算是不是快多了！

Polya定理的一点点小拓展

有一个局限是 $Ploya$ 定理要求染色数目不限制。
如果说颜色的种类数给定怎么破？
考虑用 $Burnside$ 引理证明 $Polya$ 定理的时候。
把每个置换拆成了若干个循环，而每个循环的着色必须相同。
那么颜色有限制的话，对于每个置换而言，相当于是要用若干个颜色填充几个循环节。
把循环节看成物品，颜色看成背包做多维背包Dp即可。

后记

写完之后就一个字：爽！
很实用的一个定理，理解其实也不需要太高大上的数学功底。
好玩好玩。。。（皮得一匹耶）