数值分析用matlab求解三次样条插值多项式

时间真快，2018年只剩下2天，2019年即将来临！
今晚整理笔记本中的资料，看了下之前给朋友解答的一个《数值分析》实验题目，还是有点意思。不管怎样，分享给需要的朋友，希望有所帮助！

给定函数，及节点如下：

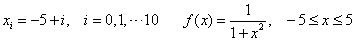
求其三次样条插值多项式（可取I型或II型边界条件），并画图及与的图形进行比较分析。

实验过程及主函数代码

%%
%程序功能：三次样条插值多项式
%运行方式：运行主程序main3.m
%程序输出：三次样条插值函数图像、原函数图像
%%
clear all; close all; clc;
%% 原函数初始化，以便与三次样条插值多项式进行对比
syms x
f = 1 ./ (1 + x.^2);
f1d = diff(f, x, 1);    %diff(f, x, n)表示f对x求n次导数
f2d = diff(f, x, 2);
%% 给出边界条件，选取I型边界条件
x = -5;
S1d_left = subs(f1d);
x = 5;
S1d_right = subs(f1d);
%% 给出插值节点及其相应函数值
xSample = linspace(-5,5,11);   %在区间[-5,5]内等距离选取11个节点
x = xSample;
fSample = subs(f);
n = length(x);                 %读取采样节点的个数
%% 求取系数矩阵A
lamda = 1/2 * ones(1,n-1);
lamda(1) = 1;               %令λ0 = 1
miu = 1/2 * ones(1,n-1);    %H(j+1)/( H(j-1) + H(j) )
miu(10) = 1;                %令μn = 1, n = 10
delta = zeros(1,n);
A = zeros(n,n);
Lam = 1;                    %令λ0 = 1
Miu = 1;                    %令μn = 1, n = 10
for i = 1 : n
    for j = 1 : n
        if j-i == 1
            A(i,j) = lamda(Lam);
            Lam = Lam + 1;
        end
        if i-j == 1
            A(i,j) = miu(Miu);
            Miu = Miu + 1;
        end
    end
end
%% 根据公式推导求取delta向量
for i = 1 : n
    if i == 1
        delta(1) = 6 * (( fSample(2) - fSample(1) ) - S1d_left);
    elseif i == n
        delta(n) = 6 * (S1d_right - ( fSample(n) - fSample(n-1) ));
    else
        delta(i) = 6 * ( fSample(i+1) + fSample(i-1) - 2*fSample(i)) / 2;
    end
    A(i,i) = 2;
end
%% 求解基本方程矩阵Am=d，求取m关系向量
m = inv(A) * delta';               %求解Am=d方法：m =inv(A)*b' = A\d' = inv(A'*A)*A'*b'
syms S1 S2 S3 S4 S5 S6 S7 S8 S9 S10
S=[S1 S2 S3 S4 S5 S6 S7 S8 S9 S10];%插值函数分为10段
syms x
for i = 1 : n-1
    S(i) = m(i) / 6*(-5+i-x)^3 + m(i+1) / 6*(x+6-i)^3 ...
        + (fSample(i) - m(i)/6) * (-5+i-x) + (fSample(i+1) - m(i+1)/6) * (x+6-i);
end
%% 显示其三次样条插值多项式的分段表达式
disp('Three cubic spline interpolation polynomials : S(x) =')
disp(S)
%% 绘制原函数和三次样条插值多项式的曲线
figure
x = -5 : 0.01 : 5;
plot(x, subs(f), '-k');
hold on;
plot(xSample, fSample,'ob');
hold off;
hold on;
for i = 1 : n-1
    x = -6+i : 0.01 : -5+i;
    plot(x, subs(S(i)), '-r');
end
hold off;
legend('f = 1/(1+x^2)曲线','采样点','3 Spline插值曲线')

实验结果及分析

由图可知，三次样条插值函数不仅光滑度很高，而且要求求解时还不需要增加内节点处的导数值，因此比较实用。三次样条插值解决了Newton插值多项式在高次插值所出现的龙格现象。

致谢
若对大家有用，感谢点赞或评论；若有不足或补充之处，也感谢大家评论进行指正，后期我将对本文进行补充完善。相信这是互相进步的开始！

数值分析用matlab求解三次样条插值多项式

数值分析用matlab求解三次样条插值多项式

实验过程及主函数代码

实验结果及分析

猜你喜欢