六轴机器人轨迹规划之三次多项式轨迹插值

1.轨迹规划的定义
轨迹规划(trajectory planning)是运动规划(motion planning)研究的主要内容。运动规划指的是运动插补，在起始点和终止点之间插入中间点序列，实现沿着轨迹的平稳运动。运动控制包含路径规划(path planning)和轨迹规划，路径规划是规划位置，在起终点之间经过的路径点，轨迹规划是规划时间，将路径点与时间相对应。
对于我们的六轴机器人而言轨迹规划可以分为：关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划是把机器人的关节变量变换成跟时间的函数，然后对角速度和角加速度进行约束。笛卡尔空间轨迹规划是把机器人末端在笛卡尔空间的位移、速度和加速度变换成跟时间的函数关系。
2.数学基础
三次多项式插值（适用于起点和终点速度为零的情况，约束关节在起点和终点的角度值，规定轨迹两端点位置角速度为定值）。
设关节角满足下式

\begin{array}{rcl} {\begin{cases} θ (t) = a_{0} + a_{1} t + a_{2} t^{2} + a_{3} t^{3} \\ \dot{θ} (t) = a_{1} + 2 a_{2} t + 3 a_{3} t^{2} \\ \ddot{θ} (t) = 2 a_{2} + 6 a_{3} t \end{cases} \end{array}

$\begin{eqnarray*} \left\{ \begin{array}{l} \theta(t)=a_0+a_1t+a_2t^2+a_3t^3\\ \dot{\theta}(t)=a_1+2a_2t+3a_3t^2\\ \ddot{\theta}(t)=2a_2+6a_3t \end{array}\right. \end{eqnarray*}$
将相邻两个点看作一小段轨迹的起点和终点分别用

θ_{0}

$\theta_0$ 和

θ_{f}

$\theta_f$ 表示，约束起始速度为

v_{0}

$v_0$ ，终止速度为

v_{f}

$v_f$

\begin{array}{rcl} {\begin{cases} θ (t_{0}) = θ_{0} \\ θ (t_{f}) = θ_{f} \\ \dot{θ} (t_{0}) = v_{0} \\ \dot{θ} (t_{f}) = v_{f} \end{cases} \end{array}

$\begin{eqnarray*} \left\{ \begin{array}{l} \theta(t_0)=\theta_0\\ \theta(t_f)=\theta_f\\ \dot{\theta}(t_0)=v_0\\ \dot{\theta}(t_f)=v_f\\ \end{array}\right. \end{eqnarray*}$
将约束条件代入函数，可以求得系数（为简便计算，设

t_{0} = 0

$t_0=0$ ）

\begin{array}{rcl} {\begin{cases} a_{0} = θ_{0} \\ a_{1} = v_{0} \\ a_{2} = \frac{3}{t_{f}^{2}} (θ_{f} - θ_{0}) - \frac{1}{t_{f}} (2 v_{0} + v_{f}) \\ a_{3} = \frac{2}{t_{f}^{3}} (θ_{0} - θ_{f}) + \frac{1}{t_{f}^{2}} (v_{0} + v_{f}) \end{cases} \end{array}

$\begin{eqnarray*} \left\{ \begin{array}{l} a_0=\theta_0\\ a_1=v_0\\ a_2=\frac{3}{t_f^2}(\theta_f-\theta_0)-\frac{1}{t_f}(2v_0+v_f)\\ a_3=\frac{2}{t_f^3}(\theta_0-\theta_f)+\frac{1}{t_f^2}(v_0+v_f)\\ \end{array}\right. \end{eqnarray*}$
三次多项式规划轨迹如下

\begin{array}{rcl} {\begin{cases} θ (t) = θ_{0} + v_{0} t + [\frac{3}{t_{f}^{2}} (θ_{f} - θ_{0}) - \frac{1}{t_{f}} (2 v_{0} + v_{f})] t^{2} + [\frac{2}{t_{f}^{3}} (θ_{0} - θ_{f}) + \frac{1}{t_{f}^{2}} (v_{0} + v_{f})] t^{3} \\ \dot{θ} (t) = v_{0} + 2 [\frac{3}{t_{f}^{2}} (θ_{f} - θ_{0}) - \frac{1}{t_{f}} (2 v_{0} + v_{f})] t + 3 [\frac{2}{t_{f}^{3}} (θ_{0} - θ_{f}) + \frac{1}{t_{f}^{2}} (v_{0} + v_{f})] t^{2} \\ \ddot{θ} (t) = 2 [\frac{3}{t_{f}^{2}} (θ_{f} - θ_{0}) - \frac{1}{t_{f}} (2 v_{0} + v_{f})] + 6 [\frac{2}{t_{f}^{3}} (θ_{0} - θ_{f}) + \frac{1}{t_{f}^{2}} (v_{0} + v_{f})] t \end{cases} \end{array}

$\begin{eqnarray*} \left\{ \begin{array}{l} \theta(t)=\theta_0+v_0t+[\frac{3}{t_f^2}(\theta_f-\theta_0)-\frac{1}{t_f}(2v_0+v_f)]t^2+[\frac{2}{t_f^3}(\theta_0-\theta_f)+\frac{1}{t_f^2}(v_0+v_f)]t^3\\ \dot{\theta}(t)=v_0+2[\frac{3}{t_f^2}(\theta_f-\theta_0)-\frac{1}{t_f}(2v_0+v_f)]t+3[\frac{2}{t_f^3}(\theta_0-\theta_f)+\frac{1}{t_f^2}(v_0+v_f)]t^2\\ \ddot{\theta}(t)=2[\frac{3}{t_f^2}(\theta_f-\theta_0)-\frac{1}{t_f}(2v_0+v_f)]+6[\frac{2}{t_f^3}(\theta_0-\theta_f)+\frac{1}{t_f^2}(v_0+v_f)]t \end{array}\right. \end{eqnarray*}$
当速度为零时适用于一段轨迹的起终点，不为零时适用于一段轨迹的经过点。
3.matlab代码实现

序号	位置	速度	时间
1	0	0	0
2	100	0	3

clear;
clc;
q0=0;
q1=100; %指定起止位置
t0=0;
t1=3;%指定起止时间
v0=0;
v1=0;%指定起止速度
a0=q0;
a1=v0;
a2=(3/(t1)^2)*(q1-q0)-(1/t1)*(2*v0+v1);
a3=(2/(t1)^3)*(q0-q1)+(1/t1^2)*(v0+v1);%计算三次多项式系数
t=t0:0.01:t1;
q=a0+a1*t+a2*t.^2+a3*t.^3;%三次多项式插值的位置
v=a1+2*a2*t+3*a3*t.^2;%三次多项式插值的速度
a=2*a2+6*a3*t;%三次多项式插值的加速度
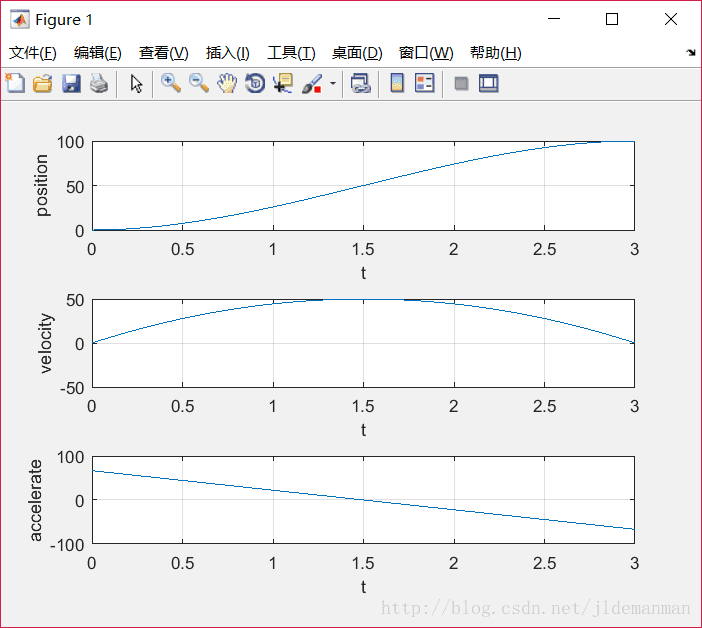
subplot(3,1,1),plot(t,q),xlabel('t'),ylabel('position');grid on;
subplot(3,1,2),plot(t,v),xlabel('t'),ylabel('velocity');grid on;
subplot(3,1,3),plot(t,a),xlabel('t'),ylabel('accelerate');grid on;

下图为插值结果
这里写图片描述
4.含经过点的插值

序号	位置	速度	时间
1	0	0	0
2	50	10	3
3	150	20	6
4	100	-15	12
5	0	0	14

clear;
clc;
q_array=[0,50,150,100,0];%指定起止位置
t_array=[0,2,4,8,10];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[0];%初始状态
for i=1:1:length(q_array)-1;%每一段规划的时间
     a0=q_array(i);
     a1=v_array(i);
     a2=(3/(t_array(i+1)-t_array(i))^2)*(q_array(i+1)-q_array(i))-(1/(t_array(i+1)-t_array(i)))*(2*v_array(i)+v_array(i+1));
     a3=(2/(t_array(i+1)-t_array(i))^3)*(q_array(i)-q_array(i+1))+(1/(t_array(i+1)-t_array(i))^2)*(v_array(i)+v_array(i+1));%计算三次多项式系数 
     ti=t_array(i)+0.001:0.001:t_array(i+1);
     qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3;
     vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2;
     ai=2*a2+6*a3*(ti-t_array(i));
     t=[t,ti];q=[q,qi];v=[v,vi];a=[a,ai];
end
subplot(3,1,1),plot(t,q,'r'),xlabel('t'),ylabel('position');grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t'),ylabel('velocity');grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t'),ylabel('accelerate');grid on;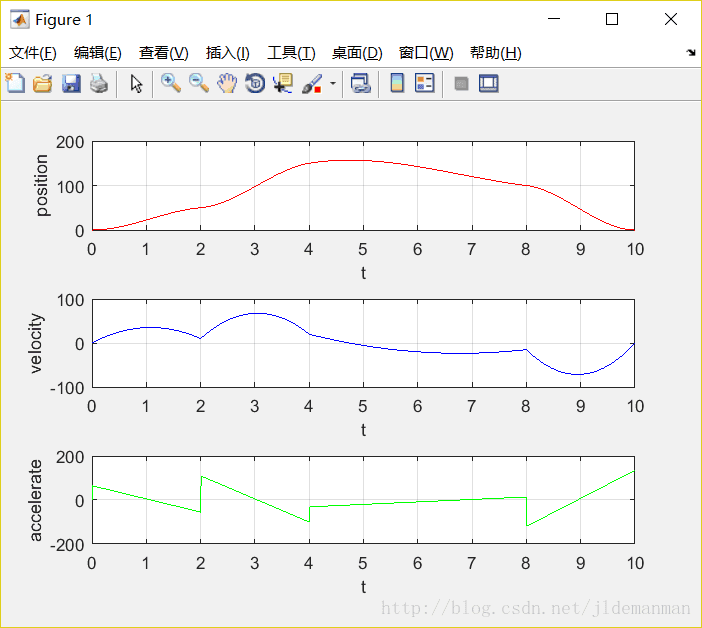

这里写图片描述
PS:这种三次多项式插值，只要给定离散点位置、速度和时间，就能插补出一段连续平滑的曲线。但是角加速度并不连续，下次为大家介绍高阶多项式插值则可以解决这个问题。

六轴机器人轨迹规划之三次多项式轨迹插值

猜你喜欢