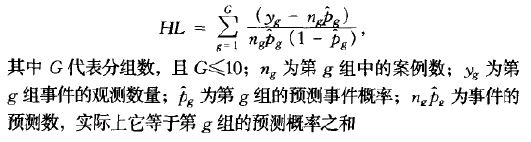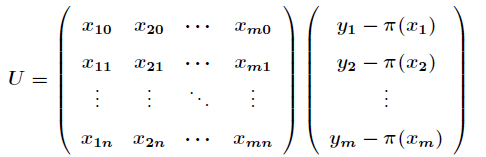第3章-从线性概率模型到广义线性模型(1)

一，模型

1，二值因变量模型

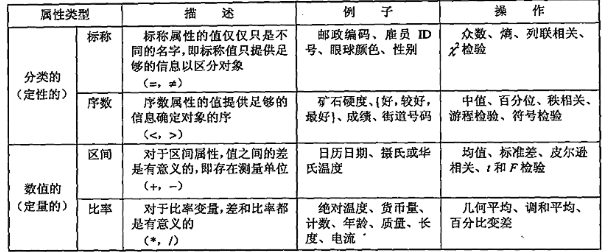
在统计学中，数据的属性有两大类：数值型的和分类型的。分类的属性又分为标称的以及序数的，数值的属性会分为区间的和比率的。参考下图所示：

通常在模型中，自变量 $x$会有分类型的和数值型的属性同时出现的情况。其中分类的属性通常是二值的，如果不是二值的，会拆分成n-1个二值属性进行建模(n为分类属性的类别个数)，统计学上又称这种二值变量为虚拟变量或哑变量。

同理，因变量也会出现 $y$不是数值型的情况，通常研究分类模型都是从假定 $y$为二值变量时开始。不过当因变量为多分类时，也可以拆分成n-1个二分类模型进行集成，或者直接构建多分类模型(假定 $y$是服从多项式分布)。因变量还可能为有序分类等其他情况。鉴于这些情况较为复杂，打算在后续文章逐步进行阐述。本文仅讨论当因变量y为二值变量时的情况。

我们先从线性概率模型(Linear Probability Model，LPM)谈起。

2，线性概率模型
我们知道简单的多元线性模型可以写成下面的形式：

$y$= $\beta$₀+ $\beta$₁ $x$₁+ $\beta$₂ $x$₂+…+ $\beta$_n $x$_n+ $u$

那么当 $y$为二值时(即只取0或1时)，我们用样本回归函数估计出的 $y$值又有什么含义呢？

在给定x下，y的期望值为如下方程：

$E(y|x)$= $\beta$₀+$\beta$₁ $x$₁+ $\beta$₂$x$₂+…+$\beta$_n $x$_n

(注：我们总是假定残差u与x是独立的且具有零均值，同方差的性质。所以E(u|x)=E(u)=0)

根据上面的公式可知，当y是一个取值0和1的二值变量时，y的期望值等于"y=1"的条件概率总是成立的。
即， $E(y|x)$=1P(y=1|x)+0P(y=0|x)=P(y=1|x)，于是我们得到了一个重要的方程：

$P(y=1|x)$= $\beta$₀+ $\beta$₁ $x$₁+ $\beta$₂ $x$₂+…+ $\beta$_n $x$_n

该方程说明了概率p(x)=P(y=1|x)是 $x$_i的一个线性函数。而P(y=1|x)也被称为响应概率(response probability)。由于概率和必须等于1，所以P(y=0|x)=1-P(y=1|x)也是 $x$_i的一个线性函数。

因为这个响应概率是参数 $\beta$_i的线性函数，所以这种二值因变量的多元线性模型又称为线性概率模型。

3，线性概率模型的局限

(1)由线性概率模型的公式可知，当 $x$_i的取值变化时，无法保证概率的取值范围在0~1之内。

(2)LPM违背了一个高斯-马尔可夫定理(Gauss–Markov theory)假定。当y是一个二值变量时，其以 $x$为条件的方差为
Var(y|x)=p(x)[1-p(x)]
其中，p(x)= $\beta$₀+ $\beta$₁ $x$₁+ $\beta$₂ $x$₂+…+ $\beta$_n $x$_n，这意味着，除非概率与任一 $x$均不相关，否则一定存在异方差问题，即方差的非齐性。

4，线性概率模型的改进

虽然LPM很简单实用，但是因为有上述2点的不足，拟合出来的概率也可能会超过0~1的范围。为此，我们需要使用更为复杂的二值响应模型来克服这些缺点。

在一个响应模型中，我们关注的是响应概率
P(y=1|x)=P(y=1| $x$₁, $x$₂,…, $x$_n)

在LPM中，我们假定了响应概率是一系列参数 $\beta$_i的线性方程。为了避免LPM的局限，我们可以扩展方程的类型，考虑如下方程：

$P(y=1|x)$=G( $\beta$₀+ $\beta$₁ $x$₁+ $\beta$₂ $x$₂+…+ $\beta$_n $x$_n)=G( $\beta$₀+x $\beta$)=G(x $\beta$)
（令原x={ $x$₁, … , $x$_n},扩展为x={ $x$₀=1， $x$₁, … , $x$_n}，模型表达即简化为G(x $\beta$)）

其中，G()是一个取值范围严格介于0_{1之间的单调函数，这就确保了响应概率也严格的介于0}1之间。G()的形式与选择有很多种，当G()为线性的，就是上面提到的LPM，除此之外，比较广泛使用的非线性的形式有logit及probit。

logit：G(x)= $\frac{exp(x)}{1+exp(x)}$
当G()是一个标准的Logistic随机变量的累计分布函数。

probit：G(x)= $\int$ $\frac{1}{\sqrt{2\pi}}$exp(- $\frac{x^2}{2}$)dx
当G()是一个标准的正态随机变量的累计分布函数。

备注：
(1) G()函数除了取上述形式，还有其他指数型，以及log型，双曲正弦型等其他类型。

(2) 根据AngrewNg的机器学习课程中的讲解，得知当P(x|y=1)服从指数分布族，则P(y=1|x)的后验分布就服从Logistics分布。

5，改进的模型的推导

logit和probit模型都可以从一个满足经典线性模型假定的潜变量模型(latent variable model)推导出来。

令 $y$为一个由下式决定的观测不到的潜变量。
$y$=x $\beta$+u
y=1，when $y$>0
y=0，when $y$<=0

假定：残差u独立于x，并且服从标准的整体分布或标准的Logistics分布。

P(y=1|x)=P( $y$*>0|x)=P(xβ+u>0|x)=P(u>-xβ|x)=1-G(-xβ) =G(xβ)
(因为假定模型的残差u与x无关，且不论是Logistics还是probit，残差的分布都是对称的)

所以，改进的二值响应概率模型，实际上取决于对残差u的假设，当u服从正态分布，则模型为probit，当u服从logistic分布则模型为logistic。

probit模型中，残差项u的方差为1；Logistics模型中，残差项u的方差为 $\pi$²/3；

6，模型的参数估计-极大似然估计

极大似然估计与OLS估计的统计性质几乎相同。具有一致性、渐进有效性、渐进正态性。与OLS估计不同之处是，只有在样本较大时，似然估计的性质才能够保持。极大似然估计的样本量在100以上时，风险会小很多(Aldrich and Nelson,1984).

接下来我们看看，一般情况下是如何推导似然估计的：

已知，P(y=1|x)=G(xβ) ，P(y=0|x)=1-G(xβ)
假设自变量x的个数为n个，加上常数项x₀=1的扩展，x向量的长度为n+1，同时假定样本量为m个。

我们定义y_i在给定x_i下的概率密度：
f(y_i|x_i,β)=G(x_iβ)^y_i[1-G(x_iβ)]^1-y_i

则，其对数概率密度函数 $l$_i(β),为
$l$_i(β)=y_ilogG(x_iβ)+(1-y_i)log[1-G(x_iβ)]

最终得到对数似然函数为
L(β)=Σ $l$_i(β)，(i=1,2,…,m)
根据KKT条件,对L(β)求极值，即求得参数β_i
(上述中，x与β均代表向量，且向量长度为n+1)

这里说的只是对参数的点估计，还有(置信)区间估计省略了.

备注：Logistics回归模型估计的假设条件

• 数据来源于随机样本；
• 对多元共线性敏感；
• 因变量只能取0或1；
• 不需要假定同分布和方差齐性(OLS估计中需要该假定)；
• 不需要假定变量之间存在多元正态分布，如果存在会增加模型的功效及求解的稳定性(Tabachnick & Fidell 1996).(OLS估计中需要假定变量服从多元正态分布)

7，模型的假设检验与筛选：

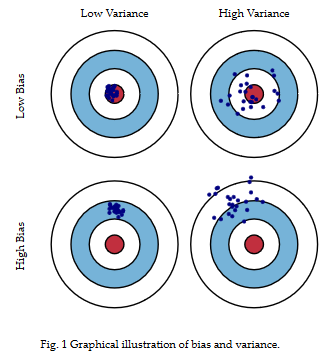
哪里有模型，哪里就需要有Bias-variance tradeoff原则。

从上图中的公式与说明中，我们知道均方误差可以分解成：
Error = Bias + Variance + Noise
Error反映的是整个模型的准确度，被拆解为两个重要部分(噪声先不考虑)。Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是如果可以重复建模的过程，生成多个模型，则模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性或泛化能力。在一个实际系统中，Bias与Variance往往是不能兼得的。如果要降低模型的Bias，就一定程度上会提高模型的Variance，反之亦然。

在统计学习中：一般采用抽样，逐步回归、假设检验、以及类似于AIC的统计指标等方法来平衡bias+variance。

在机器学习中：一般用到k折交叉验证(K-fold Cross Validation)，以及正则化项(Regularization)一起来平衡bias+variance。当然还有bagging以及boosting的方法，bagging主要是减小了variance，boosting主要是减小bias。

总的来说，统计学习更注重中间过程，对模型生成的机理有很好的假设，也有比较完整的假设检验、模型筛选的方法。而机器学习更注重结果，模型的好坏也基本由最终预测结果来衡量，所以对模型原假设以及假设检验的方法并不是那么关心。因为机器学习的模型筛选方法都融合到了参数求解算法中了，即结构风险最小化—损失函数+正则化。

所以本文只先以logistics模型为例，介绍一些统计假设检验的方法来说明统计学习中如何对模型进行筛选与评价。对于机器学习的模型筛选与评价方法会放到算法中去讲解。

7.1 显著性检验

一般线性模型中，我们有t检验，F检验，用来判断模型参数的显著性。模型参数的显著性，即用来确定自变量(可能是单个自变量也可能是联合的自变量)是否对因变量有显著性影响的过程。

F检验原假设 $\beta_1=\beta_2=...=\beta_n=0$，用来判断我们的因变量是否显著性的依赖于至少一个 $x_i$.

t检验原假设 $\beta_i=0$，当通过F检验时，还需对每一个自变量进行检验，判断是否哪个自变量对因变量没有显著性的影响关系。

然而在logistic回归中，对单个系数的检验通常用到Wald检验或似然比检验。而对一组系数的检验通常用到似然比检验。

单个自变量系数绝对值很大时，对wald检验会有影响，因此应用用似然比检验查看。

(1) Wald检验

(2) 似然比/偏差(Deviance)检验
观测值与预测值的比较还可以用似然比检验(LRT)。

假设检验的核心问题是构造合理的统计量，而统计量的构造是非常困难的。为了解决此问题，尼曼和皮尔逊于1982年提出了"似然比"方法，利用此法可以解决构造统计量的困难。

但是LRT只对层级嵌套的模型之间的比较才有效，举个例子，一个模型M1自变量是X1,X2,X3，另一个模型M2自变量是X2,X3，那么我们就说M2嵌套在M1中。

LRT的统计量公式：D(deviance) = 2 $(lnL_f-lnL_s)$= $-2ln(\frac{L_s}{L_f})$
其中 $L_f$为复杂模型的最大似然值，通常以饱和模型(full or saturated model)为准； $L_s$为设定的简单模型的最大似然值。D统计量被称为偏差，近似的符合卡方分布。

首先，在层级嵌套的模型下，拥有更多自变量的复杂模型的对数似然值 $L_f$一定大于相对简单的模型的对数似然值 $L_s$。

当 $lnL_f$ 值显著大于 $lnL_s$ 值时， $\frac{L_s}{L_f}$即为小于1的分数，取对数后为负数，再乘以-2后，D值就会变成比较大的正值，表示两模型间相差的自变量对该样本数据有更好的解释性；

相反， $lnL_s$ 值近似于 $lnL_f$ 值时，D值就会很小接近于零，表示所设定的模型拟合很好；

为了检验两个模型似然值的差异是否显著，我们必须要考虑自由度。LRT检验中，自由度等于在复杂模型中增加的模型参数的数目。这样根据卡方分布临界值表，我们就可以判断模型差异是否显著。

备注：多元线性模型中，通常用F检验来检验出常数项外所有系数均为0的原假设。Logistics回归中，似然比检验服务于 同一目的。

(3) Hosmer-Lemeshow拟合优度检验(HL)
当自变量数据增加时，尤其是大量数值型的自变量，则每种自变量组合生成的不同条件下的观察案例会变得非常稀疏。使得D与pearson卡方检验不再适用于估计Logistics模型的拟合优度。为了克服该缺点，HL会根据预测概率值将数据分成大致的相同规模的10个组。将观测概率按其预测概率做升序排列，第一组包括预测概率最小的那些观测案例，而最后一组包括预测概率最大的那些观测案例。

HL符号G-2的自由度的卡方分布，卡方检验不显著表示模型拟合数据好，相反表示拟合的不好。

7.2 拟合优度—模型筛选/变量选择

虽然通过显著性检验，但一定有些自变量对因变量的影响大，有些影响小。再我们不断尝试变更变量选择的时候就会产生多个模型—如，采取逐步回归时。那么如何从众多模型中选择一个最优的呢？下面提供了几种参考方法。

(1) pearson 卡方拟合优度检验
模型估计完成以后，需要评价模型的预测值与实际值之间的匹配程度，以此来说明模型拟合优度的好坏。
pearson 卡方检验： $X^2=\sum_1^m \frac{O_j-E_j}{E_j}$

卡方统计量很小意味着预测值与观测值没有显著差异，表示这一模型很好的拟合了数据。

(2) 信息测量指标

$AIC=（\frac{-2LL_s + 2(K+S)}{n}）$

其中，K为模型中自变量的数目；S为变量类别总数-1(对于二分类的回归，总有S=2-1=1)；n是观测数量； $LL_s$是所设模型的估计最大似然值的自然对数。在其他条件不变的情况下，AIC越小表示模型拟合数据越好。AIC还常常应用于比较不同样本的模型，或应用于非嵌套关系的模型(非嵌套模型不能用LRT).

备注：有软件中的AIC公式为 $AIC=-2LL_s + 2(K+S)$，调整的 $-2LL_s$没有被观测数n所除。所以，它不能视为针对每个观测对 $-2LL_s$的调整所做的贡献。因此，这种定义下，只能用于比较对同一数据的不同模型。

另一种对AIC的改进指标是SC：

$SC=-2LL_s + (K+S)×ln(n)$

同样，SC也只能用于比较对同一数据所设的不同模型。

还有一种贝叶斯信息标准BIC：

$BIC=-2LL_s + d.f._s × ln(n)$

其中， $d.f._s=n-k-1$为模型的自由度，它等于样本规模与模型估计系数数目只差。饱和模型的BIC=0，当BIC>0,说明所设模型比饱和模型差，而BIC<0，说明饱和模型包括了太多的自变量，所设模型更好。

(3) 类 $R^2$指标
线性回归中， $R^2$的值有着十分诱人的解释特性，它描述了因变量的变动中由模型的自变量所"解释"的百分比。但是Logistics模型中，却没有相应的统计指标。不过，可以在似然值对数的基础上，构造类似于 $R^2$的指标。如， 似然比指数（LRI, Green 1900; Hosmer and Lemeshow 1989）.

将 $-2LL_0$(零模型的最大似然值对数)类比于线下回归模型中的总平方和TSS，将 $-2LL_s$(所设模型最大似然值对数)类比于误差平方和ESS。于是，
LRI=( $\frac{-2LL_0-(-2LL_s)}{-2LL_0}$)

8，模型诊断—样本数据不满足模型假设时

完成建模后还需对模型进行一些诊断，通用的诊断要检验模型有无共线性、异方差的问题。对于logistic模型，也有其自身的一些问题。大都是数据结构的问题，因变量数据结构问题可能导致过离散、特异值；自变量数据结构问题可能导致空单元、完全分离、共线性等。

(1) 空单元(zero cell count)
这个问题相对比较简单，即根据因变量构建的交互表中，对应的观测频数为0。空单元问题主要发生在分类变量，可以通过合并类型来消灭空单元问题。

空单元通常会导致无法收敛，或模型有很大的估计系数和特别大的系数估计标准误。

(2) 完全分离

(3) 共线性
同线性回归一样，logistic回归也对自变量中存在多元共线性很敏感。
共线性将导致系数估计的标准误差增加。同样，可以通过自变量的相关阵进行诊断。或者用通用的VIF来进行诊断。

(4) 过离散
如果发生反应变量的测量方程超过名义上的方差 $n_j p_j(1-p_j)$，就称这种现象为过二项变异(extra binomial variation)或过离散。

实际数据中常有过离散现象，如果反应概率 $p_j$并不是随机变化，那么 $p_j$的变动将会造成 $y_j$的方差大于其本来应有的方差。

通常采用卡方或Deviance统计量来估计离散统计量。离散参数估计为卡方或Deviance统计量除以相应的自由度。

(5) 特异值和杠杆点
在logistic回归中，如果一个案例的实际结果是一种类型而其预测值却在另一类型上有很高的概率，便认为是特异值。

通常通过杠杆度、Cook距离等筛选出对参数估计以及预测值有很大影响的案例。

二，算法

求解Logistic模型的算法有梯度上升法，牛顿法或拟牛顿法，迭代尺度法等。本文只会介绍梯度上升以及牛顿法，其他的方法会放到最优化理论的章节中去介绍。

仍然假设自变量x的个数为n个，加上常数项x₀=1的扩展，x向量的长度为n+1，同时假定样本量为m个。于是，我们的目标就是在给定y₁,y₂,…,y_m个样本值下，求解β₀,β₁,…,β_n。

1，梯度上升法
根据上述讨论可知logistic模型的对数似然函数为

L(β)=Σ $l$_i(β)
=Σ[y_ilogG(x_iβ_i)+(1-y_i)log(1-G(x_iβ_i))]
=Σ[y_ilog $\frac{exp(xβ)}{1+exp(xβ)}$+(1-y_i)log(1- $\frac{exp(xβ)}{1+exp(xβ)}$)]
=Σ[ y_i(xβ)-log(1+exp(xβ)) ]

对对数似然函数L(β)求导，得到每个β_j的更新公式
(j=1,2,…,n)

$\frac{∂L(β)}{∂β_j}$= $\sum_1^m${x_ij(y_i - $\frac{exp(x_iβ_i)}{1+exp(x_iβ_i)})$}

则，梯度上升法的更新公式为：
β_j : β_j + $\alpha$ $\frac{∂L(β)}{∂β_j}$
β_j : β_j + $\alpha$ $\sum_1^m${x_ij(y_i - $\frac{exp(x_iβ_i)}{1+exp(x_iβ_i)})$}
(因为求最大值，此时为梯度上升)

先初始化随机设置参数值β_i,可以全为零或者全随机。 然后根据更新公式，更新参数迭代到指定精度为止，其中 $\alpha$表示梯度方向上的搜索步长。

2，牛顿法
上面提到过的梯度上升法是一阶收敛,接下来要讲的牛顿法是在其基础上进行的二阶收敛的方法，所以实际中牛顿法比梯度上升法更快。牛顿法适用于logistic模型或广义线性模型的求解。

那么什么是牛顿法呢？可以从几何图形上理解，也可以从泰勒展开的角度上理解。

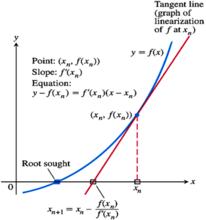
几何角度，如下图：

假设，如图蓝线代表的目标方程为y=f(x)，我们想求解f(x)=0的解。那么我们会利用x_n点的切线L与x轴交点的横坐标x_n+1来作为一次逼近，当f(x)=0时，停止更新，对应的x值即为所求。

泰勒展开角度：

综上，我们可以用牛顿法得到求解f(x)=0的更新公式：
x: x - $\frac{f(x)}{f(x)&#x27;}$

我们再回到logistics回归的求解问题，看看牛顿法是如何求解logistics回归参数的。因为我们需要求得极大似然估计，所以，必然是以一阶偏导均为零为必要条件的。于是，结合刚才讲的牛顿法，当我们的目标是求解f(x)’=0时，则更新公式变为：
x: x - $\frac{f(x)&#x27;}{f(x)&#x27;&#x27;}$

让我们回顾Logistic回归的对数似然函数的一阶偏导数：
$\frac{∂L(β)}{∂β_j}$= $\sum_1^m${x_ij(y_i - $\frac{exp(x_iβ)}{1+exp(x_iβ)})$}

β_j即是上述更新公式中的x， $\frac{∂L(β)}{∂β_j}$即是对应的一阶偏导f’(x)，代入即可使用牛顿法求解回归参数。
(使用这个方法需要f满足一定条件，参考牛顿法的一般化)

牛顿法的一般化：

如何让计算机快速的求解二阶导数，我们引入Hessian矩阵:
H=X^TAX，其中，X与A分别如下：

令对数似然函数的一阶偏导数方程的矩阵表示如下：

(其中， $\pi(x_i)$= $\frac{exp(x_iβ_i)}{1+exp(x_iβ_i)}$)

Hessian矩阵描述了多元函数的局部曲率（回想：一阶导为0，二阶导小于0，则存在极大值。Hessian矩阵是多元函数的二阶偏导数构成的方阵，所以其作用是描述局部曲率）。有了这个Hessian矩阵，我们就可以用牛顿迭代法继续进行计算了。

我们根据Hessian矩阵可以判断3种情况：
(1) 如果H(M)是正定矩阵，则临界点M处是一个局部极小值
(2) 如果H(M)是负定矩阵，则临界点M处是一个局部极大值
(3) 如果H(M)是不定矩阵，则临界点M处不是极值

如何判断H是正定还是负定的呢？
因为我们已经把Hessian矩阵拆分成二次型：H=X^TAX，所以我们可以根据下面的等价条件进行判断：
“正定二次型的充要条件是的矩阵的特征值全大于零。为负定二次型的充要条
件是的矩阵的特征值全小于零，否则是不定的。”

对于logistics回归，因为矩阵A中 $\pi(x_i)$-1一定是小于零的，所以H负定，一定存在(局部)极大值。
所以，其更新公式为：

β：β - H^-1U

(上述公式的意义就是，用一个一阶导数的向量乘以一个二阶导数矩阵的逆，实质上数矩阵形式 $f&#x27;(x)/f&#x27;&#x27;(x)$)

Hessian矩阵H是对称负定的，将矩阵A提取一个负号出来，得到A’

然后Hessian矩阵H变为H’=X^TA’X，那么牛顿更新公式也变为：
β： β + H’^-1 U
求解H’^-1时，由于H’是对称正定的，可以用Cholesky矩阵分解法来解。

三，案例分析

R语言

library("MASS")
library("ggplot2")

##加载MASS里面的一个数据包并查看数据结构
data(menarche);
str(menarche);summary(menarche)
##ggplot2快速画图,查看散点图的分布
p=qplot(Age,Menarche/Total,data=menarche);p

##用glm构建logit模型
##cbind是生成矩阵一列是“1”成功的样本量，一列是“0”失败的样本量作为自变量矩阵
##自变量也可以直接用类标签形式的“1”/“0”的一维向量来取代cbind(...)的位置
glm.logit = glm(cbind(Menarche, Total-Menarche) ~ Age,
              family=binomial(logit), data=menarche)

##结合样本散点图,查看logti模型的拟合曲线
##产生了warning,可以先合并原数据框与拟合出的概率的数据,data=合并后的数据框即可避免，se是设置是否在图中显示置信区间。
p+stat_smooth(aes(x=menarche$Age, y=glm.logit$fitted), method="glm", family="binomial",se=F,color="red")


##如果不用ggplot2,也可以使用R原生的方法
plot(Menarche/Total ~ Age, data=menarche)
lines(menarche$Age, glm.logit$fitted, type="l", col="red")
title(main="Menarche Data with Fitted Logistic Regression Line")

##查看logit模型的估计结果
summary(glm.logit)
##解释:
##Null Deviance = 2(LL(Saturated Model) - LL(Null Model))
##Residual Deviance = 2(LL(Saturated Model) - LL(Proposed Model)) 
##Null Model 假设模型只有常数项
##Saturated Model 假设模型有n个变量
##Proposed Model 你自己假定的模型
##详细参考上文中讲解的偏差

##似然比检验,上文中有讲过似然比检验的方法
##原假设是:复杂模型比其简单的嵌套模型多的对应的自变量系数=0
##p-value = 1-pchisq(残差的改变量,自由的的改变量)

##例如:summary(logit_model)得到下面的值
##Null deviance: 958.66  on 51  degrees of freedom
##Residual deviance: 198.63  on 42  degrees of freedom
##则,pchisq(958.66-198.63, 9)≈1
##1-pchisq=0<0.05拒绝原假设,说明该自变量有显著性影响

##如果存在很多的连续变量，还需要做HL检验
library(sjmisc)
HL_test <- hoslem_gof(x = model)
HL_test

##模型筛选时用到的一些方法
anova(glm.logit, test="Chisq")
drop1(glm.logit, test="Chisq")

---

下一节：第3章-从线性概率模型到广义线性模型(2)

---

参考：
1，计量经济学导论-J.M伍德里茨，第七章与第十七章
2，统计学习-李航，第六章
3，机器学习公开课-Andrew Ng
4，https://en.wikipedia.org/wiki/Gradient_descent
5，http://www.zhihu.com/question/19723347
6，http://blog.csdn.net/acdreamers/article/details/44658249
7，http://baike.baidu.com/link?url=vygc1zboVevA_qUXoRBEOpfVgz4PnbCKik8E2V0aP8i42DnSnAKs4GtGJA3ppH4shPUrsiB_7UOUZoolOee6la
8，http://ww2.coastal.edu/kingw/statistics/R-tutorials/logistic.html
9，http://scott.fortmann-roe.com/docs/BiasVariance.html
10，http://nlp.stanford.edu/~manning/courses/ling289/logistic.pdf
11，http://stackoverflow.com/questions/9258708/plot-two-curves-in-logistic-regression-in-r
12，http://cos.name/2015/08/some-basic-ideas-and-methods-of-model-selection/
13，Logistics回归模型-方法与应用-王济川，郭志刚