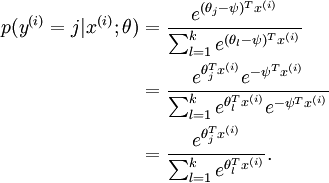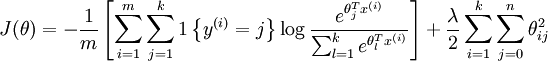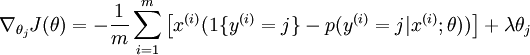广义线性模型与指数分布族的理解

在机器学习领域，很多模型都是属于广义线性模型（Generalized Linear Model, GLM），如线性回归，逻辑回归，Softmax回归等。

广义线性模型有3个基本假设:

（1） 样本观测值 $y_i$满足带参数 $\eta$的指数分布族。即GLM是基于指数分布族的，所以我们先来看一下指数分布族的一般形式：
$p(y;\eta)=b(y)exp(\eta^TT(y)-a(\eta))$

其中， $\eta$ 为自然参数，在一般情况下， $\eta$为实数（多项式分布中 $\eta$为向量）。 $T(y)$为充分统计量（一般情况下，如高斯分布和伯努利分布中， $T(y)=y$）。 $a(\eta)$为累积量函数。给定 $T,a,b$, 通过参数 $\eta$ ，我们可以得到指数分布族中的各类分布。

进一步解释下什么是充分统计量： $T(y)$是未知分布 $p$参数 $\theta$的充分统计量，当且仅当 $T(y)$能够提供 $\theta$的全部信息。比如在正态分布中，样本均值和方差就是未知的正态分布的充分统计量，因为这两个参数可以完全描述整个样本的分布特性。

对于假设1，换句话说：给定 $x,\theta$, 输出 $y$ 满足参数为 $\eta$的指数族分布。

（2） 分布模型参数 $\eta$与输入样本 $x$呈线性关系，即 $\eta=\theta^{T}x$。(当 $\eta$为变量时， $\eta_i=\theta_i^Tx$）

（3） $h(x)=E[y|x]$(线性回归和逻辑回归都满足该式，例如逻辑回归中， $h(x)=p(y=1|x;\theta)$,数学期望 $E[y|x]=1*p(y=1|x;\theta)+0*p(y=0|x;\theta)$，因此 $h(x)=E[y|x]$)

接下来，我们首先证明高斯分布、伯努利分布和多项式分布属于指数分布族，然后我们由广义线性模型推导出线性回归，逻辑回归和多项式回归。这是因为：线性回归假设样本和噪声服从高斯分布，逻辑回归假设样本服从伯努利分布，多项式回归假设样本服从多项式分布。

注:关于多项式回归，会介绍得稍微详细点。

一、证明分布属于指数分布族

1.1 证明高斯分布属于指数分布族

因为方差 $\sigma^2$项对我们最终求 $\theta$和 $h_\theta(x)$没有影响，，因此为了简化计算，我们令 $\sigma=1$:

$\begin{aligned} p(y;u)&={1\over \sqrt{2\pi}\sigma}exp(-{(y-u)^2\over 2\sigma^2})\\ &= {1\over \sqrt{2\pi}}exp(-{(y-u)^2\over 2})\\ &={1\over \sqrt{2\pi}}exp(-{1\over 2}y^2)*exp(uy-{1\over 2}u^2) \end{aligned}$

因此：
$\begin{aligned} b(y)&={1\over \sqrt{2\pi}}exp(-{1\over 2}y^2)\\ \eta&=u \\ T(y) &=y\\ a(\eta)&={1\over 2}u^2 ={1\over 2}\eta^2 \end{aligned}$

由以上分析，我们可以得到结论：高斯分布属于指数分布族的一类。

1.2 证明伯努利分布属于指数分布族

$\begin{aligned} p(y;\phi)&=\phi^y(1-\phi)^{1-y}\\ &= exp(ylog\phi+(1-y)log(1-\phi))\\ &=exp(ylog{\phi\over 1-\phi}+log(1-\phi)) \end{aligned}$

因此：
$\begin{aligned} b(y)&=1\\ \eta&=log{\phi\over 1-\phi} \\ T(y) &=y\\ a(\eta)&=-log(1-\phi)=log(e^\eta+1) \end{aligned}$

由以上分析，我们可以得到结论：伯努利分布属于指数分布族的一类。

同时，由 $\eta=log{\phi\over 1-\phi}$可以得到 $\phi={1\over 1+e^{-\eta}}$，这就是我们熟悉的sigmoid函数。 同时根据第2个假设中的 $\eta=\theta^{T}x$,则 $\eta=log(\frac{\phi}{1-\phi})=\theta^{T}x$

1.3 证明多项式分布属于指数分布族

Softmax回归本质上是一个多分类问题。假设输出 $y$ 有 $k$类，即 $y\epsilon [1,2,...,k]$。我们对多项式回归输出的 $k$个可能值参数化: $\phi_1,\phi_2,...,\phi_k$表示每个输出值的概率大小。当然，因为概率和为1，所以这么多个参数是冗余的，即其中一个参数可以由其他所有参数推导出来，比如 $\phi_k = 1-\sum_{i=1}^{k-1}\phi_i$。
我们定义 $T(y)\epsilon R^{k-1}$为以下表达式：

$T(1)=\begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots\\ 0 \end{bmatrix},T(2)=\begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots\\ 0 \end{bmatrix},T(3)=\begin{bmatrix} 0 \\ 0 \\ 1 \\ \vdots\\ 0 \end{bmatrix},...,T(k-1)=\begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots\\ 1 \end{bmatrix},T(k)=\begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots\\ 0 \end{bmatrix}$

我们可以看到， $T(y)$ 是一个 $k−1$ 维的向量，而不是一个实数。我们定义 $(T(y))_i$ 为 $T(y)$ 的第 $i$ 个元素。

为了方便表示，我们使用 $1\{.\}$作为指示性函数，当括号里的值为真时， $1\{.\}=1$否则 $1\{.\}=0$。比如： $1\{2=3\}=0$ ， $1\{3=4-1\}=1$。根据以上定义，我们可以得到下式： $(T(y))_i=1\{y=i\}$,且 $E[(T(y))_i]=p(y=i)=\phi_i.$

多项式分布：
$\begin{aligned} p(y|x;\theta)&=\phi_1^{1\{y=1\}}\phi_2^{1\{y=2\}}...\phi_k^{1\{y=k\}}\\ &=\phi_1^{1\{y=1\}}\phi_2^{1\{y=2\}}...\phi_k^{1-\sum_{i=1}^{k-1}1\{y=i\}}\\ &=\phi_1^{(T(y))_1}\phi_2^{(T(y))_2}...\phi_k^{1-\sum_{i=1}^{k-1}(T(y))_i}\\ &=exp((T(y))_1log\phi_1+(T(y))_2log\phi_2+...+(1-\sum_{i=1}^{k-1}(T(y))_i)log\phi_k)\\ &=exp((T(y))_1log{\phi_1\over \phi_k}+(T(y))_2log{\phi_2\over \phi_k}+...+(T(y))_{k-1}log{\phi_{k-1}\over \phi_k}+log\phi_k) \end{aligned}$

因此：
$\begin{aligned} b(y)&=1\\ \eta&=\begin{bmatrix}log{\phi_1\over \phi_k}\\ log{\phi_2\over \phi_k}\\ \vdots\\ log{\phi_{k-1}\over \phi_k} \end{bmatrix}\\ T(y) &=\begin{bmatrix}(T(y))_1\\ (T(y))_2\\ \vdots\\ (T(y))_{k-1} \end{bmatrix}\\ a(\eta)&=-log(\phi_k) \end{aligned}$

由以上分析可得到，多项式分布属于指数分布族的一类。
而且，对于类别 $i$,有 $\eta_i=log{\phi_i\over \phi_k}$，所以 $\phi_i=\phi_ke^{\eta_i}$ ，累加所有类别的概率为1，即： $\sum_{i=1}^k\phi_i=\sum_{i=1}^k\phi_ke^{\eta_i}=1$，所以 $\phi_k={1\over \sum_{i=1}^ke^{\eta_i}}$，因此 $\phi_i={e^{\eta_i}\over \sum_{j=1}^ke^{\eta_j}}$，这便是softmax函数的由来。

二、由GLM推导出分布

2.1 由广义线性模型推导出线性回归

我们知道，在线性回归中 $y|x;\theta-N(\mu,\sigma^2)$，即输出 $y$ 满足均值为 $\mu$ 的高斯分布;由广义线性模型得到：
$\begin{aligned} h_\theta(x)&=E[y|x]\\ &= \mu\\ &=\eta\\ &=\theta^Tx \end{aligned}$

其中，第一个等式由假设3得到，第二个等式是高斯分布的数学期望，第三个等式由假设1得到，即由高斯分布属于指数分布族推导出来，第四个等式由假设2得到。

2.2 由广义线性模型推导出逻辑回归

我们知道，在逻辑回归中， $y|x;\theta-Bernoulli(\phi)$，其中 $\phi=p(y=1|x;\theta)$，即输出 $y$满足伯努利分布;由广义线性模型得到：
$\begin{aligned} h_\theta(x)&=E[y|x]\\ &= p(y=1|x;\theta)\\ &=\phi\\ &={1\over 1+e^{-\eta}} \\ &={1\over 1+e^{-\theta^Tx}} \end{aligned}$

其中，第一个等式由假设3得到，第二个等式是高斯分布的数学期望，第三个等式是我们的定义，第四个等式由假设1得到，即由伯努利分布属于指数分布族推导出来，第五个等式由假设2得到。

2.3 由广义线性模型推导出多项式回归

在多项式回归中预测输出值：
$\begin{aligned} h_\theta(x)&=E[y|x]\\ &=\begin{bmatrix} 1\{y=1\}|x;\theta\\ 1\{y=2\}|x;\theta\\ \vdots\\ 1\{y=k-1\}|x;\theta \end{bmatrix}\\ &=\begin{bmatrix} \phi_1\\ \phi_2\\ \vdots\\ \phi_{k-1} \end{bmatrix}\\ &=\begin{bmatrix} {exp(\theta_1^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)}\\ {exp(\theta_2^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)}\\ \vdots\\ {exp(\theta_{k-1}^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)} \end{bmatrix} \end{aligned}$
输出值为每个类别的概率，且 $p(y=k|x;\theta)=1-\sum_{i=1}^{k-1}p(y=i|x;\theta)$

2.3.1 多项式回归中求解参数

接下来，我们来看一下多项式回归中如何求解参数：
与逻辑回归中利用最大似然估计求解一样，在这里我们也用最大似然估计（就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者什么样的参数才能使我们观测到目前这组数据的概率最大） 。

即：对数似然函数为：
$\begin{aligned} J(\theta)&=log\prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta)\\ &=\sum_{i=1}^mlog \ p(y^{(i)}|x^{(i)};\theta)\\ &=\sum_{i=1}^mlog \ \phi_1^{1\{y^{(i)}=1\}}\phi_2^{1\{y^{(i)}=2\}}...\phi_k^{1\{y^{(i)}=k\}}\\ &=\sum_{i=1}^m{1\{y^{(i)}=1\}}log \ \phi_1+{1\{y^{(i)}=2\}}log \ \phi_2+...+{1\{y^{(i)}=k\}}log \ \phi_k\\ &=\sum_{i=1}^m{1\{y^{(i)}=1\}}log \ {exp(\theta_1^Tx^{(i)})\over \sum_{j=1}^kexp(\theta_j^Tx^{(i)})}+{1\{y^{(i)}=2\}}log \ {exp(\theta_2^Tx^{(i)})\over \sum_{j=1}^kexp(\theta_j^Tx^{(i)})}+...+{1\{y^{(i)}=k\}}log \ {exp(\theta_k^Tx^{(i)})\over \sum_{j=1}^kexp(\theta_j^Tx^{(i)})}\\ &=\sum_{i=1}^m(1\{y^{(i)}=1\}log \ e^{\theta_1^Tx^{(i)}}+1\{y^{(i)}=2\}log \ e^{\theta_2^Tx^{(i)}}+...+1\{y^{(i)}=k\}log \ e^{\theta_k^Tx^{(i)}}-log\sum_{j=1}^ke^{\theta_j^Tx}) \end{aligned}$

最后一步中，为什么只有一个 $log\sum_{j=1}^ke^{\theta_j^Tx}$是因为只能有一个指数函数 $1\{.\}$成立。
对类别 $l$的参数求导：
$\begin{aligned} {\partial J(\theta)\over \partial \theta_j}&=\sum_{i=1}^m(1\{y^{(i)}=l\}*x^{(i)}-{1\over \sum_{j=1}^kexp(\theta_j^Tx^{(i)})}*exp(\theta_l^Tx)*x^{(i)})\\ &=\sum_{i=1}^m(1\{y^{(i)}=l\}*x^{(i)}-p(y^{(i)}=l|x^{(i)};\theta)*x^{(i)}) \end{aligned}$

注意： ${\partial J(\theta)\over \partial \theta_j}$只是针对一个类别所做的偏导，我们还需要继续对类别的每个参数做偏导，最后对所有类别执行相同求导操作，这样才算完整地完成参数优化的一次迭代。接着，使用梯度上升法不断迭代，直到收敛。

最后，我们的预测输出值的表达式如下：
$\begin{aligned} h_\theta(x) &=&\begin{bmatrix} {exp(\theta_1^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)}\\ {exp(\theta_2^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)}\\ \vdots\\ {exp(\theta_{k-1}^Tx)\over \sum_{j=1}^kexp(\theta_j^Tx)} \end{bmatrix} \end{aligned}$

取 $h_\theta(x)$中概率最大的那一项作为输出值。例如：假设预测样本预测值为hθ(x)=[0.1,0,0.05,0.6,0.05,0.05,0.1,0.05,0,0]hθ(x)=[0.1,0,0.05,0.6,0.05,0.05,0.1,0.05,0,0] ,那么该测试样本被判定为4.

2.3.2 参数冗余问题

Softmax 回归有一个不寻常的特点：它有一个“冗余”的参数集。为了便于阐述这一特点，假设我们从参数向量 $\theta_j$中减去了向量 $\textstyle \psi$，这时，每一个 $\theta_j$ 都变成了 $\theta_j-\psi(j=1,2,...,k)$。此时假设函数变成了以下的式子：

换句话说，从 $\theta_j$中减去 $\textstyle \psi$完全不影响假设函数的预测结果！这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说， Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数，可以求出多组参数值，这些参数得到的是完全相同的假设函数 $h_\theta$。

进一步而言，如果参数 $(\theta_1, \theta_2,\ldots, \theta_k)$ 是代价函数 $J(\theta)$ 的极小值点，那么 $\textstyle (\theta_1 - \psi, \theta_2 - \psi,\ldots, \theta_k - \psi)$ 同样也是它的极小值点，其中 $\textstyle \psi$ 可以为任意向量。因此使 $\textstyle J(\theta)$ 最小化的解不是唯一的。

那么，应该如何解决这个问题呢？

我们通过添加一个权重衰减项 $\textstyle \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^{n} \theta_{ij}^2$ 来修改代价函数，这个衰减项会惩罚过大的参数值，现在我们的代价函数变为：

有了这个权重衰减项以后 ( $\textstyle \lambda > 0$)，代价函数就变成了严格的凸函数，这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵，并且因为 $\textstyle J(\theta)$是凸函数，梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。

为了使用优化算法，我们需要求得这个新函数 $\textstyle J(\theta)$ 的导数，如下：

通过最小化 $\textstyle J(\theta)$，我们就能实现一个可用的 softmax 回归模型。

2.3.3 Softmax 回归 vs. k 个二元分类器

如果你在开发一个音乐分类的应用，需要对 $k$种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 $k$ 个独立的二元分类器呢？

这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 $k = 4$ 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 $k$ 设为5。）

如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。

现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？

在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。

参考文献

【1】广义线性模型与指数分布族
【2】机器学习（二）广义线性模型：逻辑回归与Softmax分类
【3】机器学习算法系列（24）：机器学习中的损失函数
【4】Softmax回归