数据学习(2)·广义线性模型

作者课堂笔记，有问题请联系[email protected]

1 指数族

如果一种分布可以写成如下形式，那么这种分布属于指数族：
$p(y;\eta)=b(y)e^{\eta^{T}T(y)-a(\eta)}$

$\eta:$ 分布的自然参数
$T(y):$ 充分统计量
$a(\eta):log$ 的分隔函数( $a(\eta)$ 作为归一化常量，目的是让 $\sum_yp(y;\eta)=1$ )

1.1 伯努利分布

分布形式：
$p(y;\phi)=\phi^y(1-\phi)^{1-y}$

$\eta=log(\frac{\phi}{1-\phi})$
$b(y)=1$
$T(y)=y$
$a(\eta)=log(1+e^\eta)$

1.2 高斯分布

$y\sim\chi(\mu,1)$
$p(y;\theta)=\frac{1}{\sqrt{2\pi}}e^{-\frac{(y-\mu)^2}{2}}$

$\eta=\mu$
$b(y)=\frac{1}{\sqrt{2\pi}}e^{\frac{y^2}{2}}$
$T(y)=y$
$a(\eta)=\frac{1}{2}\eta^2$

$y\sim\chi(\mu,\sigma^2)$
$p(y;\theta)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(y-\mu)^2}{2\sigma^2}}$

$\eta=\begin{bmatrix}\frac{\mu}{\sigma^2}\\-\frac{1}{2\sigma^2}\end{bmatrix}$
$b(y)=\frac{1}{\sqrt{2\pi}}$
$T(y)=\begin{bmatrix}y\\y^2\end{bmatrix}$
$a(\eta)=\frac{\mu}{2\sigma^2}+log\sigma$

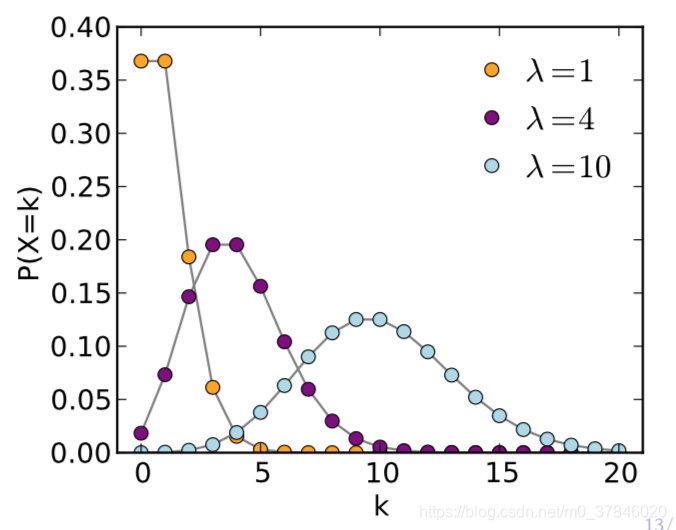
1.3 柏松分布

$p(y;\lambda)=\frac{\lambda^ye^{-\lambda}}{y!}$
lambda

$\eta=log(\lambda)$
$b(y)=\frac{1}{y!}$
$T(y)=y$
$a(\eta)=e^\eta$

2 广义线性模型

通过改变y的分布，从而更好的拟合数据。是一种构造线性模型的方法，其中Y|X来自于指数族。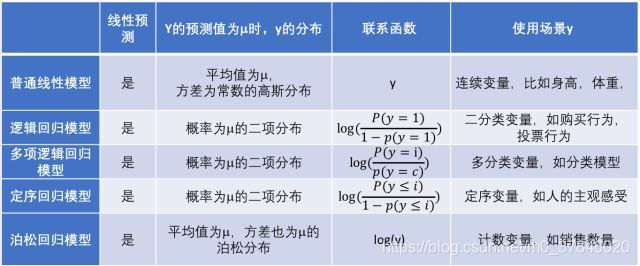 GLM

来源https://www.sohu.com/a/228212348_349736

广义线性模型的设计初衷：

为了使响应变量y可以有任意的分布。
允许任意的函数（链接函数）可以随着输入的x变化。

构建方法：

y|x; $\theta\sim$ 指数族分布（高斯、柏松、伯努利…）
我们的目标是给定x，预测T(y)的期望，大多数情况是T(y)=y,而在其他情况下可能是E[y|x; $\theta$ ]
自然参数 $\eta$ 和x是线性相关的，满足 $\eta=\theta^Tx$
如果问题满足以上的三个假设，那么我们那就可以构造广义线性模型来解决问题。

2.1 最小二乘法

应用GLM的构造准则：

y|x; $\theta\sim N(\mu,1)$
$\eta=\mu,T(y)=y$
推导假设函数：
$h_\theta(x)=E[y|x;\theta]=\mu=\eta$
应用线性模型 $\eta=\theta^Tx$
$h_\theta(x)=\eta=\theta^Tx$
典范响应函数： $\mu=g(\eta)=\eta$
典范链接函数： $\eta=g^{-1}(\mu)=\mu$

2.2 Logistic回归

应用GLM的构造准则：

y|x; $\theta\sim Bernoulli(\phi)$
$\eta=log(\frac{\phi}{1-\phi}),T(y)=y$
推导假设函数：
$h_\theta(x)=E[y|x;\theta]=\phi=\frac{1}{1+e^{-\eta}}$
应用线性模型 $\eta=\theta^Tx$
$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$
典范响应函数： $\phi=g(\eta)=sigmoid(\eta)$
典范链接函数： $\eta=g^{-1}(\phi)=logit(\phi)$

2.3 柏松回归（顾客预测）

应用GLM的构造准则：

y|x; $\theta\sim Poisson(\lambda)$
$\eta=log(\lambda),T(y)=y$
推导假设函数：
$h_\theta(x)=E[y|x;\theta]=\lambda=e^\eta$
应用线性模型 $\eta=\theta^Tx$
$h_\theta(x)=e^{\theta^Tx}$
典范响应函数： $\lambda=g(\eta)=e^\eta$
典范链接函数： $\eta=g^{-1}(\lambda)=log(\lambda)$

2.4 SoftMax回归

$p(y;\phi)=\prod_{i=1}^k\phi_i^{1\{y=i\}}$
$\phi_k=1-\sum_{i=1}^{k-1}\phi_i$

T(y)= $\begin{bmatrix}1\{y=1\}\\...\\1\{y=k-1\}\\\end{bmatrix}$
$\eta=\begin{bmatrix}log(\frac{\phi_1}{\phi_k})\\...\\log(\frac{\phi_{k-1}}{\phi_k})\\\end{bmatrix}$
b(y)=1
a( $\eta$ )= $-log(\phi_k)$

应用GLM的构造准则：

y|x; $\theta\sim Multinomial(\phi_1,....\phi_k)$
$\eta_i=log(\frac{\phi_i}{\phi_k}),T(y)=\begin{bmatrix}1\{y=1\}\\...\\1\{y=k-1\}\\\end{bmatrix}$
$\phi_i=\frac{e^{\eta_{i}}}{\sum_{j=1}^ke^{\eta_{j}}}$
推导假设函数：
$h_\theta(x)=E[T(y);\theta]=\begin{bmatrix}\phi_1\\...\\\phi_{k-1}\\\end{bmatrix}....=\phi_i=\frac{e^{\eta_{i}}}{\sum_{j=1}^ke^{\eta_{j}}}$
应用线性模型 $\eta=\theta_i^Tx$
$h_\theta(x)=\frac{1}{\sum_{j=1}^ke^{\eta_{j}}}\begin{bmatrix}e^{\theta_1^Tx}\\...\\e^{\theta_{k-1}^Tx}\\\end{bmatrix}$
典范响应函数： $\phi_i=g(\eta)=\frac{e^{\eta_{i}}}{\sum_{j=1}^ke^{\eta_{j}}}$
典范链接函数： $\eta=g^{-1}(\phi_i)=log(\frac{\phi_i}{\phi_k})$

3 总结广义线性模型

在这里插入图片描述

4 练习

答案地址：https://pan.baidu.com/s/1ytOYfFKUDKVJI7Yg-07KoA