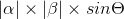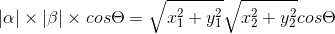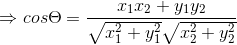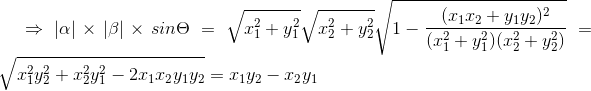版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/u010916338/article/details/85050793
上面矩阵所表示的几何意义就是求下图平行四边形的面积。
取出两个行向量(4,3)和(3,4),平移出如图所示的平行四边形。

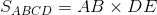
AB=5,DE未知
由向量点乘公式可得:
综上,由代入法可得二阶行列式是计算向量围成的平行四边形的面积。
一般推导公式如下:
如图令B(x1, y1), D(x2, y2)
即证明
则相当于已知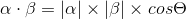
注:推倒过程未考虑符号问题,不影响整体理解
![$$ \left[ \begin{matrix} 4 & 3 \\ 3 & 4 \end{matrix} \right] \tag{3} $$ = 4\times 4 -3\times 3=7](https://img-blog.csdnimg.cn/20181217170553300)
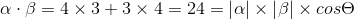
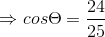
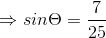
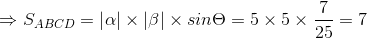
![$$ \left[ \begin{matrix} x_1 & y_1 \\ x_2 & y_2 \end{matrix} \right] \tag{3} $$ = S_{ABCD}](https://img-blog.csdnimg.cn/20181217170553400)