在此处输入标题

标签（空格分隔）：未分类

\[\sum_{i = 1}^ngcd(i,n) = \sum_d d\sum_{i = 1}^n(gcd(i,n) = d)\]
\[ = \sum_d d\sum_{i = 1}^{\frac{n}{i}}(gcd(i,\frac{n}{d}) = 1） = \sum_d d \phi(\frac{n}{d})\]

排列

对换，对于一个排列操作，对于一个偶排列一次对换之后变为奇排列
反之变为偶排列

行列式

N阶行列式室友N^2个数aij(i,j = 1,2,3,...n)

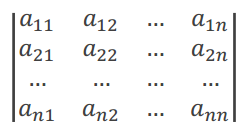
行列式的数=$\sum_ {j_1,j_2,....j_n}sgn(j_1j_2...j_n)a_{1j_1}a_{2j_2}...a_{nj_n}$
$sgn()对于排列的函数，若排列A为奇排列则，sgn(A) = -1,为偶排列，则sgn(A) = 1$
那么对于行列式的计算也就是从第一排走到最后一排的所有路径分别*路径标号排列的sgn函数，所有路径中不能有相同列的情况
(从每行选一个数使他的列不同)
下面式子的行列式值为18

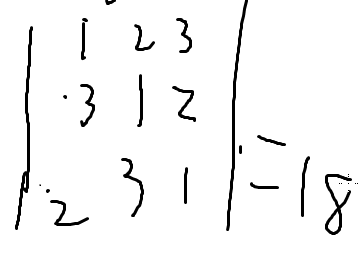
代码：

cin >> n;
for(int i = 1;i <= n;++ i) 
    for(int j = 1;i <= n;++ j) 
        z[i][j] = read(); 
for(int i = 1;i <= n;++ i) 
    y[i] = i; 
int ans = 0;
do { 
    int res =  1; 
    for(int i = 1;i <= n;++ i)
        for(int j = 1;j <= n;++ j) 
    if(jipailie(y)) res = res; 
    ans += ans;     
}while(next_premutation(y + 1,y + n + 1));

复杂度$O(n!*n)$

引理

由行列式的的计算定义式的到

引理1

行列互换，值不变
因为(从每行选一个数使他的列不同）等价于从每一列选一个数是他的列不同

引理2

用一个数乘以行列式的某一行，等于用这个数乘以整个行列式的值

引理3

如果行列式中的某一行是两组数之和，那么这个行列式的的值等价于
该行拆为两组数,其他行不变的两个行列式的和
！
乘法分配率

引理4

对换行列式中两行的位置，行列式值变为相反数
因为交换后奇排列变为偶排列，偶排列变为奇排列，sgn函数相反

引理5

若有两行对应成比例，则行列式的值为0
提出一行系数后对换，发现将两行对换数值互为相反数，但行列式的值应不变，则行列式的值为0

引理6

若把某一行*上一个数加到另一行则行列式的值不变
证：加上后根据引理3拆开，那么对于其中一个行列式，据引理3他的值为0

余子式

余子式:选取某行的一个数，把该行该列抹掉，剩余的行列式就是余子式
设行列式$D$
$|D| = \sum_{i = 1} ^ nD_{1i}*T_{1,i} * |D_{1i}的余子式|$
T为系数$(-1)^{i + 1}$//因为对于余子式的方案数一定，sgn函数便取决于i，j

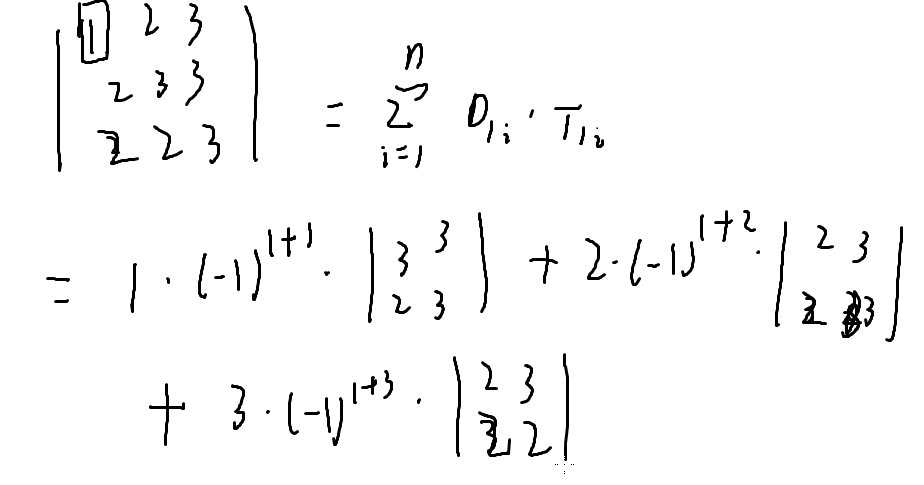
证明：考虑定义，在余子式中选择方案
那么我们就可以每次化为余子式计算行列式的值

Cramer法则

对与一组方程组的系数行列式$D$

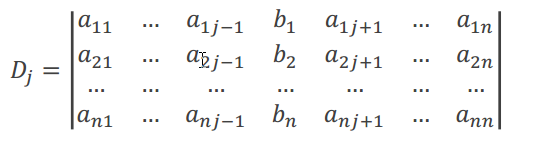
若行列式的值不为0
就可以把系数矩阵的每一列，分别用方程的值那一列替换掉
分别解出行列式的值，D(为系数行列式)，D1(表示方程解替换掉第一列)，D2....Dn
那么方程的解$X_i$为$ \frac{|D_i|}{|D|}$
简证：
对与第n列，那么我们对于第n列的每个系数*上X_n,对于前面的每一列i，前面的每一列i的值都成上X_i加到第n列上，这时第n行就变成了方程的值的那一列，且根据初等变换(引理6)，行列式值不变
然后我们就有了$O((n+1)!)$的解方程的方法了

高斯消元

咕咕咕

矩阵

定义

由nm个数构成的n行m列的数表
种类：

矩阵的相等：

就是相等啊

矩阵的加法

矩阵大小必须一样，对应位置相加，没了额

矩阵的减法

矩阵大小一样，对应位置相减，没了额

矩阵的数乘

矩阵的每个位置上的元素都乘上这个数

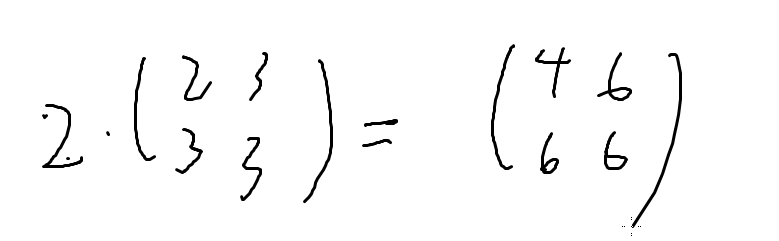
矩阵的乘法

设矩阵$A=(a_{ij})_{m*r},B=(b_{ij})_{r*k}$那么，$A*B=C(c_{ij})_{m*k}$
$c_{ij}=\sum_{k}a_{ik}*b_{kj}$

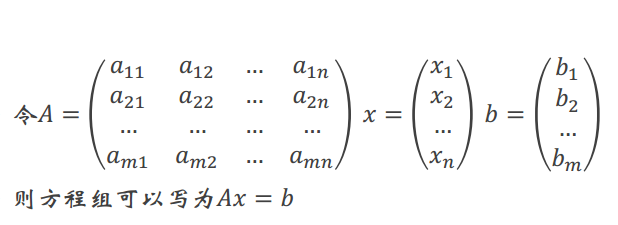
矩阵乘法的性质

逆矩阵

定义：

设A是n阶方针，若存在n阶方阵B使得AB=BA=I(单位矩阵)，则称A是可逆的(或者非奇异的)，B是A的一个逆矩阵。否则称A是不可逆的(或奇异的)

定理1：逆矩阵唯一

若B，C为A的逆矩阵，则B = C
AB = BA = I ， AC = CA = I -> B = C
证明： B = IB = CAB = C(AB) = CI = C

定理2：乘积后矩阵乘的行列式值为矩阵的行列式值相乘

定义det运算符
定理：设A,B为n阶方阵，则det(A,B)=det(A)det(B)
引理 : det(A1A2....As) = det(A1)det(A2)....det(As)
引理：det值不能互推逆矩阵的det乘积为det(I)<1>

求逆矩阵

1.待定系数法...可能可以吧
2.
A*矩阵就是吧A矩阵的每个位置都替换为它的代数余子式的值

插入一点逆矩阵的性质

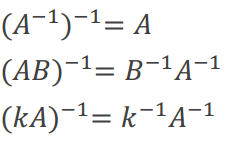
对于第二条的证明，只要证明他们乘起来是否=I

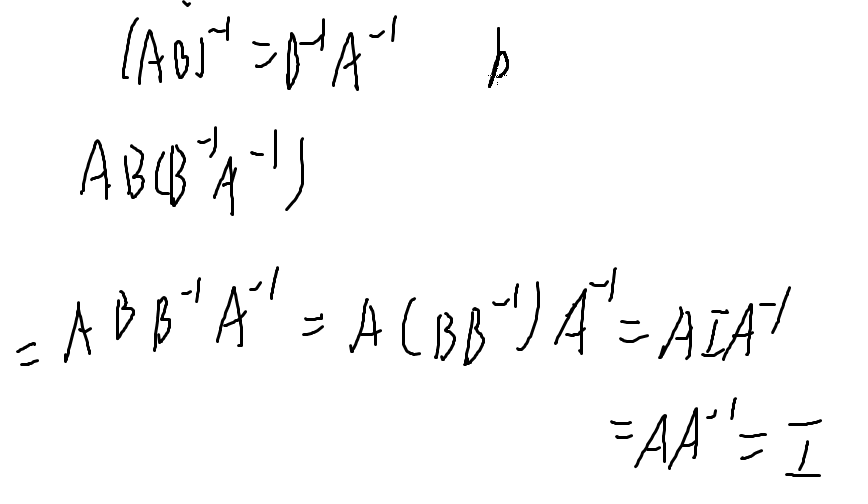
定理：设A为n阶方阵，若A可逆，则线性方程组Ax = b有唯
一解$X = A^{−1}b$
证明：

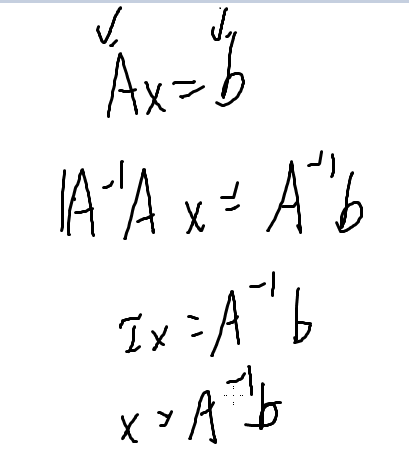
矩阵的初等变换

定义：矩阵的初等行（列）变换

1.用一个非零的数乘以某行
2.将某一行的x倍加到另一行
3.互换两行

定义初等矩阵

由初等矩阵I经过一次初等变换而来的矩阵
如下图，有三种(上方三种初等变换)

初等矩阵可逆

性质

定理：用初等矩阵B 左（右）乘矩阵A，相当于对矩阵A实行相应的初等行（列）变换
等价与对矩阵A做初等矩阵B所做的同样的初等变换

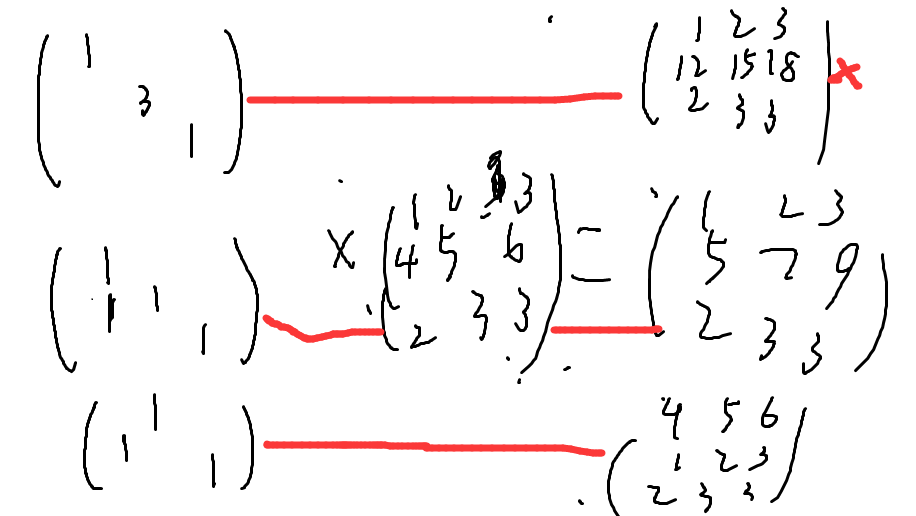
定义：
定义：若矩阵A可以由矩阵B经过一系列初等变换得到，则称
B与A相抵（等价），记做$A≅B$
相抵是一种等价关系，即$A≅B,A≅C;=>B≅C$

用初等变换求逆矩阵

若找到一系列初等矩阵$B_i$
使得$B_1B_2....B_i(A,I) = (I,A^{-1})$
那么${B_1B_2....B_i}$的乘积就是$A^{-1}$
考虑考斯消元的过程
对于矩阵A最后的被通过初等变换消成了只有对角线为1的矩阵$I$，那么那些初等变换的初等矩阵的乘积就是$A^{-1}$

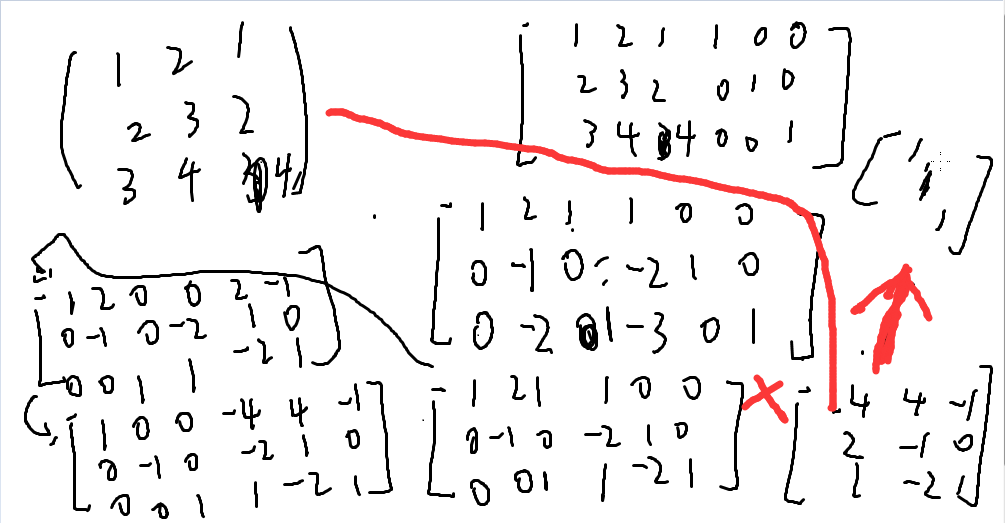
然后你就有了多项式算法求逆矩阵！复杂度$O(n^3)$

矩阵&行列式