通过上网搜索,找到一篇不错的讲解。
原文http://mdsa.51cto.com/art/201707/544991.htm
首先
文章讲解了面积的矢量表示方法:即两个矢量映射出面积大小。第一个矢量是(1.0),第二个矢量是(0,1),也就是说两个矢量分别是X轴和Y轴上的单位为正的单位向量,那么由这两个矢量构成的四边形,这个四边形其实就是一个正方形,根据面积的定义,其实就是宽=11=1。
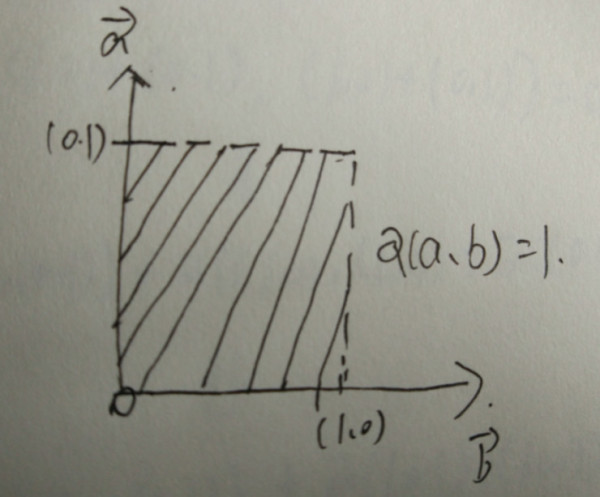
写成矢量表示就是
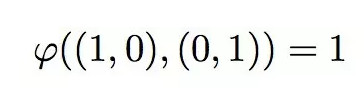
齐次性:
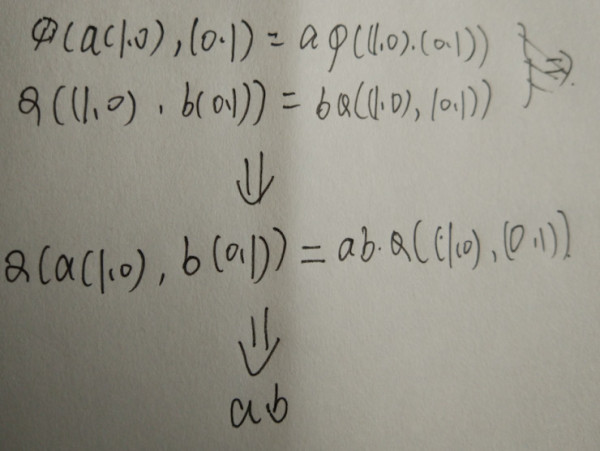
加法的线性映射:
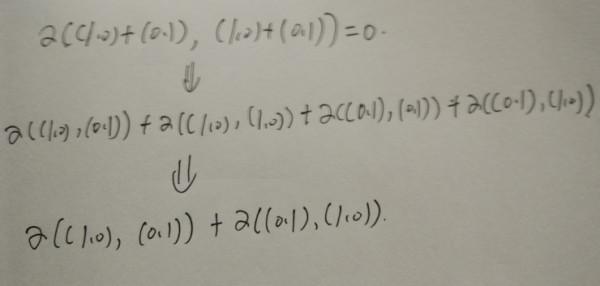
实际通过加法的线性映射,我们可以得到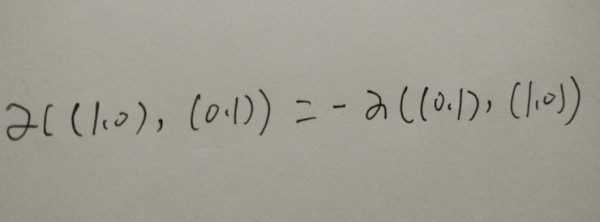
这像不像把矩阵[[1,0],[0,1]]的上下两行交换,所得到矩阵的行列式是原矩阵行列式的相反数。
行列式
现在我们假设用平面内的任意两个矢量所张成的平行四边形的面积,现在用公式来进行表示,好比两个矢量(a,0),(0,d)组成的长方形面积减去两个矢量(0,b),(c,0)组成的长方形面积,注意:减去是因为
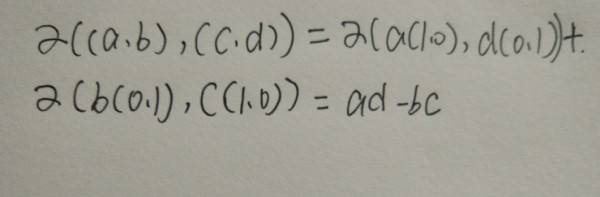
在这里,其实我们不难看到,所谓的面积其实就是一个2*2的矩阵的行列式:
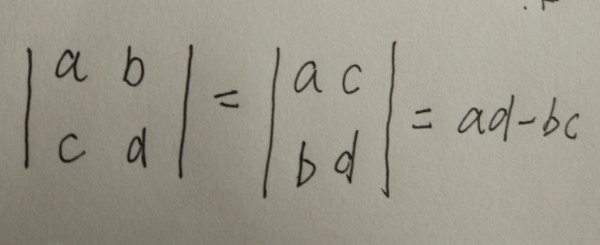
其实在这里,我们可以把各种维度所代表的东西来总结下,二维所代表的是平面内的面积,三维自然而然其实就是三维空间内的体积,四维其实就是四维空间内的超体积.依次类推.
秩
A是一个N*N的矩阵,a向量是列向量,V是N维体的体积:
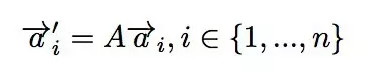
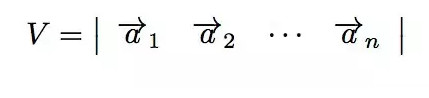
N维体的体积是(注意到,第二个等式实际上说明了几何意义是如何定义矩阵乘法的,也就是NN矩阵A和另外一个N个列向量组成的NN矩阵的乘法):
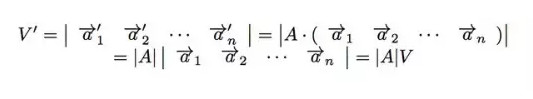
A的行列式如果不为零,则代表这个变换后,N维体的体积不是NULL。又结合线性无关与体积的性质,我们可以说:
如果A的行列式不为零,那么A可以把一组线性无关的矢量,映射成一组新的,线性无关的矢量;A是可逆的(一对一的映射,保真映射,KERNEL是{0})
如果A的行列式为零,那么A就会把一组线性无关的矢量,映射成一组线性相关的矢量
如果A的行列式为负数,那么A将会改变原N维体体积的朝向。
注意:从线性无关到线性相关,其中丢失了部分信息(例如坍缩成共线或者共面)。
比如:一个秩为2为3*3的矩阵A,因为秩小于3,那么任何一个3维六面体经过他的变化后,体积变为0,退化一个面,但是仍然存在一个面积不为0的面,在变换以后还是一个非零面积的面