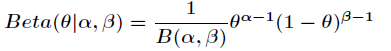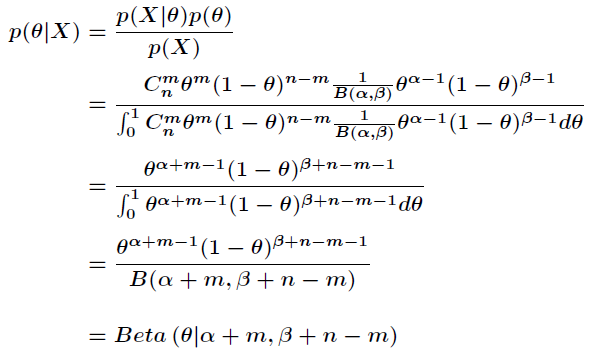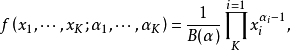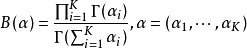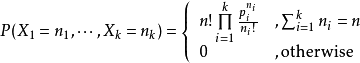常用的概率分布及其相互之间的联系与区别

二项式分布

二项实验：结果为0，1的集合，比如说美国大选，假设只有两名候选人的情况且不可以弃权的情况下，选特朗普为1，选希拉里为0。再比如说种子的发芽率实验，发芽为1，不发芽为0。
定义：
（1）整个实验由n次相同的实验组成。
（2）结果非0即1
（3）在一次实验中成功的概率为 $\pi$ ,且在不同的单次实验中保持不变
（4）各次实验为独立实验
（5）随机变量 $k$ 是在 $n$ 次实验中观测到的成功的次数。
计算公式：

P (X = k) = C k n π k (1 - π) n - k = n ! k ! ( n - k ) ! π k (1 - π) n - k

$P(X=k)=C_n^k\pi^k(1-\pi)^{n-k}=\frac{n!}{k!(n-k)!}\pi^k(1-\pi)^{n-k}$

P(k) $P(k)$ 是在

n $n$ 次实验中，当单次成功概率为

π $\pi$ 时，成功

k $k$ 次的概率。
记做：

X∼B(n,π) $X \sim B(n,\pi)$
均值:

μ=nπ $\mu=n\pi$
变准差:

σ=nπ(1−π)−−−−−−−−√ $\sigma=\sqrt{ n\pi(1-\pi)}$
举例：
种子发芽实验，

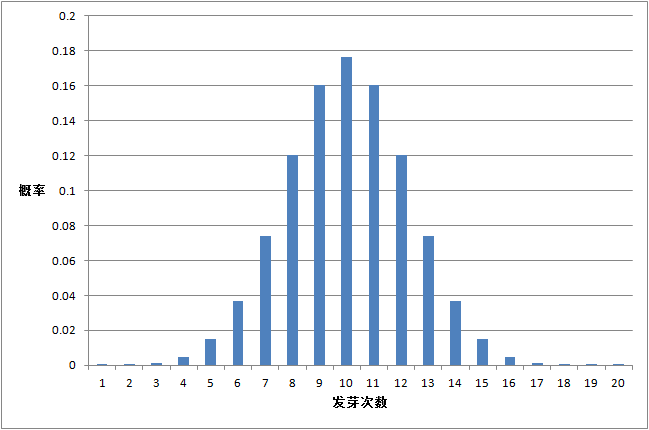
n=20 $n=20$ ，

π=0.5 $\pi=0.5$
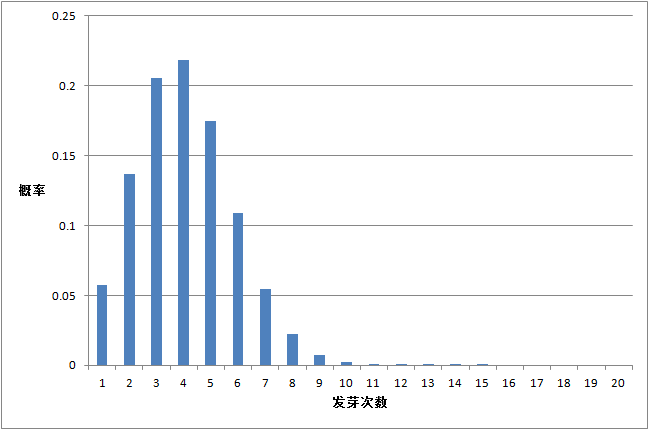
这里写图片描述

种子发芽实验，

n=20 $n=20$ ，

π=0.2 $\pi=0.2$
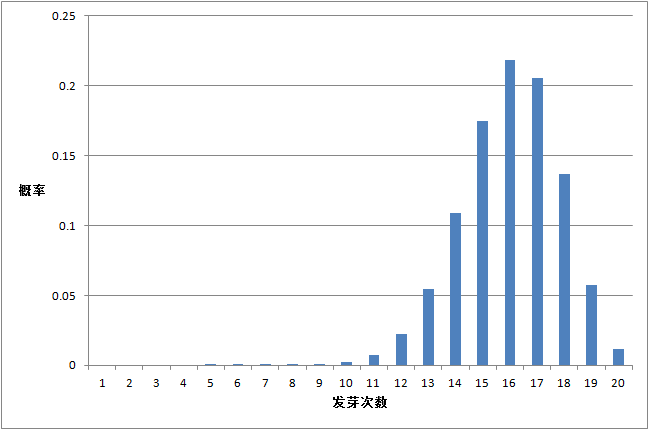
这里写图片描述

种子发芽实验，

n=20 $n=20$ ，

π=0.8 $\pi=0.8$
这里写图片描述

由上面三个图的对比我们可以看出：
只有在成功概率

π=0.5 $\pi=0.5$ 时候，是对称分布。其它的都是非对称的。最大值出现在均值的位置，离均值越远，出现的概率越小。

泊松分布

$~~~~~~~$ 假设我们现在要估计某个路口一小时经过 $k$ 辆车的概率，第一步我们需要先大量的观察一段时间，获得一个一小时内通过汽车数量的期望 $λ$ 。
$~~~~~~~$ 然后我们把一小时分为60分钟，同时假设每一分钟要么经过一辆车，要么没有车，那么按照二项分布的式子：
$P(X=k)=C_k^{60}(\frac{λ}{60})^k(1−\frac{λ}{60})^{60−k}$
也就是说，期望除以60分钟（把一小时分成60份）获得每一分钟有一辆车经过的概率。
$~~~~~~~$ 但是很明显我们不能确保每分钟真的只过一辆，为了更加精确，我们可以把一小时继续分为3600秒或72000个半秒，也就是说分的越多份，越精确。如果我们这么一直分下去，我们就获得了泊松分布，也就是二项分布的极限情况。
$~~~~~~~$ 泊松分布可以由二项分布的极限得到，比较好的分析请参考公开课《可汗学院-统计学》。

$~~~~~~~$ 泊松分布可作为二项分布的极限而得到。一般的说，若 $X \sim B(n,\pi)$ ,其中 $n$ 很大， $\pi$ 很小，因而 $np=\lambda$ 不太大时， $X$ 的分布接近于泊松分布。

p (X = k) = λ k e - λ k !

$p(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}$

$~~~~~~~$ (1)Poisson分布是一种单参数的离散型分布，其参数为

λ $\lambda$ ，它表示单位时间或空间内某事件平均发生的次数

μ=λ $μ=\lambda$ ，又称强度参数。

$~~~~~~~$ (2)．Poisson分布的方差

σ2 $σ^2$ 与平均数

λ $\lambda$ 相等，即

σ2=λ $σ^2=\lambda$

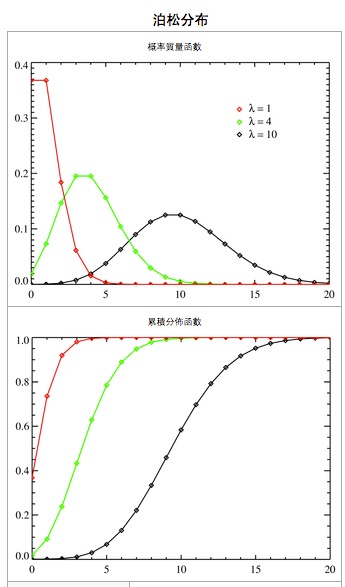
$~~~~~~~$ (3)Poisson分布是非对称性的，在

μ $μ$ 不大时呈偏态分布，随着

μ $μ$ 的增大，迅速接近正态分布。一般来说，当

μ $μ$ =20时，可以认为近似正态分布，Poisson分布资料可按正态分布处理。

这里写图片描述

$~~~~~~~$ 实验结果满足泊松分布的实验即为泊松过程。泊松过程把离散的伯努利过程变得连续化了。泊松过程需要满足以下三个性质：
$~~~~~~~$ 1. 在任意单位时间长度内，到达率是稳定的。对应于无穷次抛硬币的例子，我们相当于把一个单位时间分割成了无穷次抛硬币的实验，每次实验产生正面的概率都是一样的（为 $\lambda/n$ ），而在这无穷个抛硬币实验之后（即一个单位时间之后）我们期望能抛出 $\lambda$ 个正面的硬币。这个性质类比于在有限次抛硬币（二次分布）的例子中保证了每次掷出硬币为正面的概率都为 $\pi$ 。
$~~~~~~~$ 2. 未来的实验结果与过去的实验结果无关。对应于无穷次抛硬币的例子，之前不管抛出了多少个正面和反面的硬币，都不会影响之后硬币出现的结果。
$~~~~~~~$ 3. 在极小的一段时间内，有1次到达的概率非常小**，没有到达的概率非常大。对应于无穷次抛硬币的例子，我们发现硬币朝上的概率 $\pi=\lambda/n$ 趋向于0。
$~~~~~~~$ 更多关于泊松过程和泊松分布过程的例子，可参考http://maider.blog.sohu.com/304621504.html。

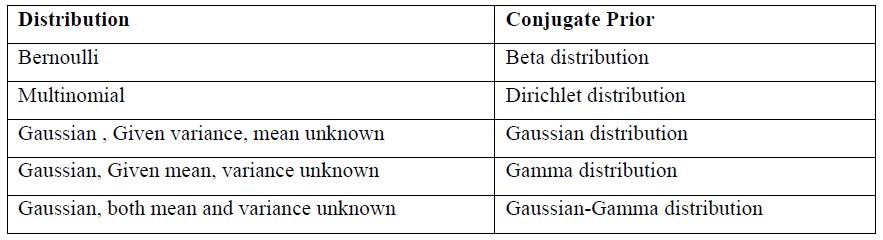
贝塔分布

共轭先验

$~~~~~~~$ 这个问题不是很容易理解，先从大家都知道的贝叶斯公式入手吧。

p (θ | X) = p ( X | θ ) p ( θ ) p ( X )

$p(\theta|X)=\frac{p(X|\theta)p(\theta)}{p(X)}$
我们要计算 后验概率

p(θ|X) $p(\theta|X)$ ,

p(θ) $p(\theta)$ 是事先计算好的已知 先验概率。

p(X|θ) $p(X|\theta)$ 叫做 似然概率。

$~~~~~~~$ 如果我们想计算得出的 后验概率

p(θ|X) $p(\theta|X)$ 和已知 先验概率

p(θ) $p(\theta)$ 具备同样的概率分布，那么显然需要 似然概率

p(X|θ) $p(X|\theta)$ 满足特殊的形式。

$~~~~~~~$ 数学家就把这种关系定义为“先验概率

p(θ) $p(\theta)$ 叫做似然概率

p(X|θ) $p(X|\theta)$ 的共轭先验。”，满足这个定义后， 后验概率

p(θ|X) $p(\theta|X)$ 和已知 先验概率

p(θ) $p(\theta)$ 就具备了同样的概率分布。

$~~~~~~~$ 下面以二项式分布和贝塔分布为例来说明：

$~~~~~~~$ 假设 先验概率

p(θ) $p(\theta)$ 为贝塔分布：
这里写图片描述

$~~~~~~~$ 上述贝塔分布是似然概率

p(X|θ) $p(X|\theta)$ 为二项式分布的“共轭先验”，证明如下：
这里写图片描述

$~~~~~~~$ 可以看出：神奇的是后验概率和先验概率具备相同类型的分布，即贝塔分布，因此上述假设是成立的，即“先验概率贝塔分布是似然概率为二项式分布的“共轭先验””。

$~~~~~~~$ 共轭先验的更多探讨：
$~~~~~~~$ 共轭先验在贝叶斯学习和LDA主题模型中是比较重要概念。
$~~~~~~~$ 为了加深对它的重要性的理解，下面重复说明:
$~~~~~~~$ PRML第68页说：“We shall see that an import role is played by conjugate priors, that lead to posterior distributions having the same functional form as the prior , and that therefore lead to a greatly simplified Bayesian analysis.”
$~~~~~~~$ 我们看到，共轭先验在贝叶斯推理中具有重要意义，它使得后验分布和先验具有相同的函数形式。
$~~~~~~~$ 使得贝叶斯推理更加方便，比如在Sequential Bayesian inference（连续贝叶斯推理）中，得到一个observation之后，可以算出一个posterior（后验）。由于选取的是Conjugate prior共轭先验，因此后验和原来先验的形式一样，可以把该后验当做新的先验，用于下一次observation，然后继续迭代。
$~~~~~~~$ 除了二项式分布和贝塔分布外，还存在另外一些先验分布及共轭分布，尤其是多项式分布和狄利克雷分布在主题模型LDA中有重要的应用，后面会详细说。
这里写图片描述

多项式分布

$~~~~~~~$ 多项式分布（Multinomial Distribution）是二项式分布的推广。
$~~~~~~~$ 把二项分布推广至多个（大于2）互斥事件的发生次数，就得到了多项分布。比如扔骰子，不同于扔硬币，骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是1/6（对应 $p_1~p_6$ ,它们的值不一定都是1/6，只要和为1且互斥即可，比如一个形状不规则的骰子），重复扔n次，点数1~6的出现次数分别为( $n_1,x_2,x_3,x_4,x_5,x_6$ )时的概率是多少？其中 $\sum_{i=1}^6x_i= n$ ”。这就是一个多项式分布问题。
$~~~~~~~$ 某随机实验如果有 $k$ 个可能结局 $A_1、A_2、…、A_k$ ，分别将他们的出现次数记为随机变量 $X_1、X_2、…、X_k$ ，它们的概率分布分别是 $p_1，p_2，…，p_k$ ，那么在 $n$ 次采样的总结果中， $A_1$ 出现 $n_1$ 次、 $A_2$ 出现 $n_2$ 次、…、 $A_k$ 出现 $n_k$ 次的这种事件的出现概率 $P$ 有下面公式：
$~~~~~~~$ $~~~~~~~$ $~~~~~~~$ $~~~~~~~$ $~~~~~~~$ 这里写图片描述

扫描二维码关注公众号，回复： 3851312 查看本文章

狄利克雷分布

$~~~~~~~$ 狄利克雷分布是一组连续多变量概率分布，Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙.
$~~~~~~~$ 贝塔分布是二项分布的共轭先验分布，那么狄利克雷分布就是多项式分布的共轭先验分布。
$~~~~~~~$ 狄利克雷分布常作为贝叶斯统计的先验概率。当狄利克雷分布维度趋向无限时，便成为狄利克雷过程（Dirichlet process）。
$~~~~~~~$ 　狄利克雷分布奠定了狄利克雷过程的基础，被广泛应用于自然语言处理特别是主题模型（topic model）的研究。
$~~~~~~~$ K阶狄利克雷分布的概率密度函数表示为如下形式：
$~~~~~~~$ 这里写图片描述
$~~~~~~~$ 归一化常数为对变量Beta函数，可以用Gamma函数来表示：
$~~~~~~~$
$~~~~~~~$ Dirichlet分布其实也是采样出一个值（向量）,从这个意义上来说,它其实和其它分布并无太大不同?那为什么大家都说Dirichlet分布式分布的分布呢?因为Dirichlet分布出现的场景,总是用于生成别的分布（更确切地说,总是用于生成多项式分布）
$~~~~~~~$ Dirichlet分布得到的向量各个分量的和是1,这个向量可以作为Multinomial分布的参数,所以我们说Dirichlet能够生成Multinomial分布,也就是分布的分布.
$~~~~~~~$ Dirichlet分布和Multinomial分布式共轭的,Dirichlet作为先验,Multinomial作为似然,那么后验也是Dirichlet分布.所以Dirichlet和Multinomial这个组合总是经常被使用,Dirichlet分布在这里的角色就是分布的分布（Multinomial分布的分布）.
$~~~~~~~$
$~~~~~~~$
$~~~~~~~$

正态分布

t分布

$~~~~~~~$ 在概率论和统计学中，学生t-分布（Student’s t-distribution）经常应用在对呈正态分布的总体的均值进行估计。它是对两个样本均值差异进行显著性测试的学生t测定的基础。T检验改进了Z检验，不论样本数量大或小皆可应用。在样本数量大（超过120等）时，可以应用Z检验，但Z检验用在小的样本会产生很大的误差，因此样本很小的情况下得改用学生t检验。在数据有三组以上时，因为误差无法压低，此时可以用变异数分析代替学生t检验。
$~~~~~~~$ 当母群体的标准差是未知的但却又需要估计时，我们可以运用学生t-分布。
$~~~~~~~$ 学生t-分布可简称为t分布。其推导由威廉·戈塞于1908年首先发表，当时他还在都柏林的健力士酿酒厂工作。因为不能以他本人的名义发表，所以论文使用了学生（Student）这一笔名。之后t检验以及相关理论经由罗纳德·费雪的工作发扬光大，而正是他将此分布称为学生分布。

卡方分布

高斯分布

F分布

本文在编写的过程中参考（或部分拷贝）了以下文章，在此表示非常感谢，本着自由交流与学习的目的，如果有所侵犯，绝非作者本意，请联系作者，会及时改正之。
参考文章：
（1）贝叶斯学习及共轭先验：http://blog.csdn.net/acdreamers/article/details/45026459
（2）Polly Study PRIS CSDN 《Conjugate prior-共轭先验的解释》http://blog.csdn.net/polly_yang/article/details/8250161
（3）The Dirichlet Distribution 狄利克雷分布 (PRML 2.2.1) http://www.xperseverance.net/blogs/2012/03/510/