ML—线性回归系列（一）—线性回归

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/zhangzhengyi03539/article/details/50035265

Andrew Zhang
Tianjin Key Laboratory of Cognitive Computing and Application
Tianjin University
Nov 25, 2015

本来以为线性回归是一个特简单的东西，最近遇到很多基于线性回归的东西，才意识到我的无知。为了记录最近的学习历程，还是从线性回归开始系统总结一下吧。

一、线性回归
在实际问题中，在考虑变量$y$与另外一些变量$x_1,x_2,...,x_n$ 之间关系的时候，为了简化往往考虑线性模型
$h_{\theta}(x)=\theta_0+\theta_1x_1+...+\theta_nx_n={\theta^Tx} \tag{1-1}$
其中$x_0=1$.

接下来，目标就是对于训练数据集$(x^i,y^i),i=1,2,...,m$确定模型最合适的参数$\theta$。采用最小二乘法，定义损失函数
$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2 \tag{1-2}$
这里采用最小二乘是因为最小二乘得到的参数$\theta$优效性最好(在所有的线性无偏估计量里面方差最小).

二、梯度下降法
最小二乘是无约束优化的凸问题，属于最简单的凸优化问题，有很多的数值求解的方法，参考参考博客[1]。本文介绍梯度下降法求解最小二乘优化问题。
在梯度法中参数$\theta$的更新规则为：
$\theta_j=\theta_j-\alpha\frac{d}{d\theta_j}J(\theta) \tag{2-1}$
其中$\alpha$ 为学习率，可以设定为常数，也可以采用一维搜索方法确定，具体可以查看参考博客[2]
$\frac{d}{d\theta_j}J(\theta)$
$=\frac{d}{d\theta_j}(\frac{1}{2}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$
$=\frac{1}{2}\sum_{i=1}^{m}{2\cdot(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_j^{(i)}}$
$=\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_j^{(i)}}$
$\tag{2-2}$
公式(2-2)带入公式(2-1)得到$\theta_j$的更新规则为：
$\theta_j=\theta_j-\alpha\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_j^{(i)}} \tag{2-3}$
采用公式(2-3)的方法被称为批梯度下降法。由于批梯度下降法对与每一次$\theta$的更新需要计算所有的样本，不利于在线计算，因此一般使用如下公式(2-4)所示的随机梯度下降法(理解的时候只需要每次对参数进行更新迭代的时候假设只有一个样本即可)：
$\theta_j=\theta_j-\alpha{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_j^{(i)}} \tag{2-4}$
并且往往公式(2-4)的收敛效率要远远高于(2-3)，可以更早的达到收敛。

三、最小二乘的概率解释
在参考博客3中说了线性规划的最小二乘属于广义线性模型，并进行了推导，得到了
$p(y|x,\theta)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(y-\theta^Tx)^2) \tag{3-1}$
在这里我们看一种更简单点的解释，假设输出y与输入x服从如下等式
$y^{(i)}=\theta ^T x^{(i)}+\epsilon^{(i)} \tag{3-2}$
由于对于取样的每个样本都是独立同分布的，假设误差项$\epsilon^{(i)}$~$N(0,\sigma^2)$
则对于每一个取样样本有
$p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi }\sigma}exp(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}) \tag{3-3}$
由公式(3-2)得$\epsilon^{(i)}=y^{(i)}-\theta ^T x^{(i)}$带入公式(3-3)得到
$p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta ^T x^{(i)})^2}{2\sigma^2}) \tag{3-3}$
公式(3-3)便是样本$(x^{(i)},y^{(i)})$的先验概率公式。接下来就是统计学里面的参数估计问题了。求解似然函数极大化似然函数即可。
似然函数为：
$L(\theta)=\prod_{i=1}^{m}{p(y^{(i)}|x^{(i)};\theta)} \tag{3-4}$
对数似然函数为：
$l(\theta)=\log L(\theta)=\log \prod_{i=1}^{m}{\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta ^T x^{(i)})^2}{2\sigma^2})} \tag{3-5}$
化简公式(3-5)得
$l(\theta)=m\log \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{2\sigma^2}\sum_{i=1}^{m}{(y^{(i)}-\theta ^T x^{(i)})^2} \tag{3-6}$
刨除公式(3-6)的常数部分，极大化似然函数(3-6)等价于极小化其中的$\sum_{i=1}^{m}{(y^{(i)}-\theta ^T x^{(i)})^2}$部分，即文章开头所说的最小二乘部分的$J(\theta)$（公式(1-2)）。

四、矩阵求解最小二乘
把所有的样本$(x^{(i)},y^{(i)})$用矩阵的形式表示，可以写成如下的形式
$Y=X\theta+\epsilon \tag{4-1}$
目标是求解$\theta$是的$\epsilon^T\epsilon$最小。令
$S(\theta)=\epsilon^T\epsilon=(Y-X\theta)^T(Y-X\theta) \tag{4-2}$
$\frac{d}{d\theta}S(\theta)=2X^T(Y-X\theta)=0 \tag{4-3}$
即$X^TX\theta=X^TY$
这里假设$X=(X_1,X_2,...,X_n)$中的列向量都是线性无关的(如果不满足就先进行一步冗余特征删除)，并且$m>>n$，即$rank(X)=n$，那么$rank(X^TX)=rank(X)=n$，即$X^TX$可逆。
所以有最小二乘的矩阵形式解—公式(4-4)
$\theta=(X^TX)^{-1}X^TY \tag{4-4}$

五、矩阵求解的SVD解释
在第四部分已经得到$\theta=(X^TX)^{-1}X^TY$。这一部分利用SVD知识初探线性回归几何意义(主要为岭回归铺垫)。
假设$X \in R^{m\times n}$的SVD分解为
$X=U\Sigma V^T \tag{5-1}$
其中$U=(u_1,u_2,...,u_n)\in R^{m\times n}$,$\Sigma=diag(\sigma_1,\sigma_2,...,\sigma_n) \in R^{n\times n}$,$V=(v_1,v_2,...,v_n) \in R^{n\times n}$，$v_1,v_2,...,v_n$是原始样本空间的一组标准正交基，$u_1,u_2,...,u_n$分别是原始样本在这组基下的正交标准化坐标。
$X^TX=(U\Sigma V^T)^TU\Sigma V^T=V\Sigma U^TU\Sigma V^T=V\Sigma^2V^T \tag{5-2}$
带入公式4-4可得
$\theta=(V\Sigma^2V^T)^{-1}(U\Sigma V^T)^TY=V\Sigma^{-1}U^TY=\sum_{i=1}^{n}{\frac{1}{\sigma_i}v_iu_i^TY} \tag{5-3}$
对于公式5-2，可以发现想要得到矩阵$X$的SVD分解，只需要求解矩阵$X^TX$的特征值和特征向量就能得到$\Sigma和V$，然后根据$u_i=Xv_i$即可得到矩阵$U$。
并且，根据SVD的几何意义，我们知道$z=Xv_1$实际上是在原始空间求得新基$v_1$使得矩阵$X$在新基上坐标方差$Var(z_1)$最大。根据SVD的知识有有$Var(z_i)=\frac{\sigma_i^2}{N},Xv_i=u_i\sigma_i$这里可见SVD实际上是广义的PCA。

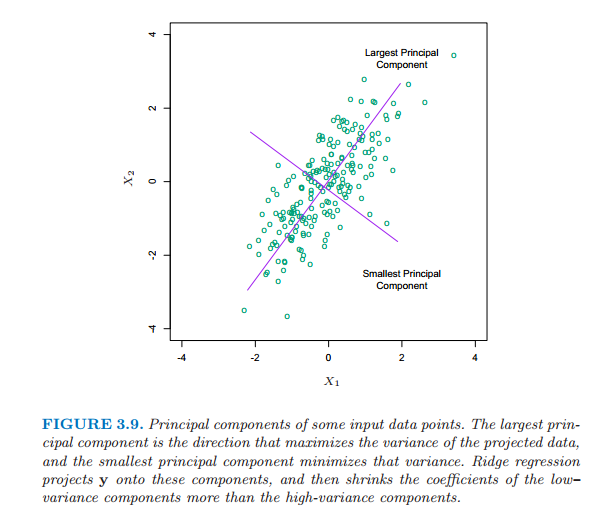
六、参考博客
1、最优化方法—无约束极值问题的解法
(http://blog.csdn.net/zhangzhengyi03539/article/details/49705305)
2、最优化方法—一维搜索
(http://blog.csdn.net/zhangzhengyi03539/article/details/49704893)
3、ML—广义线性模型(GLM)
(http://blog.csdn.net/zhangzhengyi03539/article/details/46834379)
4、你应该知道的7种回归技术