ML学习笔记——线性回归

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/qq_27124771/article/details/81353781

有监督学习分为回归和分类：
- 回归：通过数据最终预测出来一个值（例如，去银行贷款，银行根据你的年龄与工资预测出可以给你贷款多少钱）
- 分类：通过数据最终预测出来类别（例如，去银行贷款，银行根据你的年龄与工资判断能否给你贷款）

而线性回归是找到最合适的一条线（想象一个高维）来最好的拟合数据点。

举个例子，现有贷款人工资与年龄数据，还有与之对应的银行贷款金额，需要预测银行会贷款给自己多少钱。

工资	年龄	额度
4000	25	20000
8000	30	70000
5000	28	35000

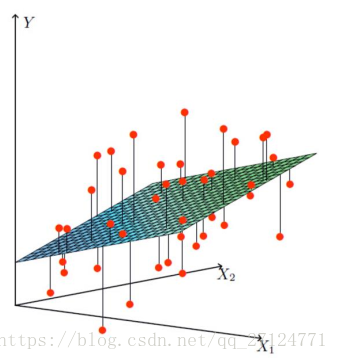
我们可以把问题抽象成如何找到最合适的一条线来最好的拟合数据点，如下图，$X_1，X_2$是两个特征（工资与年龄），$Y$是银行的贷款额度。

假设$\theta_1$是年龄参数，$\theta_2$是工资参数，则拟合的平面可以表示为：

$$h_\theta(x)=\theta_0 + \theta_1x_1+\theta_2x_2$$

其中$\theta_0$是偏置项，为了便于计算，通常将其整合成矩阵形式，添加一列$x_0$属性，全部置为1，使得等式成立：

$$h_\theta(x) =\sum_{i=0} ^ {n} \theta_ix_i = \theta^Tx$$

平面的表达式有了，但是我们不能保证每一个数据点都在这个平面上吧，所以真实值和预测值之间肯定是要存在差异的（用$\varepsilon$来表示误差），对每一个样本就存在：

$$y^{(i)}=\theta^Tx^{(i)}+\varepsilon^{(i)}$$

【假设】每一个样本的误差$\varepsilon^{(i)}$都是独立并且具有相同的分布，并且服从均值为0方差为$\theta^2$的高斯分布

解释

• 独立：张三和李四一起来贷款，他俩没关系

• 同分布：他俩都来的是相同的一家银行

• 高斯分布：银行可能会多给，也可能会少给，但是绝大多数情况这个浮动不会太大，极小情况下浮动会比较大，符合正常情况

由于误差服从均值为0的高斯分布，可得公式：

$$p(\varepsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\varepsilon^{(i)})^2}{2\sigma^2})$$

将$y^{(i)}=\theta^Tx^{(i)}+\varepsilon^{(i)}$ 带入此公式可得：

$$p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})$$

似然函数：根据样本估计参数值，什么样的参数跟我们的数据组合后成为真实值的可能性最大，预测值成为真实值的概率越大越好。

$$L(\theta)=\prod_ {i=1}^m p(y^{(i)}|x^{(i)};\theta) = \prod_ {i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})$$

似然函数中的乘法难解，所以将其转换为对数似然，变成加法更容易解出。

$$\begin{align*} log L(\theta) &= \prod_ {i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}) \\ &= \sum_{i=1} ^ {m}log \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}) \\ &= mlog\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2}\sum_{i=1} ^ {m}(y^{(i)}-\theta^Tx^{(i)})^2 \end{align*}$$

我们的目标是让似然函数越大越好，上式中，被减数是恒正的，所以要让减数越小越好，可得目标函数（最小二乘法）：

$$\begin{align*} J(\theta)&=\frac{1}{2}\sum_{i=1} ^ {m}(y^{(i)}-\theta^Tx^{(i)})^2\\ &=\frac{1}{2}\sum_{i=1} ^ {m}(h_\theta (x^{(i)})-y^{(i)})^2\\ &=\frac{1}{2}(X\theta-y)^T(X\theta-y) \end{align*}$$

现在的任务是让目标函数越小越好，那么$\theta$取什么的时候目标函数最小呢？$\theta$应该是极小值或最小值点，所以对目标函数进行求偏导，使偏导等于0。那为什么一定是极小值点呢，这涉及到凸优化的概念，普遍认为我们的函数都是凸函数。

$$\begin{align*} \nabla_\Theta J(\Theta)&=\nabla_\Theta\lgroup\frac{1}{2}(X\theta -y)^T(X\theta -y)\rgroup =\nabla_\Theta\lgroup\frac{1}{2}(\theta^TX^T)(X\theta -y)\rgroup \\ &=\nabla_\Theta\lgroup\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty)(X\theta -y)\rgroup \\ &=\frac{1}{2}(2X^TX\theta-X^Ty-(y^TX)^T)\\&=X^TX\theta-X^Ty \end{align*}$$

另偏导为零，可得下面的公式，这时基于数据可以计算出$\theta$值。

$$\theta = (X^TX)^{-1}X^Ty$$

评估方法

最常用的评估项$R^2$：

$$1-\frac{\sum_{i=1}^{m}(\hat{y_i}-y_i)^2}{\sum_{i=1}^{m}(y_i-\bar{y})^2}$$

分子为残差平方和，分母为类似方差项，$R^2$的取值越接近于1模型拟合的越好