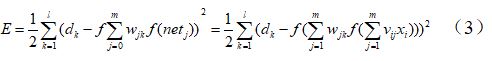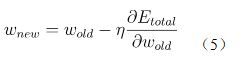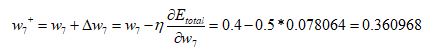在这里我们只做总结梳理,具体的证明我们并不涉及,只要掌握原理,并为我们所用即可。
一、感知器——单个神经元

在说明神经网络之前,先介绍一下神经网络的基础计算单元——神经元,也是一直沿用至今的“M-P神经元模型”。在这个模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”处理以产生神经元的输出,两层神经元组成感知器。

上图就是一个简单的感知器,蓝色是输入的样本,g(z)是激活函数,z=x1*w1+…,a=g(z)
这个东西可以用来干什么呢?我们可以令b=-30,w1=20,w2=20,此时限制输入的x1和x2为0或者1,激活函数为sigmoid函数:
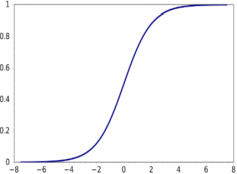
上图为sigmoid函数图像,可以看出当x很大时,此函数趋于1,当x很小时,此函数趋于0,写出真值表,可以发现这个感知器完成了一个逻辑与的操作。

将参数修改为b=-10,w1=20,w2=20,此时感知器又完成了一个逻辑或的操作,真值表就不写了,也就是说改变这些圆圈圈之间的传递参数,可以使这个感知器完成逻辑或和逻辑与的操作。当然对一个输入取非也不会有问题(b=10,w1=-20)。因此,我们可以改变连接参数,从而使感知器完成与、或、非的操作。
感知器的学习规则可以表示如下:
其中成为学习率。若感知器对训练样例预测正确,则感知器不会发生变化,否则将根据错误的程度进行权重调整。因此,我们可以改变连接参数,从而使感知器完成与、或、非的操作。
二、多层感知器——人工神经网络
在单层感知器的输入部分和输出层之间加入一层或多层处理单元,就构成了二层或多层感知器。在感知器模型中,只允许某一层的连接权值可调,这是因为无法知道网络隐层的神经元的理想输出,因而难以给出一个有效的多层感知器学习算法。多层感知器克服了单层感知器的许多缺点,原来一些单层感知器无法解决的问题,在多层感知器中就可以解决。例如,应用二层感知器就可以解决异或逻辑运算问题。常见的神经网络是形如下图所示的层级结构,每层神经元与下层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接,这样的神经网络结构通常称为“多层前馈神经网络”,其中输入层神经元神经元接受外界输入,隐层与输出层对信号进行加工,最后结果由输出层神经元输出。

这就是一个典型的神经网络,我们设为j层到j+1层的传递矩阵,从输入层(蓝色)到中间的第二层,就有:

同理,第二层到输出层:
![]()
注意这个神经网络的输出只有一个值而神经网络的输出可以有任意个,这里仅以此为例不再展开写,上边就是当已知每一层之间的系数矩阵时,神经网络求解的过程。

举个最简单的非线性问题之一:异或。

利用两层感知机可以实现异或的计算,但是如何求异或中间的权重w,是一个非常关键的问题,求得参数,既可以得到该问题的解。这里引申出BP算法来求解人工神经网络。
三、BP算法

BP算法基本分为这两个过程:
正向传播FP(求损失),在这个过程中,我们根据输入的样本,给定的初始化权重值W和偏置项的值b,计算最终输出值以及输出值与实际值之间的损失值,如果损失值不在给定的范围内则进行反向传播的过程;否则停止W,b的更新。
反向传播BP(回传误差),将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。
先简单说一下什么是梯度下降(SGD)。我们假设有一个凸函数如图所示,如何从随机的一点逐渐收敛到这个函数的最小值呢?
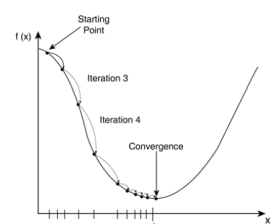
下边的伪代码就是梯度下降。当循环次数达到一定数量时,此时的x就非常接近f(x)的最小值了。
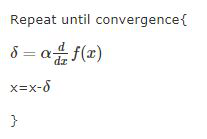
a是一个更新率,当a很小时梯度收敛的很慢,当a较大时梯度收敛的较快,当a过大时可能无法收敛,比如x减去一个很小的负值,函数值比原来距离正确的最小值点更远了。可见对于这样一个平滑的凸函数,迭代的步子会随着次数增加越迈越小,原因就是导数越来越小了。这样就会使得x逐渐逼近最小值点。
对于神经网络的损失函数,它不仅仅有一个参数,我们便需要求出损失函数对每个参数的偏导数,在最后统一进行参数更新后进行下一轮迭代。
神经网络系统使用正向传播求当前参数的损失,然后反向传播回传误差,根据误差信号迭代修正每层的权重。SGD算法(stochastic gradient descent)的第一步是随机初始化每一个参数。Stochastic的意思正是随机。通过这组随机的参数计算得到每一个神经元的输入输出值和损失函数后,就可以求损失函数对各个参数的偏导数了,梯度更新的那个delta就等于alpha*偏导数。
而BP算法则是用来求那一堆偏导数的,BP的意思是反向传播。就是把最后一层的误差反向传递回别的神经元,得到每一层的误差函数,从而解出偏导数。
输出层的误差求取规则如下:

隐含层误差的求取规则如下:

再更新输入层的权值,再递归更新权值,求得参数。
基本过程如下算法规则,求出参数:

举个例子:
各部分输入输出如图3所示, 下面进行各层误差计算.
输出层的误差(平方和误差,前面的1/2是为了后面的计算方便) 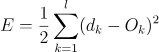 (1)
(1)
展开至隐层的误差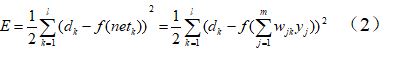
输入层误差
观察上式, 我们很容易看出只有(3)式和输入x有关。E有了,那么就很简单可以看出可以使用常用的随机梯度下降法(SGD)求解.也就是求解式子中的W和V,使得误差E最小。

设初始权重值w和偏置项b为:
w=(0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65)
b = (0.35,0.65)-->这里为了便于计算,假设从输入层到隐层之间, 隐层到输出层之间的偏置项b恒定.
1) FP计算过程
① 从输入层到隐层(其实这里的b可以看成一个特征)
h1 = w1*l1 + w2*l2 + b1*1 = 0.1*5 + 0.15*10 + 0.35*1 = 2.35
h2 = w3*l1 + w4*l2 + b1*1 = 0.2*5 + 0.25*10 + 0.35*1 = 3.85
h3 = w5*l1 + w6*l2 + b1*1 = 0.3*5 + 0.35*10 + 0.35*1 = 5.35
则各个回归值经过激活函数变换后的值为:
![]()
![]()
![]()
② 隐层到输出层
neto1 = outh1*w7 +outh2*w9 +outh3*w11+ b2*1= 2.35*0.4 + 3.85*0.5 +5.35 *0.6+0.65 = 2.10192
neto2 = outh1*w8 +outh2*w10 +outh3*w12 +b2*1= 2.35*0.45 + 3.85*0.55 +5.35 *0.65 +0.65= 2.24629
则经过激活函数变换得到:
outo1 = 0.89109 (真实值0.01) , outo2 = 0.90433 (真实值0.99)
此时的平方和误差为:
与真实值不符,需要进行BP反馈计算。
2) BP计算过程
这里的BP计算我们分为两个部分. ①隐层到输出层的参数W的更新 ②从输入层到隐层的参数W的更新.
在这里,我们主要讲述第一部分隐层到输出层的参数W的更新。

如图所示为从隐层到输出层的网络结构图。
首先,运用梯度下降法求解W7的值.
目标函数:![]() ,由于此时求解W7,所以只与有关,则此时的损失函数为:
,由于此时求解W7,所以只与有关,则此时的损失函数为:
![]()
可以看出, 为凸函数(开口向上), 有最小值且最小值在导数为0的点上。
又有 neto1 = outh1*w7 +outh2*w9 +outh3*w11+ b2*1, outo1 = f(o1)
则W7求偏导数得到:
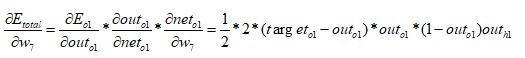
又有w的更新公式:
这样将上式带入W的更新公式(5)就可以求得更新后的W值。
最后,得到了W7的更新值为:
同理可以求得w9,w11,b2的更新值。
对于从输入层到隐层的参数W的更新,其实和从隐层到输出层的几乎一样,唯一不同的就是链式求导过程中的Etotal和outo1,outo2都有关系,这里就不展开解释了。
BP神经网络解决了神经网络中非常重要的问题,它解决了DNN中的隐层传递中的权重值的计算问题,极大地促进了神经网络的发展
参考文献:
https://blog.csdn.net/qq_32241189/article/details/80305566
https://www.cnblogs.com/asdfjkl/p/6159675.html
《机器学习》周志华