线性规划专题——SIMPLEX 单纯形算法（三）——示例、实现、注意点

版权声明：本文为博主jmh原创文章，未经博主允许不得转载。 https://blog.csdn.net/jmh1996/article/details/85011704

线性规划专题——SIMPLEX 单纯形算法（一）
线性规划专题——SIMPLEX 单纯形算法（二）

前面两篇博文已经把单纯形算法里面的核心思想给解释清楚了，主要是要认识到在线性规划里面的以下几点：

1. 目标函数的最优值一定在可行域的顶点取得。

2. 可行域的顶点对应这系数矩阵的一组基；系数矩阵的一组基也对应这一个可行域上的顶点

3. 顶点的转移是通过在旧的基本列里面加入新的列，同时为了保持rank一致，再从基本列里面删去一列。在转移的时候，重点就是要求出那个 $\vec \lambda$ 来，它其实是使得 $A\vec\lambda=0$ 的 $\vec \lambda$的解，只不过在解这个方程的时候，选择 $A$ 的那组旧的基本列来求解。

4. 单纯形法的终止条件是，添加任意的非基本列都不能改善目标函数，此时目标函数到达最小值。

OK,本博客来看看到底如何来用这个单纯形法来解线性规划。

一般，单纯形法会使用一个表格。使用表格来记录。我们来举几个例子。

再次使用如下记号来表示线性规划的松弛型：

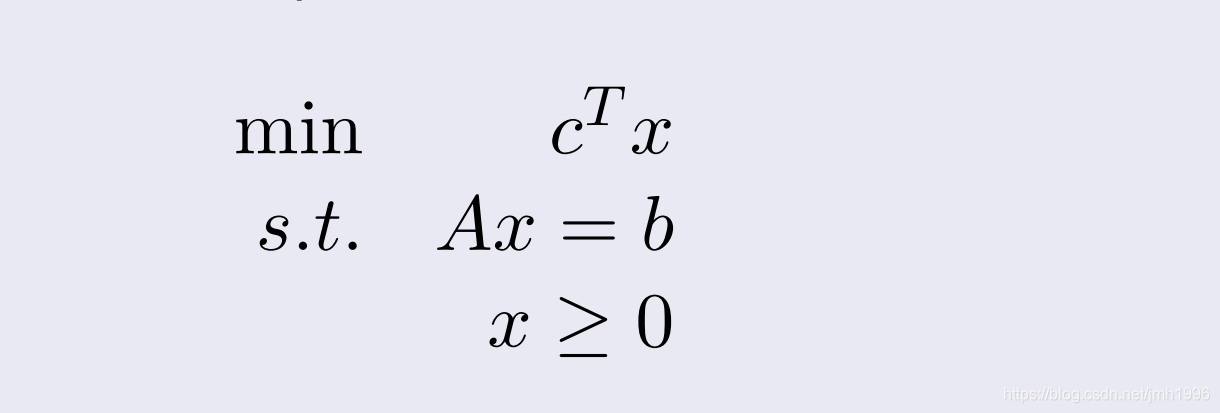
几个例子

例1

假设存在如下的线性规划：

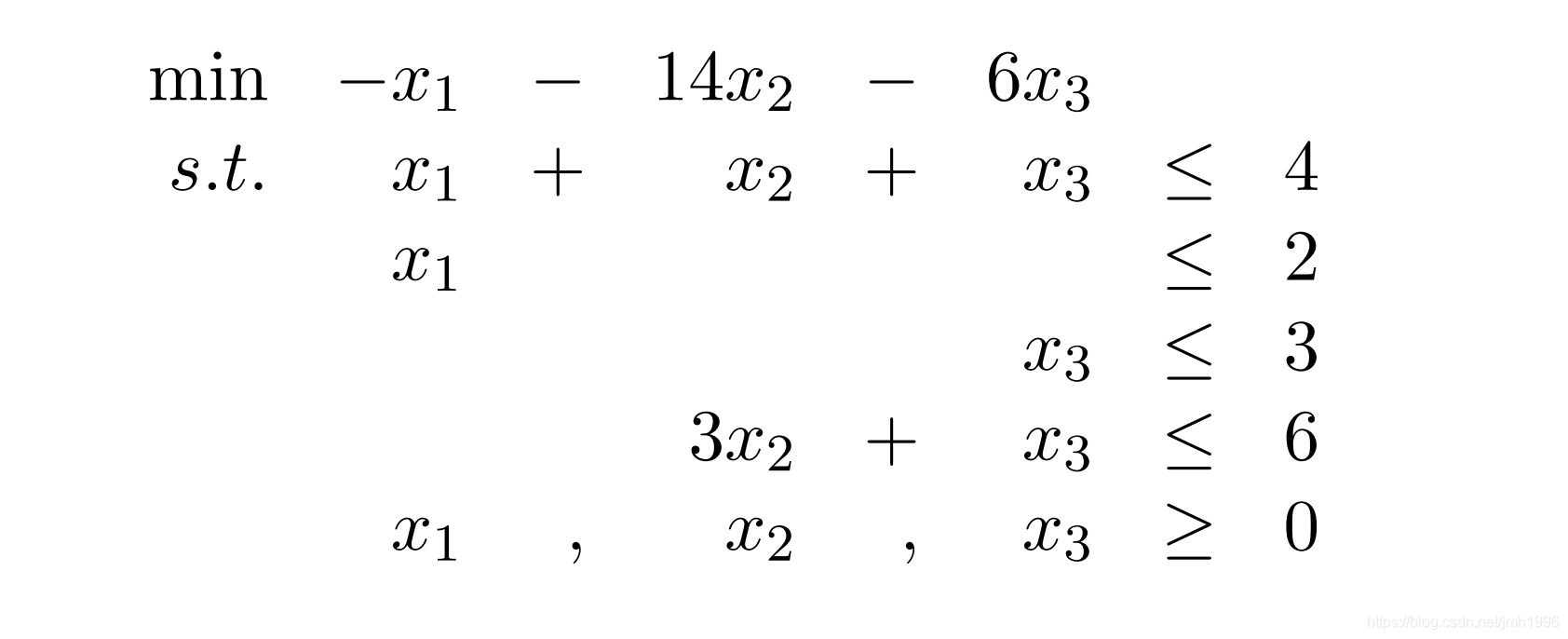
这是一个标准型的线性规划。我们添加松弛变量，得到松弛型：

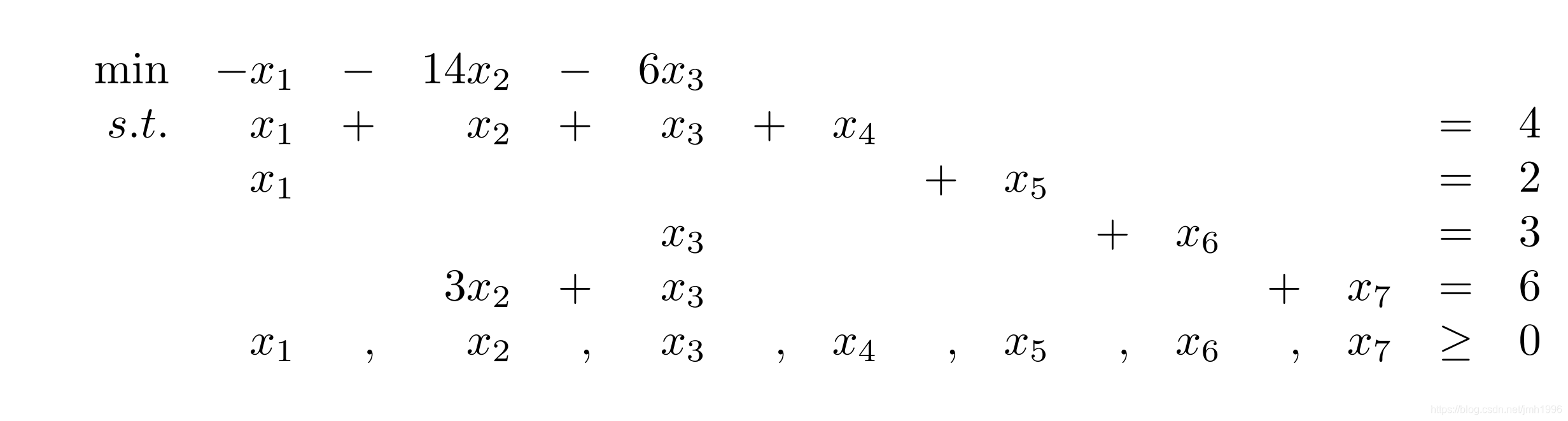
这个线性规划的右边的所有 $b_i$ 都是非负的，所以： $X=[0,0,0,4,2,3,6]$ 就是满足条件的一个顶点。

我们画出下面这个表格出来：

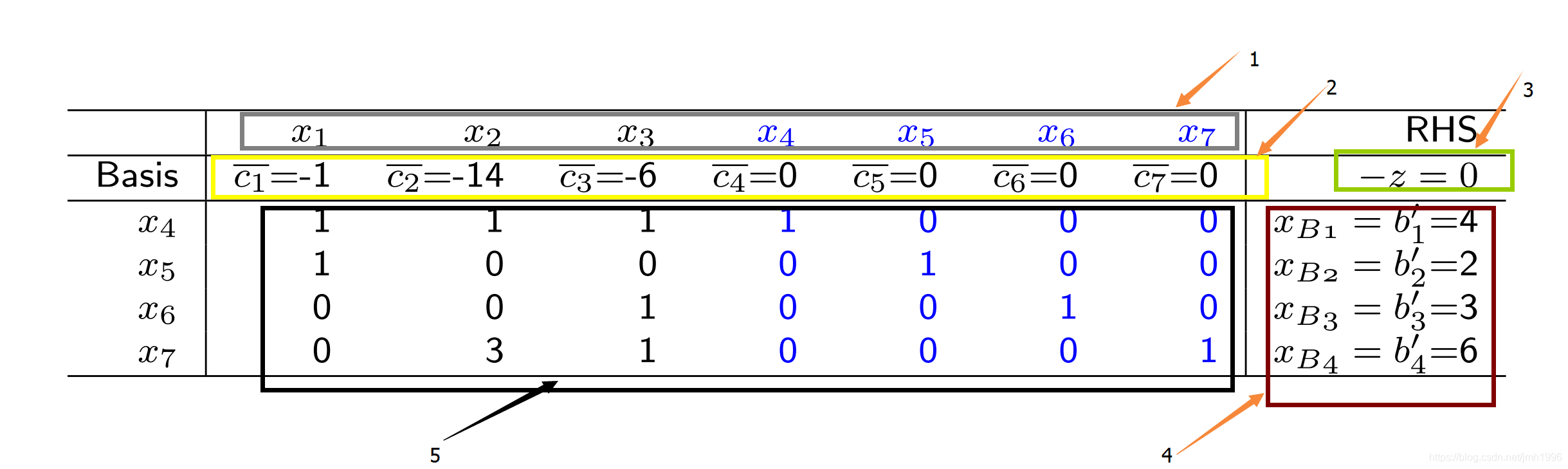
这个表格一共有5部分组成。
第1部分，表示各个变量。

第2部分，目标函数的各个系数，这些系数是与第一部分的变量是对应起来的。 $\overline c_i$ 与 $x_i$对应。

第3部分，当前得到的目标函数值的相反数。

第4部分，对应于 $AX=b$ 的 b，它其实表示了选定基本列后，基本列对应的 $x_i$的值，那些非基本列的 $x_j$ 全部为0。上面的表格说明 基本列是第4,5，6,7列，这组基对应的顶点是 $X=[0,0,0,4,2,3,6]$

第5部分，系数矩阵。 每一列与变量也是对应的，第i列表示第i个变量的系数列。

注意，我们需要始终保持基本列都是 $e_i$ , $e_i$是单位阵的第 $i$列。化成这种形式是为了方便的解方程和求 $\vec \lambda$。

怎么操作呢？
每次从第2部分中，选择一个负的 $\overline c_{i}$ ，负的意味着把 $c_i$对应的列添加进来以后，目标函数是会减少的。

例如，现在 $x_4,x_5,x_6,x_7$ 对应的列都是基本列，然后现在 $\overline c_1$ 是小于0的。那么，我们就想把这一列换到基本列去，然后把旧的基本列某一列给丢掉。

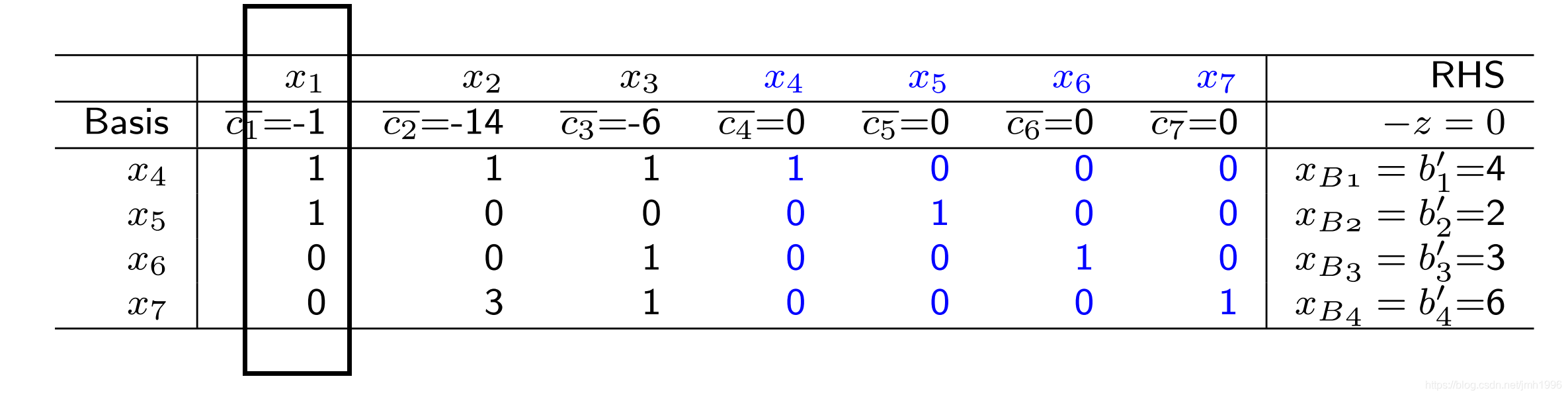
既然要换入第1列，那么我们就要解出 $\vec \lambda$来，也就是要用第4，5,6，7列去表示第1列。

我们发现第1列是 $[1,1,0,0]$，而基本列刚好是单位阵的列，所以第1列其实也就表明了如何用基本列去表出它。即我们可以很快的写出： $\vec \lambda=[-1,0,0,1,1,0,0]$.后面4个元素 就是第1列的4个元素，这得益于基本列是单位阵的列。

找到了 $\vec \lambda$,我们选择合适非负的 $\theta$,使得 $X'=X-\theta \vec \lambda$ 也是个顶点。为啥要选择非负的 $\theta$ 呢。
这是因为： $A\vec\lambda=\vec 0$，而 $AX=b$，于是 $AX'=AX-\theta A\vec\lambda=b$ 是满足第一个约束。

考虑到 $X'=X- \theta \vec \lambda$ 里面， $X=[0,0,0,4,2,3,6]$ 的每一项都是非负，而且是非基本列对应的项为0，第1列不是基本列，所以 $x_1$也是0。而 $\vec \lambda$ 出了第1项为-1，其他也全部非负。当 $\theta \leq 0$,那 $X'$的第1项 $x'_1=-\theta\lambda_1=\theta < 0$ 就不满足条件了。

所以得考虑非负的 $\theta$ 。
这个 $\theta$ 的取法是，用表格的第4部分的每一行的元素去对应除以第1列的元素，得到他们的最小非负的商。对于 $\frac{3}{0}$ 和 $\frac{6}{0}$ 的情况，记他们的商为正无穷。

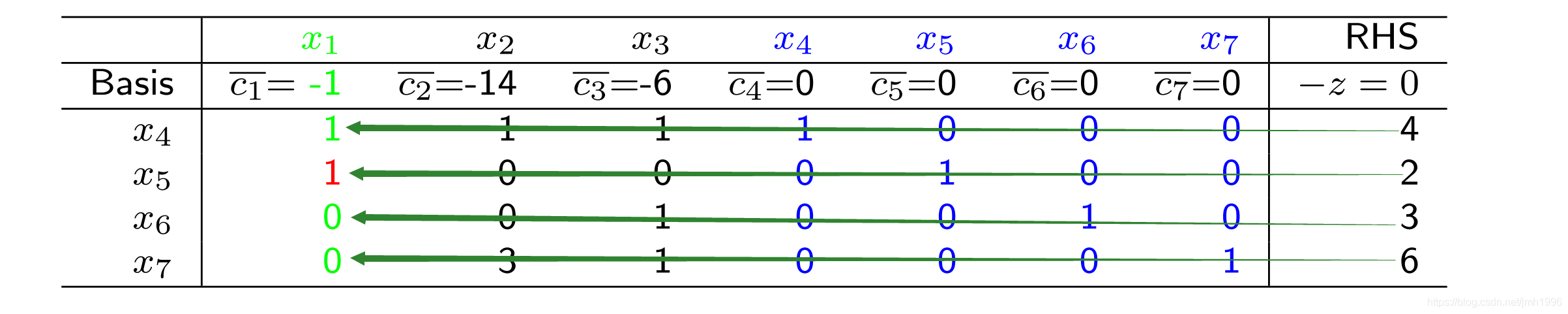
这样除下去，我们得到所有可能的 $\vec \theta$为 $[4,2,+\infty,+\infty]$，其中最小的是 $\theta_2=2$，于是选择 $\theta=2$，然后 现在 关键来了：以第1列的第2行为主元，通过高斯消元法，把第1列第2行的其他元都消掉，包括 $\overline c$那一行，消元的时候带着第4部分一起消。

经过处理后，我们得到：
变化后：

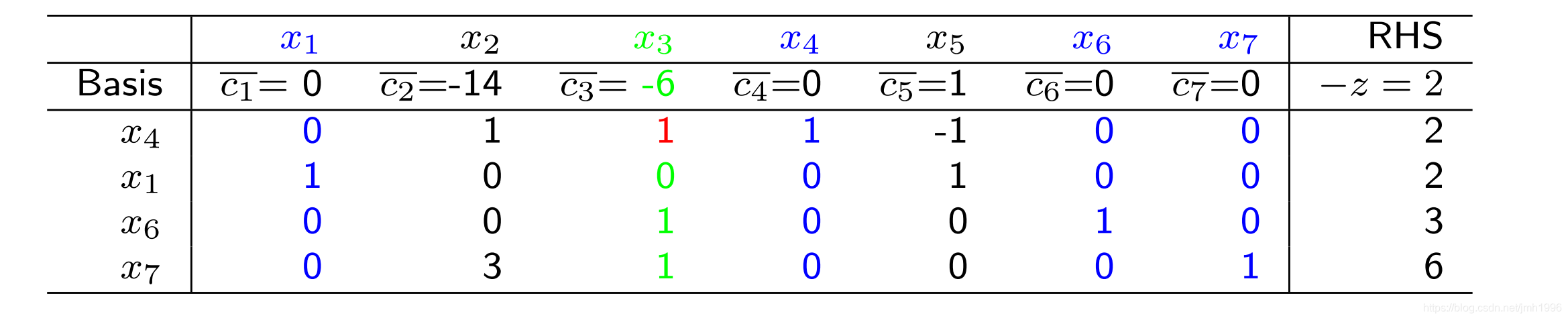
变化前：